1. Introduction to Sets

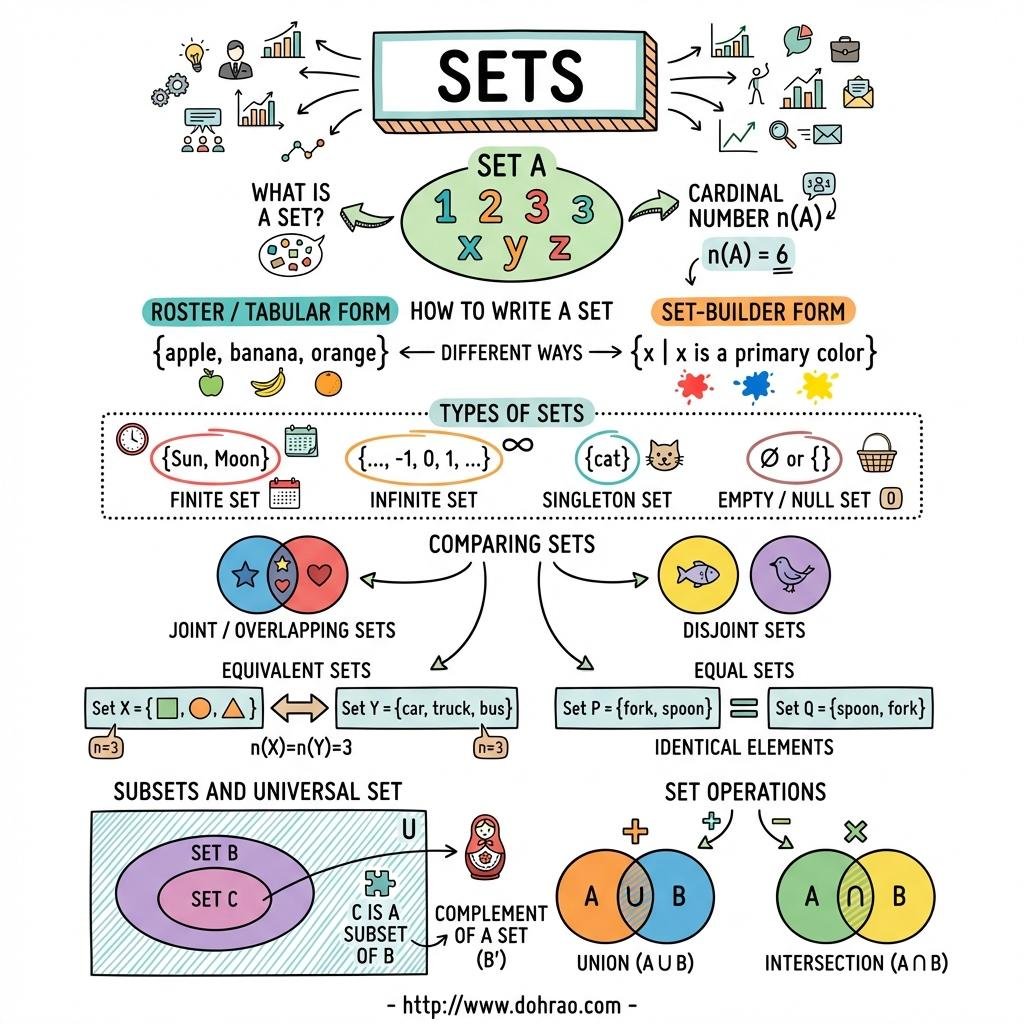
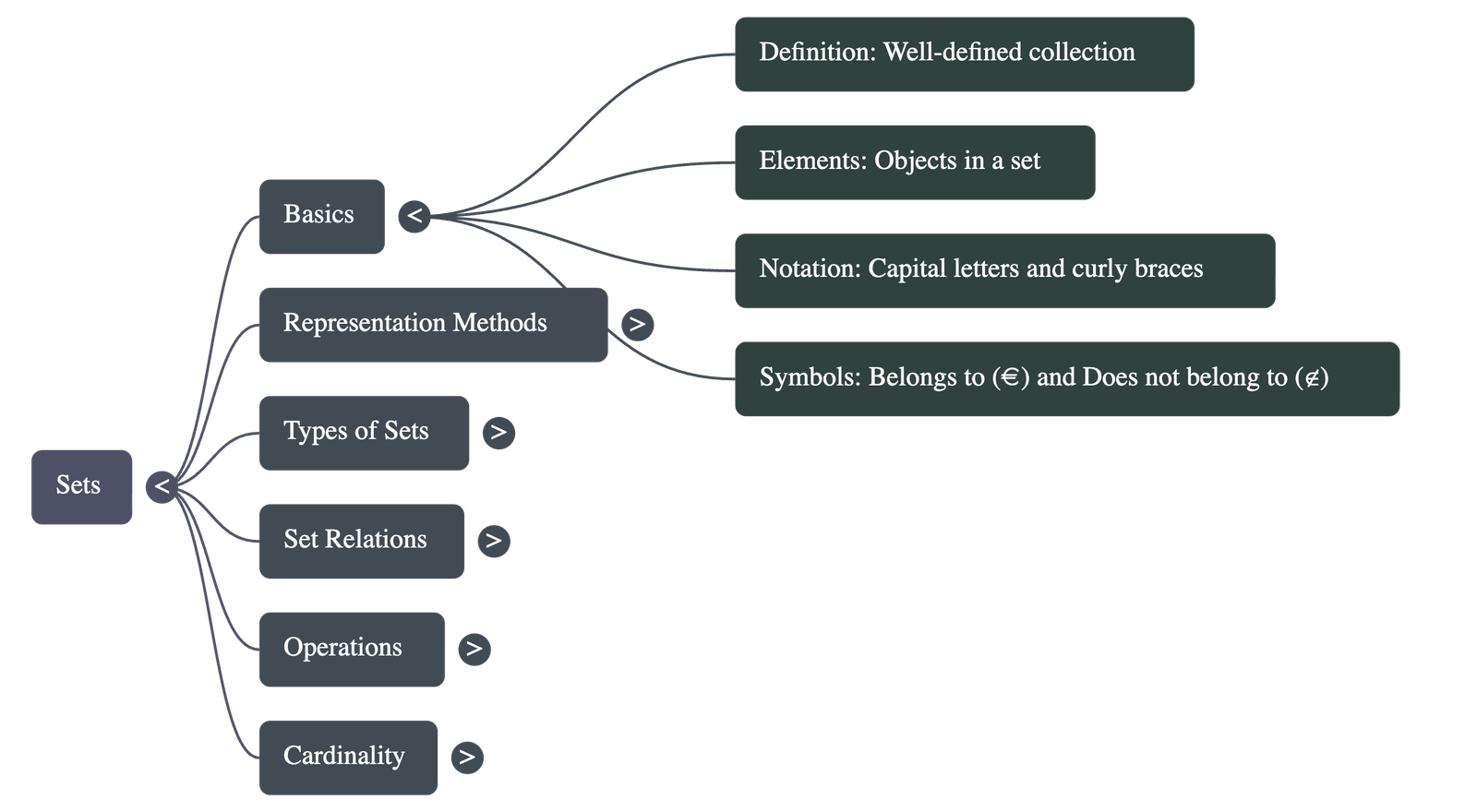
• Definition: A set is a well-defined collection of objects. "Well-defined" means there is no doubt whether a particular object belongs to the collection or not.
• Elements: The objects used to form a set are called elements or members.
• Notation: The symbol ∈ indicates "belongs to," and ∉ indicates "does not belong to." Sets are typically represented by capital letters and elements are enclosed in curly braces { }.

2. Representation of Sets

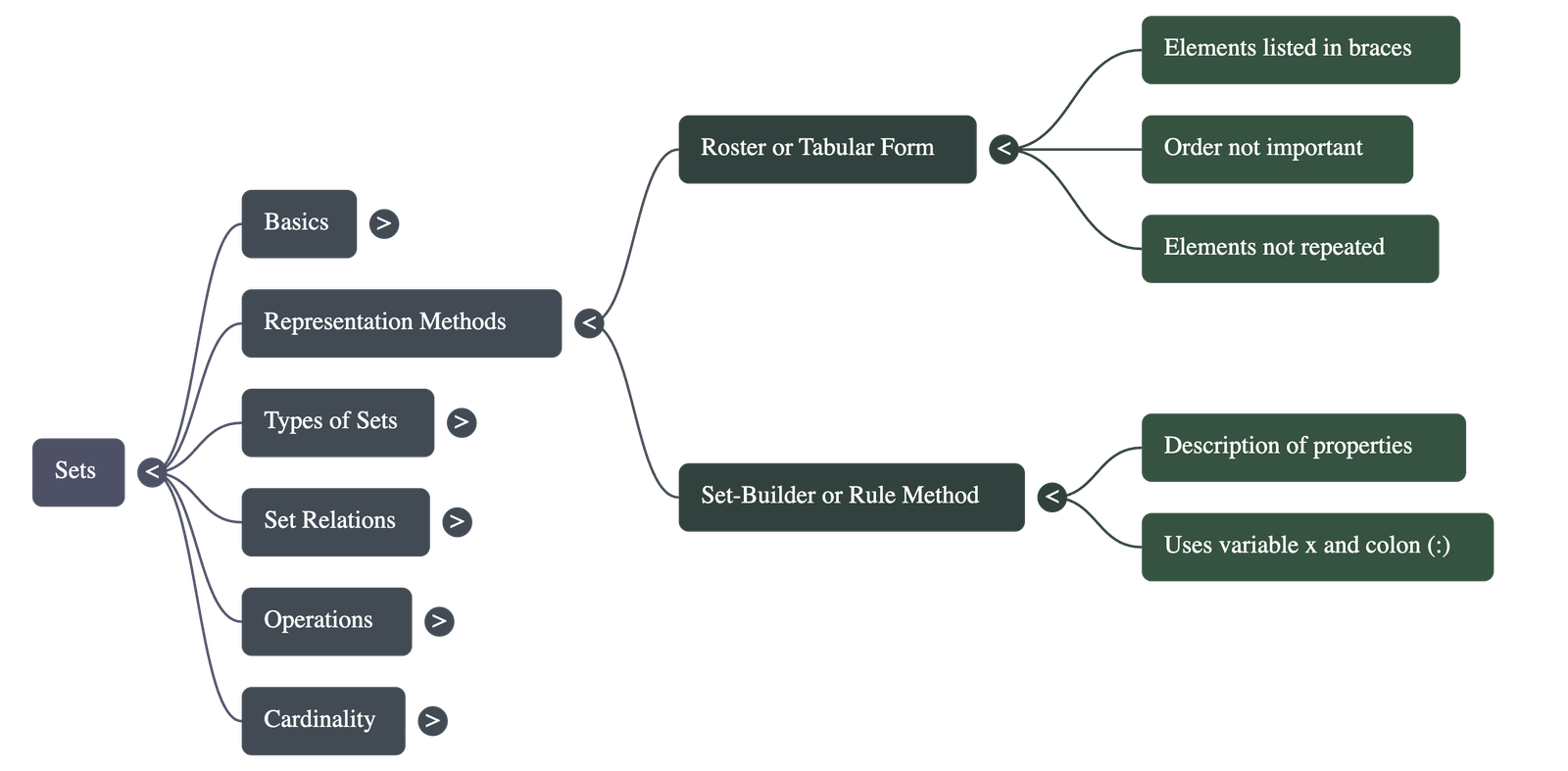
• Roster (Tabular) Form: Elements are listed individually, separated by commas, inside braces. The order of elements does not matter, and each element is written only once.
• Set-Builder (Rule) Method: Elements are described by a statement or formula expressing a common property. The symbol : or | is read as "such that."

3. Types of Sets

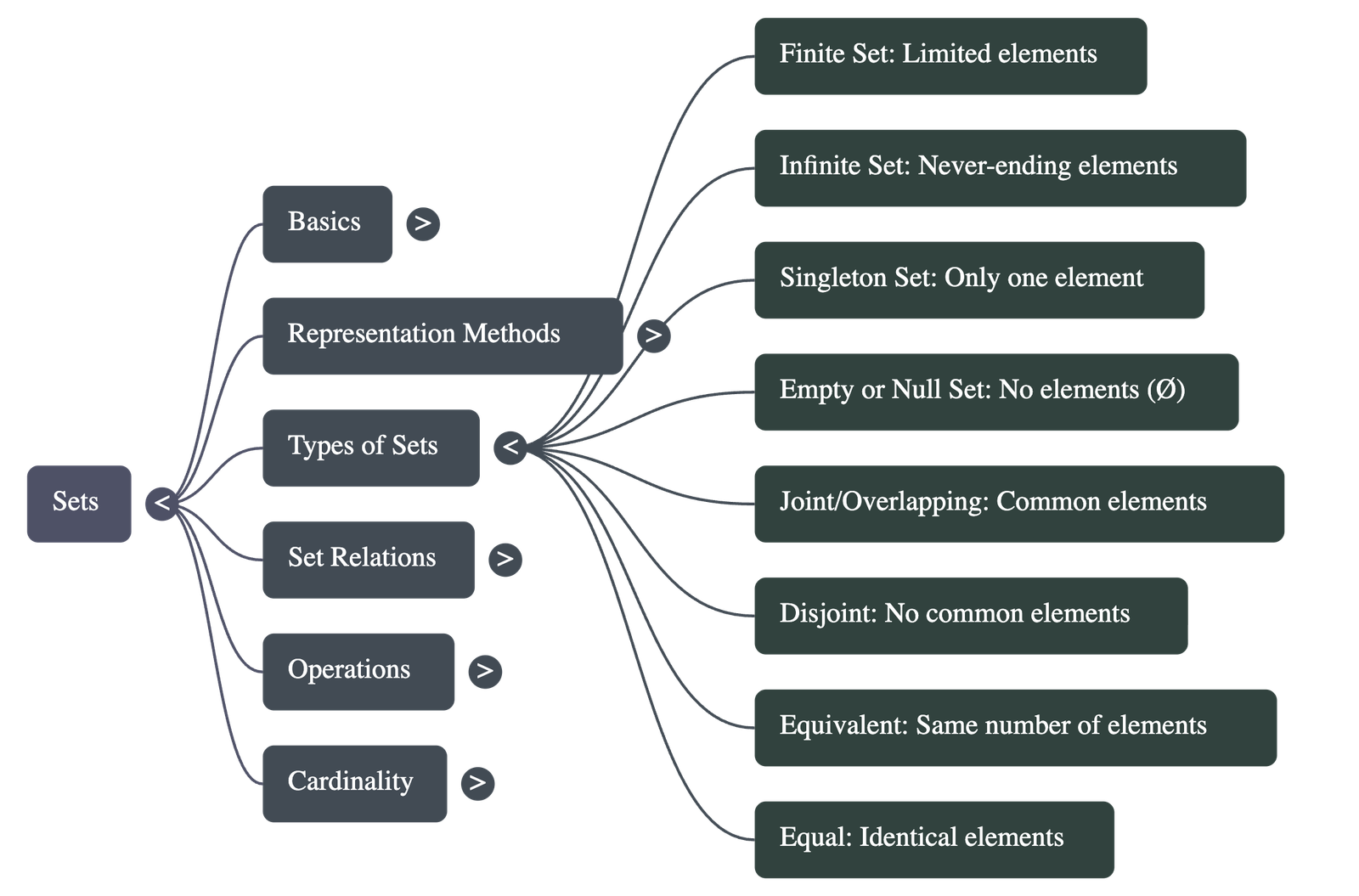
• Finite Set: A set containing a limited or countable number of elements.
• Infinite Set: A set with a never-ending number of elements.
• Singleton (Unit) Set: A set that contains exactly one element.
• Empty (Null) Set: A set containing no elements, denoted by ∅ or { }. Note: {0} is NOT an empty set.

4. Relationships Between Sets

• Joint (Overlapping) Sets: Two sets that have at least one element in common.
• Disjoint Sets: Sets that have no elements in common.
• Equivalent Sets: Sets that have the same number of elements (cardinality), even if the elements are different.
• Equal Sets: Sets that have identical elements. Equal sets are always equivalent, but equivalent sets are not necessarily equal.

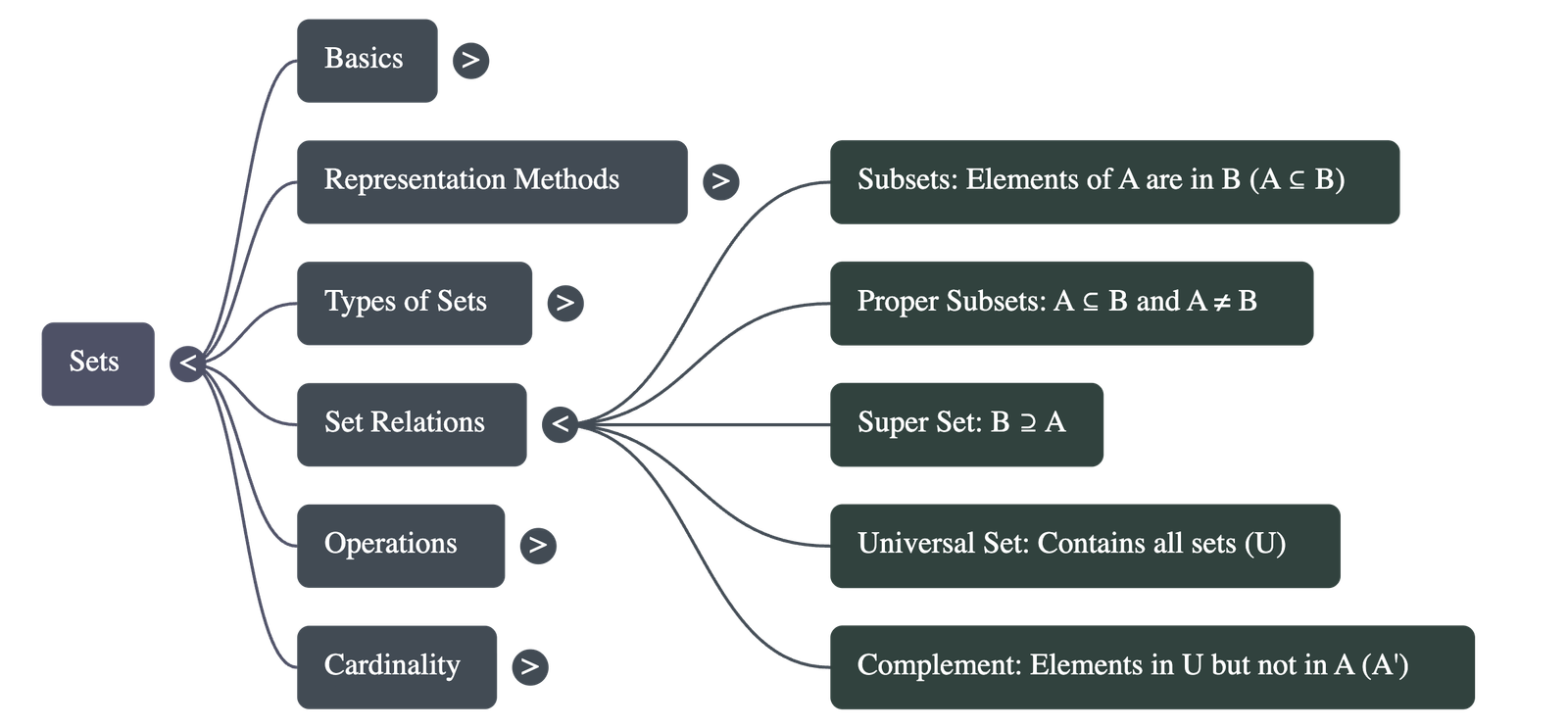
5. Subsets and Universal Sets

• Subsets: Set A is a subset of B (A ⊆ B) if every element of A is also in B. Every set is a subset of itself, and the empty set is a subset of every set.
• Proper Subsets: Set A is a proper subset of B (A ⊂ B) if all elements of A are in B, but B has at least one element not in A. No set is a proper subset of itself.
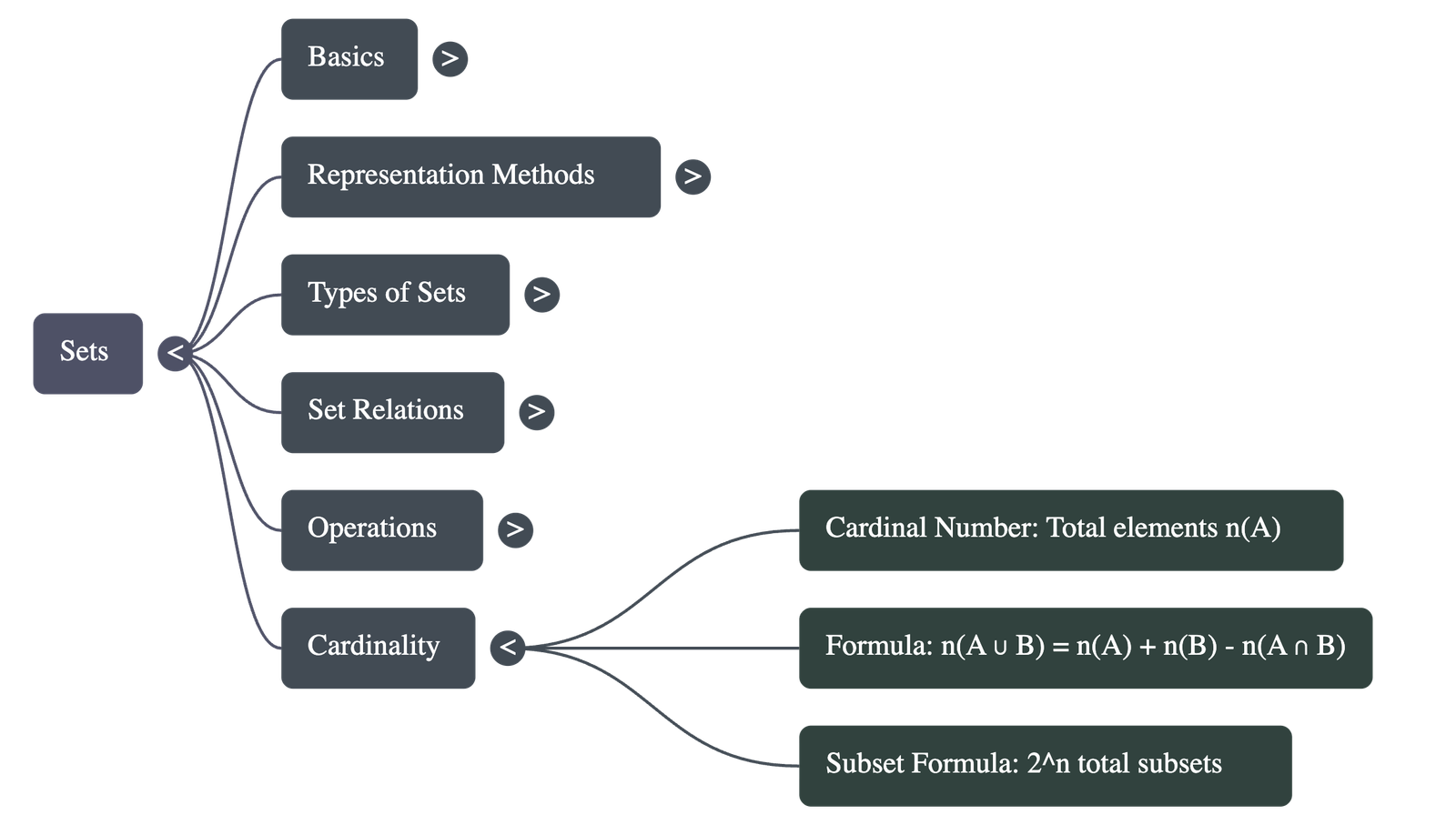
• Calculations: For a set with n elements:
  • Total number of subsets = 2ⁿ
  • Total number of proper subsets = 2ⁿ - 1
• Universal Set: A set (denoted by ξ or U) that contains all sets under consideration as its subsets.

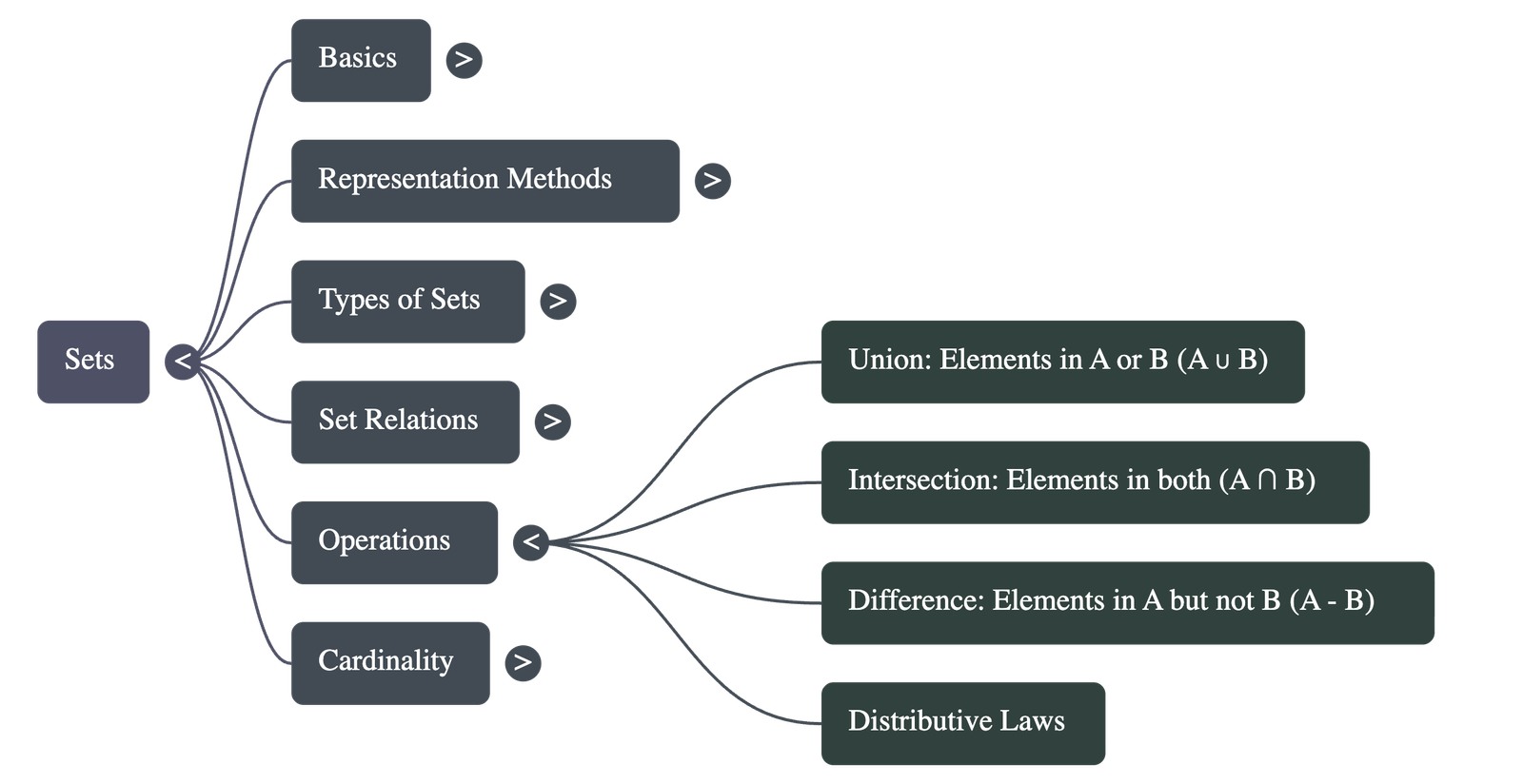
6. Set Operations

• Complement (A'): The set of all elements in the universal set that are not in set A. A set and its complement are always disjoint.
• Union (A ∪ B): A set containing all elements that belong to A, or B, or both. Union is commutative and associative.
• Intersection (A ∩ B): A set containing only the elements common to both A and B. Intersection is also commutative and associative.
• Difference (A - B): The set of elements that belong to A but not to B.

7. Distributive Laws and Cardinality

• Distributive Laws:
  • Union is distributive over intersection: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
  • Intersection is distributive over union: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
• Cardinal Number n(A): The number of distinct elements in a finite set.
• Fundamental Formula: For any two finite sets A and B:
  n(A ∪ B) = n(A) + n(B) - n(A ∩ B)