Rational Numbers - Summary

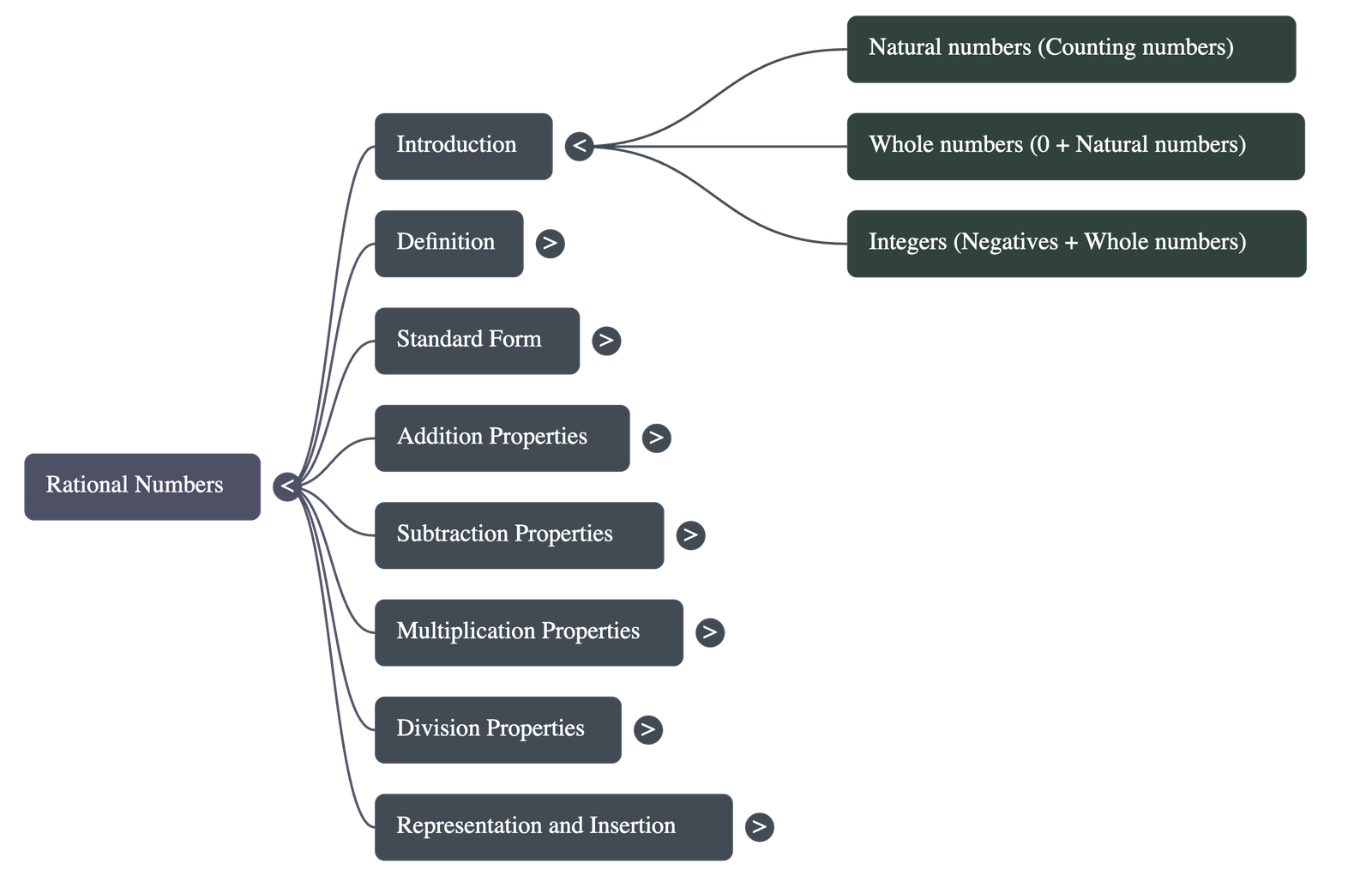
1. Basic Number Categories and Definitions
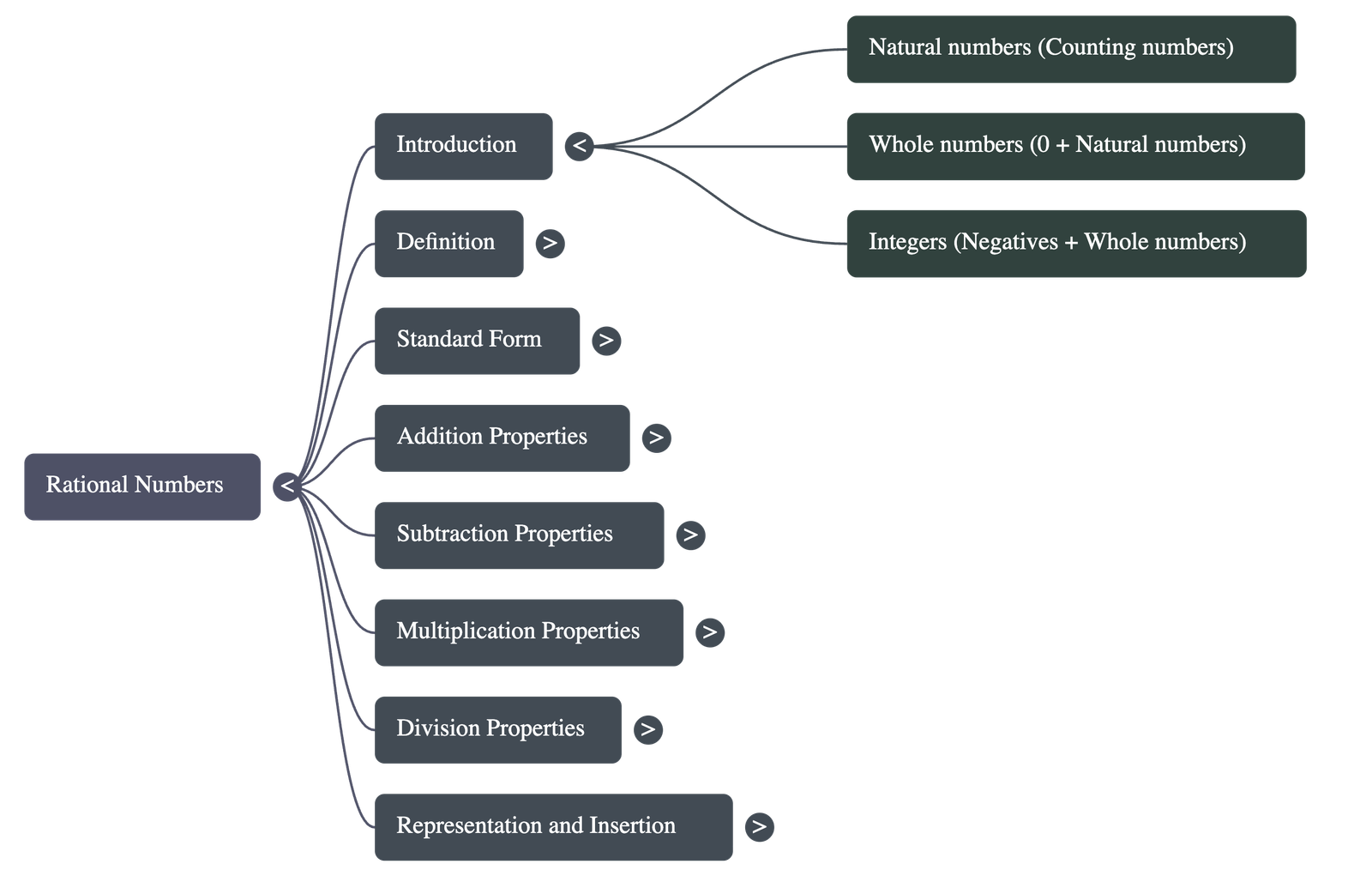
   • Natural Numbers: These are counting numbers like 1, 2, 3, 4, 5....
   • Whole Numbers: Includes 0 (zero) along with all natural numbers.
   • Integers: Consist of negative natural numbers combined with whole numbers.
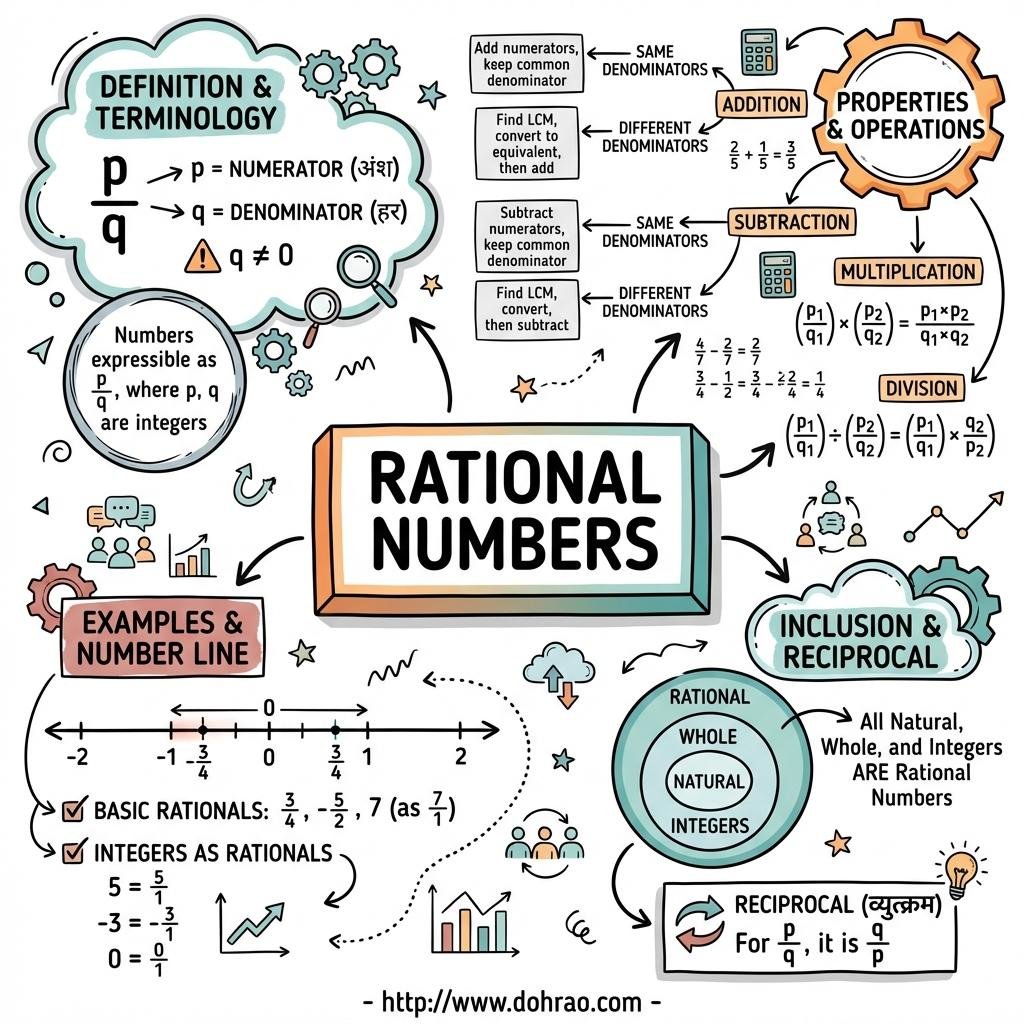
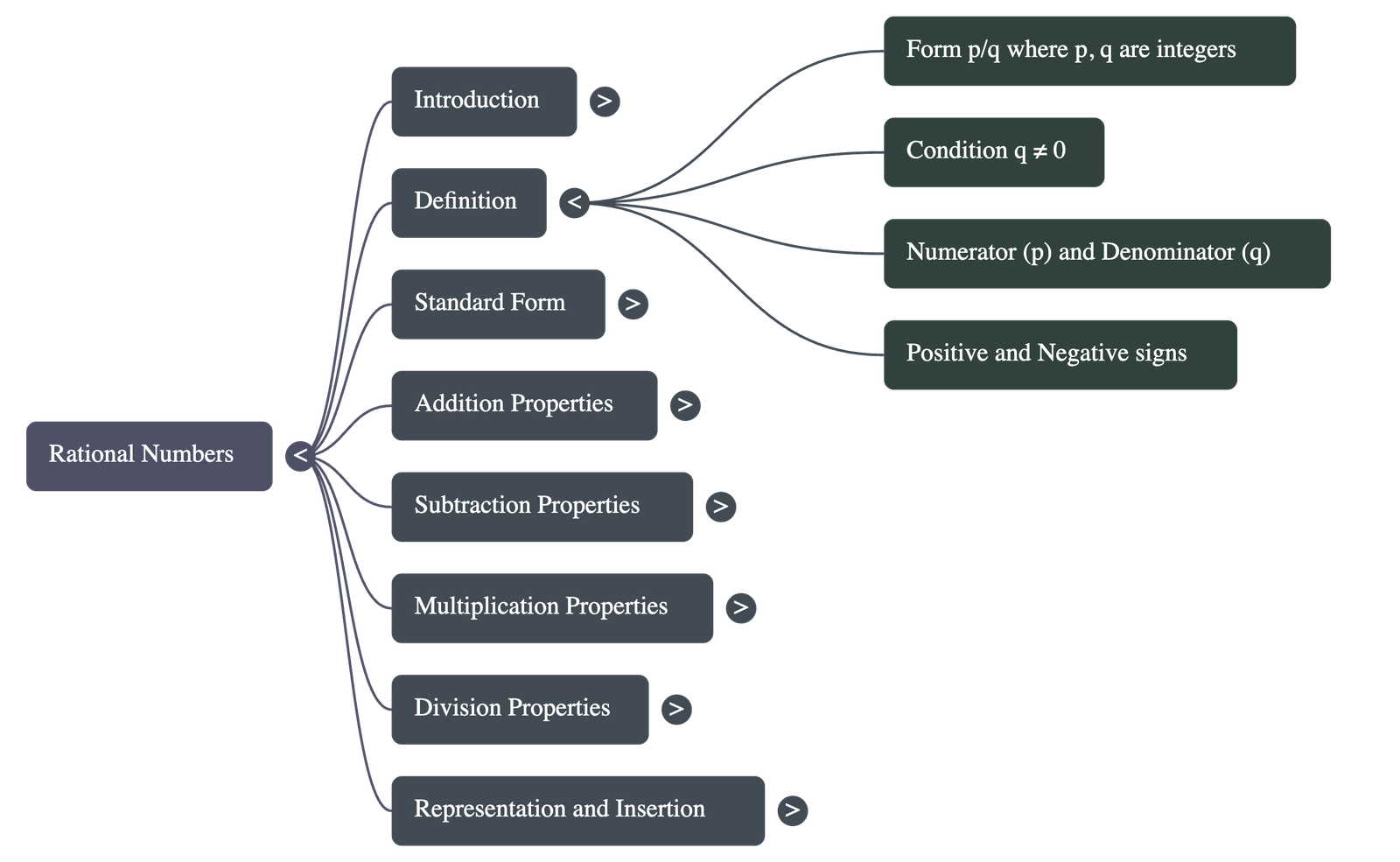
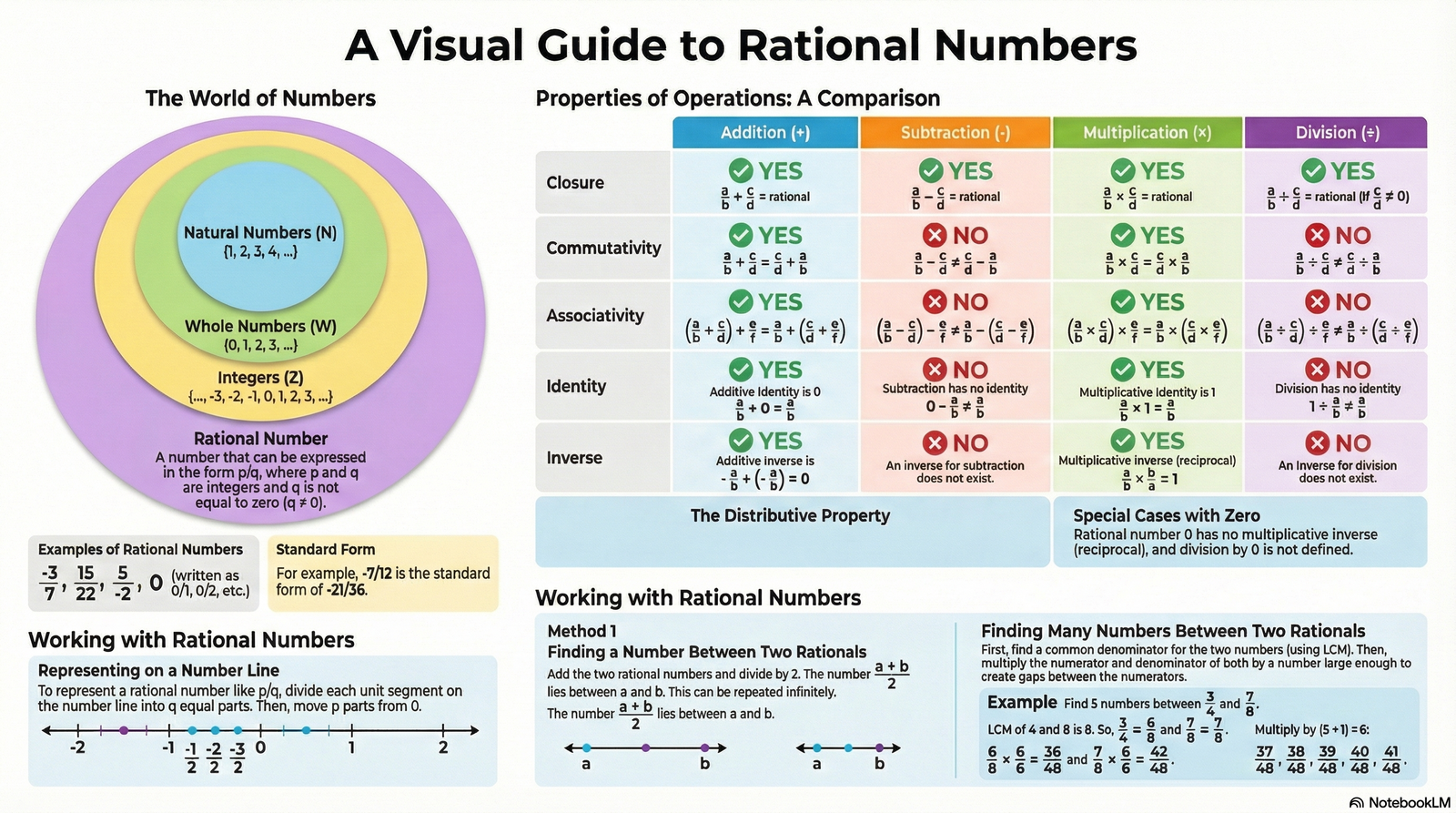
   • Rational Numbers: Any number that can be expressed in the form q p ​ , where p and q are integers and q  =0.
   • Inclusions: Every natural number, whole number, integer, and fraction is a rational number; zero (0) is also a rational number because it can be written as 1 0 ​ , 5 0 ​ , etc.
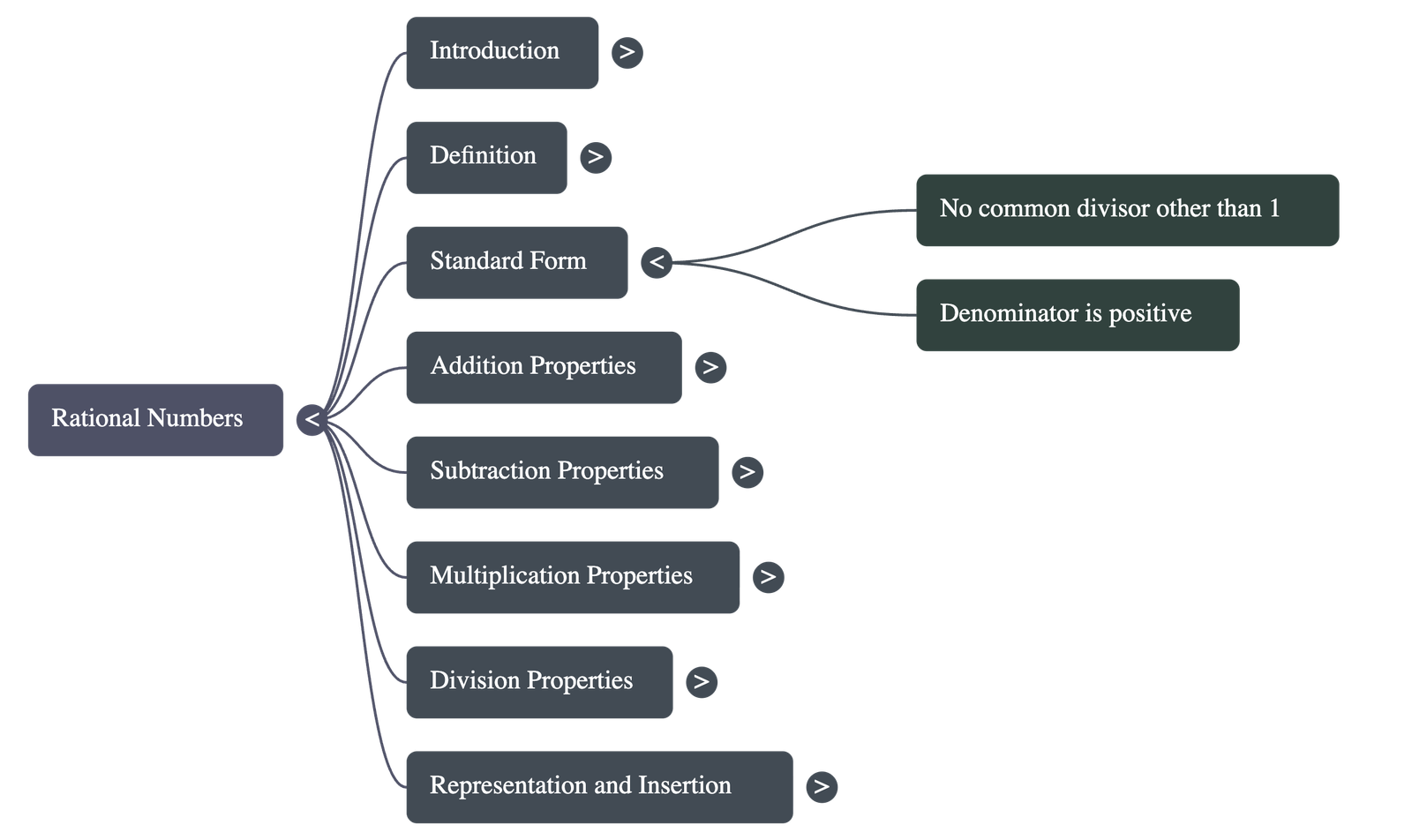
   • Standard Form: A rational number is in standard form if p and q have no common divisor other than 1 and the denominator q is positive.
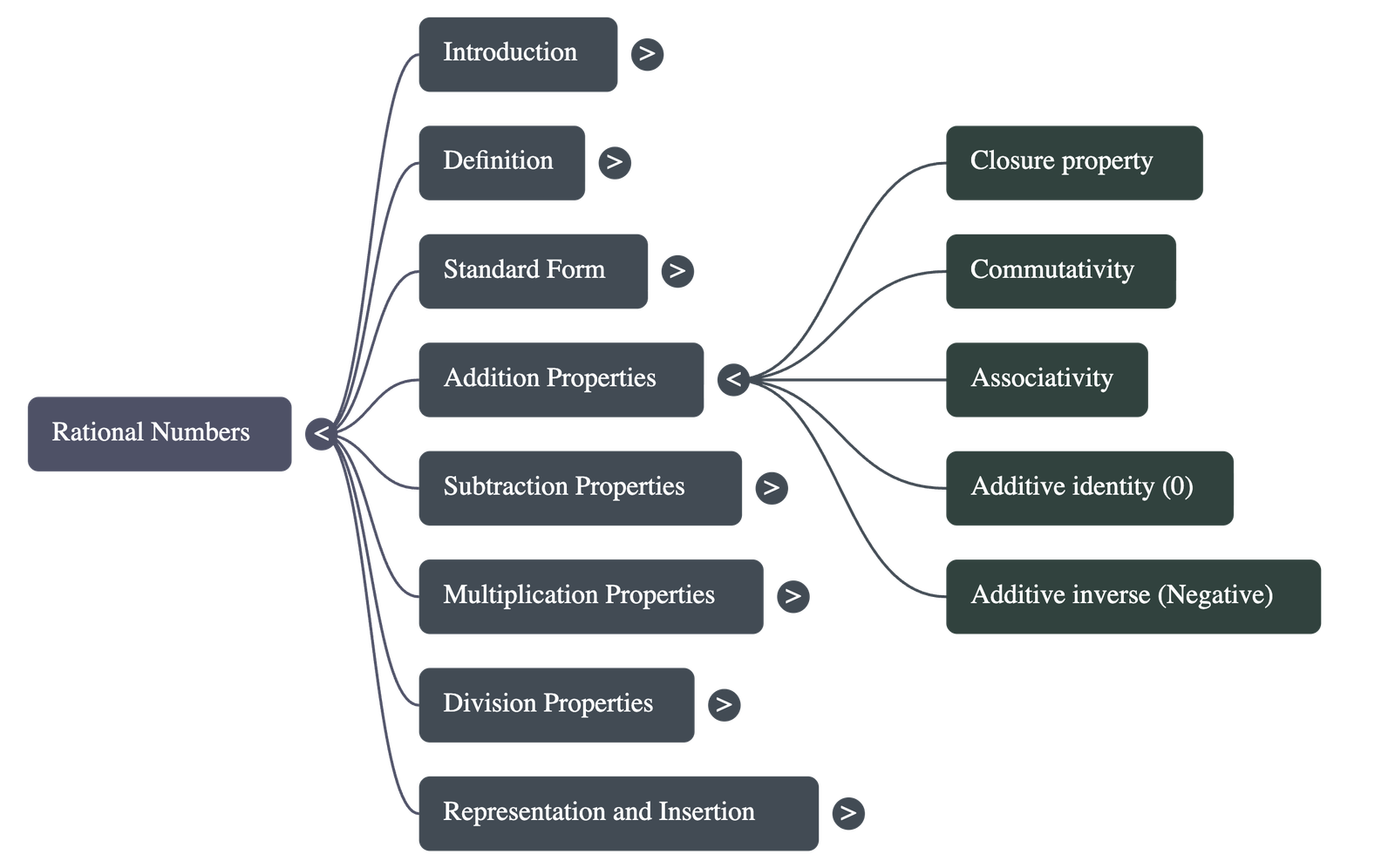
2. Properties of Addition
   • Closure: The sum of two rational numbers is always a rational number.
   • Commutativity: The order of addition does not matter: b a ​ + d c ​ = d c ​ + b a ​ .
   • Associativity: The grouping of numbers does not change the sum.
   • Additive Identity: Zero (0) is the identity element; adding it to any rational number leaves the number unchanged.
   • Additive Inverse: Every rational number b a ​ has an inverse − b a ​ such that their sum is zero.
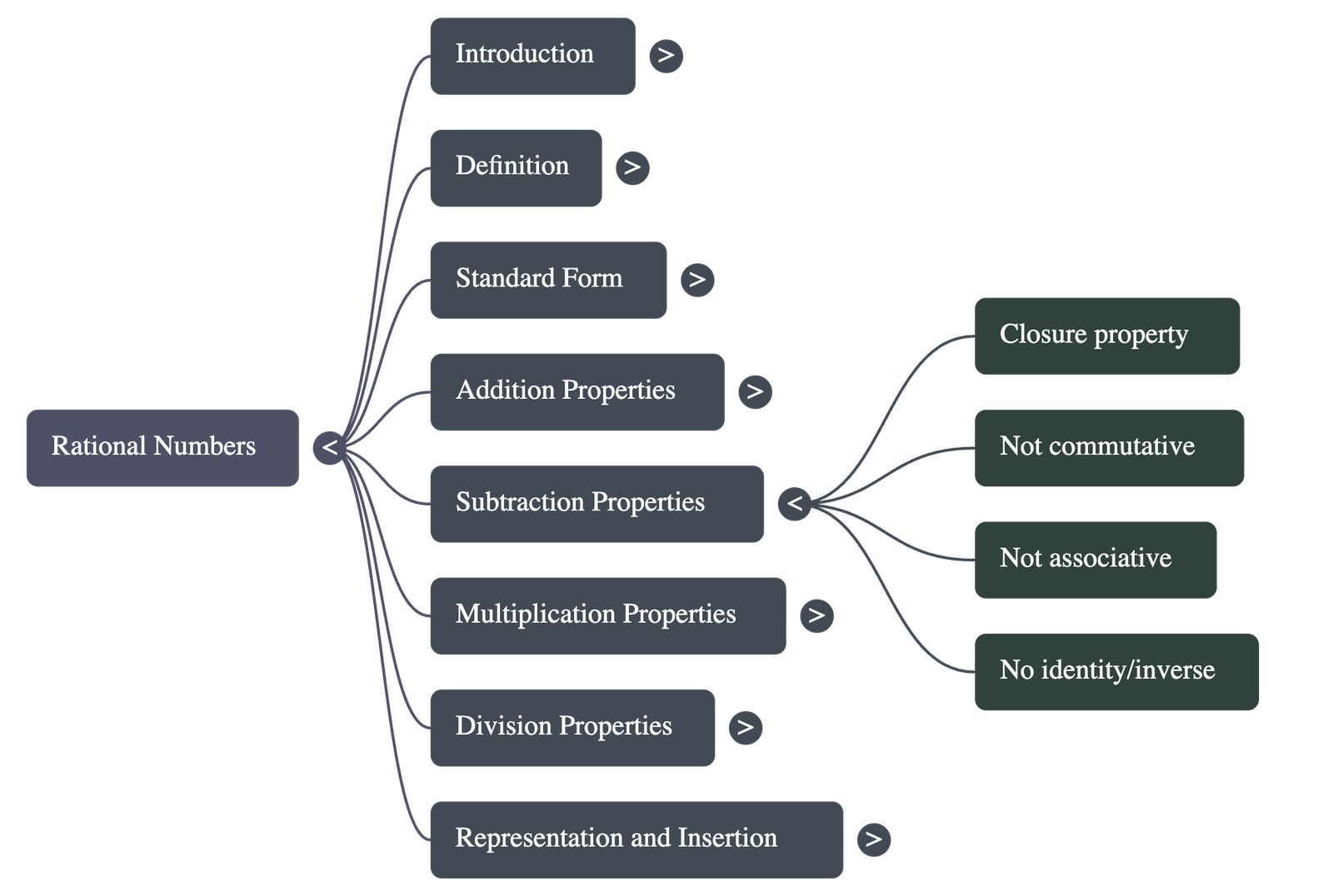
3. Properties of Subtraction
   • Closure: Subtraction of two rational numbers results in a rational number.
   • Non-Commutative and Non-Associative: Unlike addition, the order and grouping of numbers do matter in subtraction.
   • Identity/Inverse: Subtraction has no general identity element and no existence of inverse.
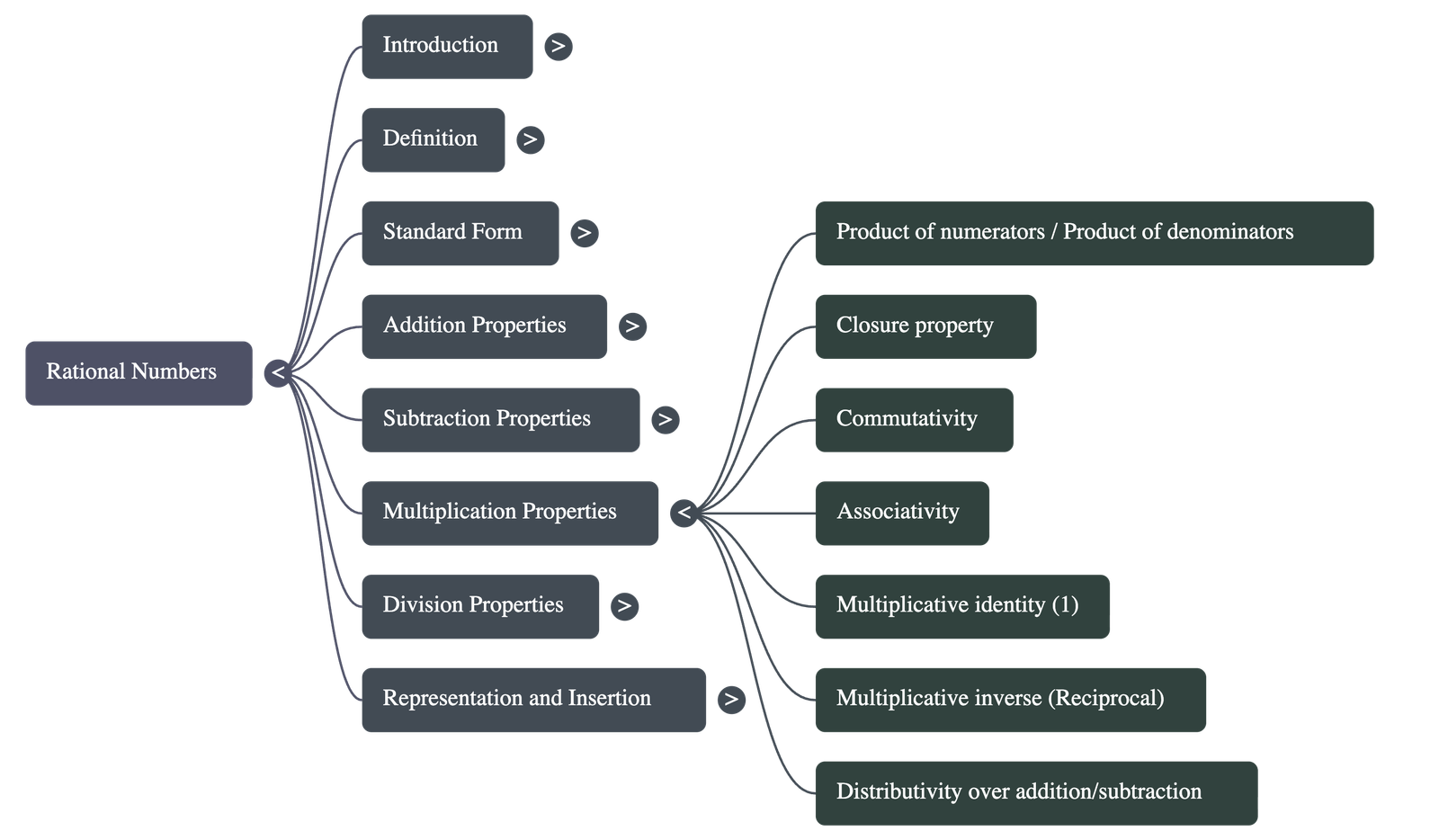
4. Properties of Multiplication
   • Calculation: The product is found by multiplying the numerators together and the denominators together.
   • Closure: The product of two rational numbers is always a rational number.
   • Commutativity and Associativity: Multiplication follows both properties, meaning order and grouping do not affect the result.
   • Multiplicative Identity: One (1) is the multiplicative identity.
   • Multiplicative Inverse (Reciprocal): For a non-zero rational number b a ​ , the reciprocal is a b ​ . Their product is 1.
     • Note: Zero (0) has no multiplicative inverse.
   • Distributivity: Multiplication is distributive over both addition and subtraction.
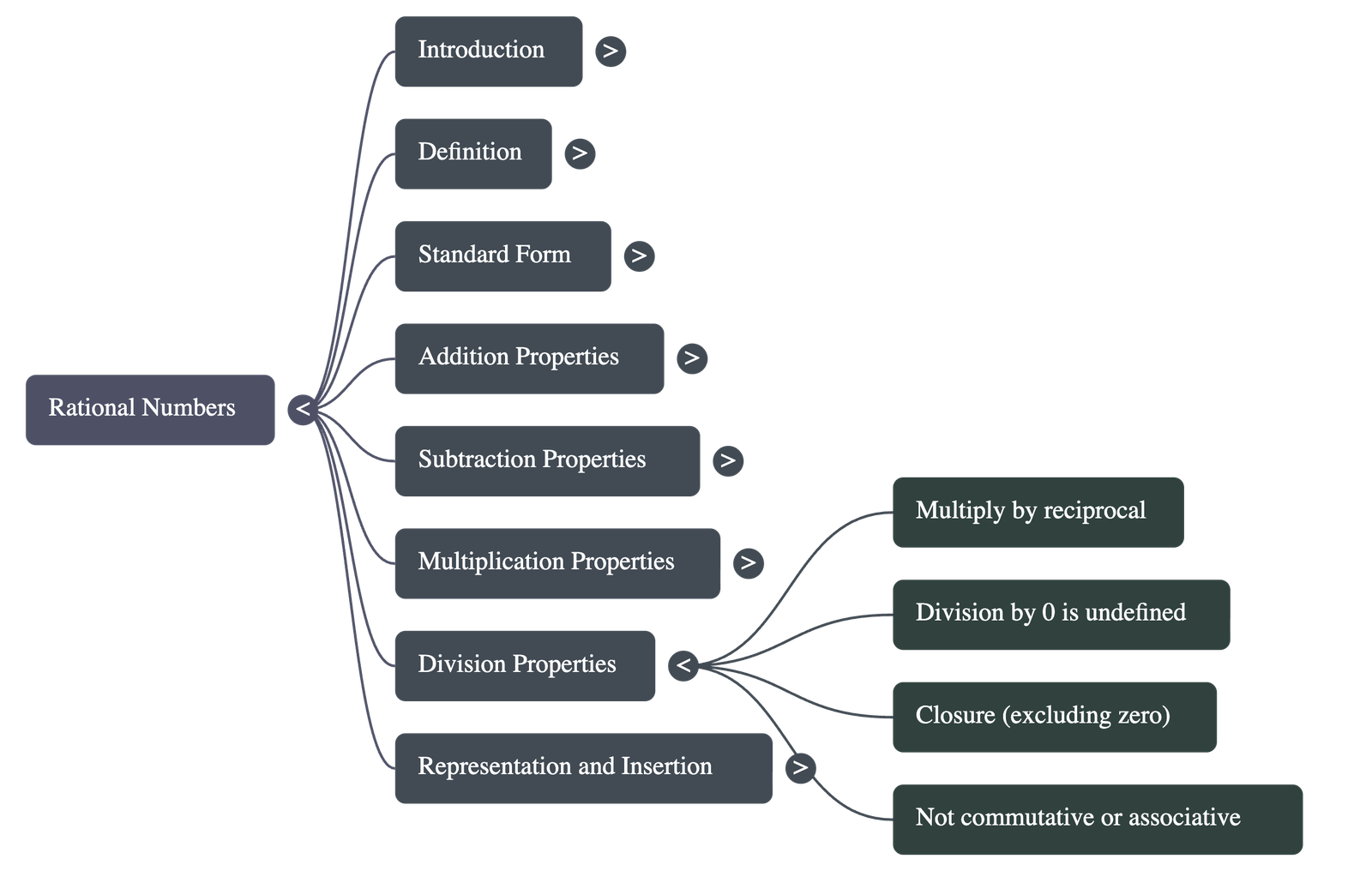
5. Properties of Division
   • Calculation: Dividing by a rational number is equivalent to multiplying by its reciprocal.
   • Division by Zero: Division by zero is not defined.
   • Non-Commutative and Non-Associative: Division does not follow these properties.
   • Closure: Division is closed for all rational numbers except when dividing by zero.
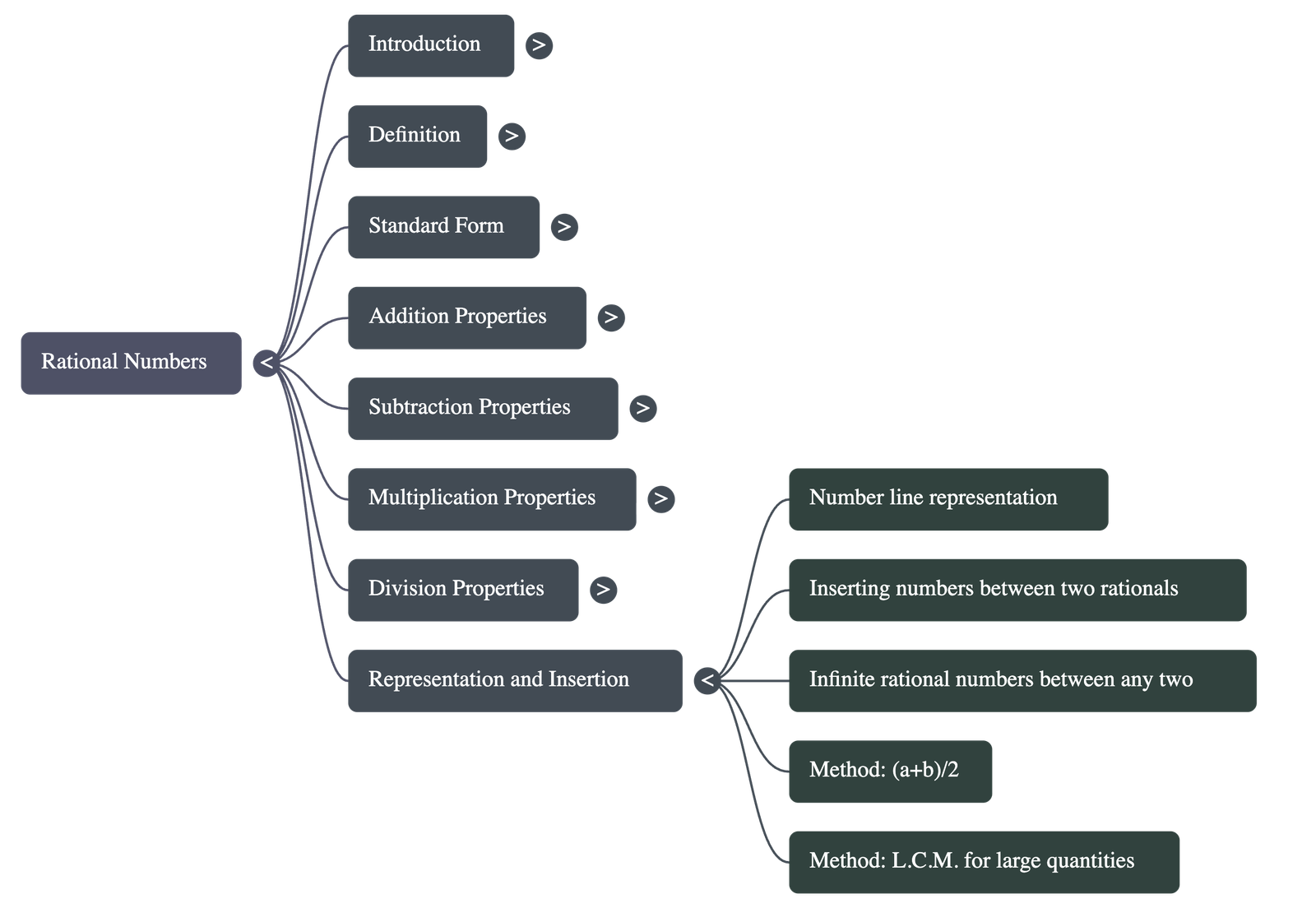
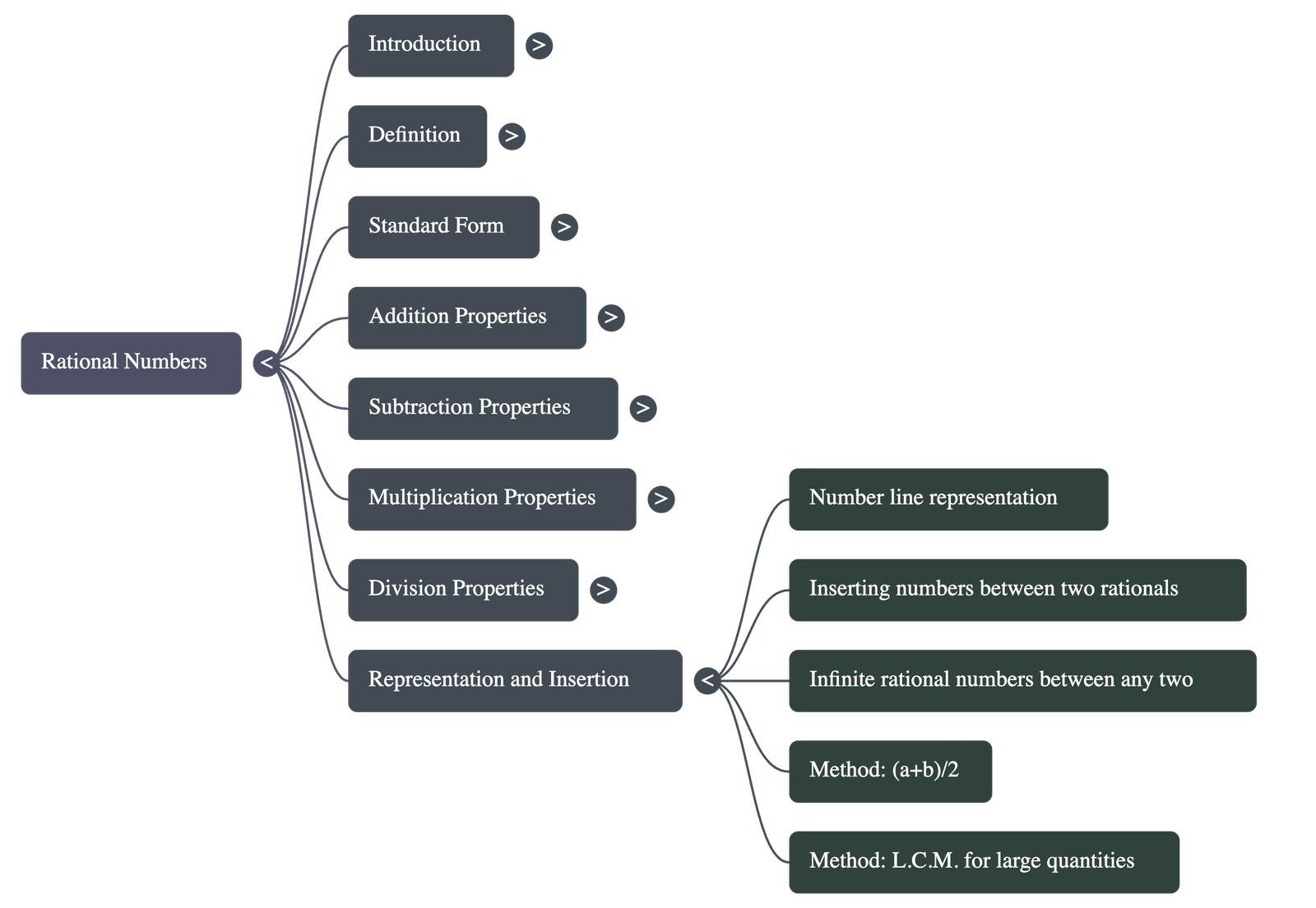
6. Representation and Insertion
   • Number Line: Rational numbers can be represented on a number line by dividing the distance between integers into equal parts based on the denominator.
   • Density: There are infinitely many rational numbers between any two given rational numbers.
   • Finding Numbers Between:
     • One method is using the average: 2 a+b ​ .
     • Another method for finding many numbers involves making the denominators equal (using LCM) and then increasing the numerator and denominator to create a larger range.