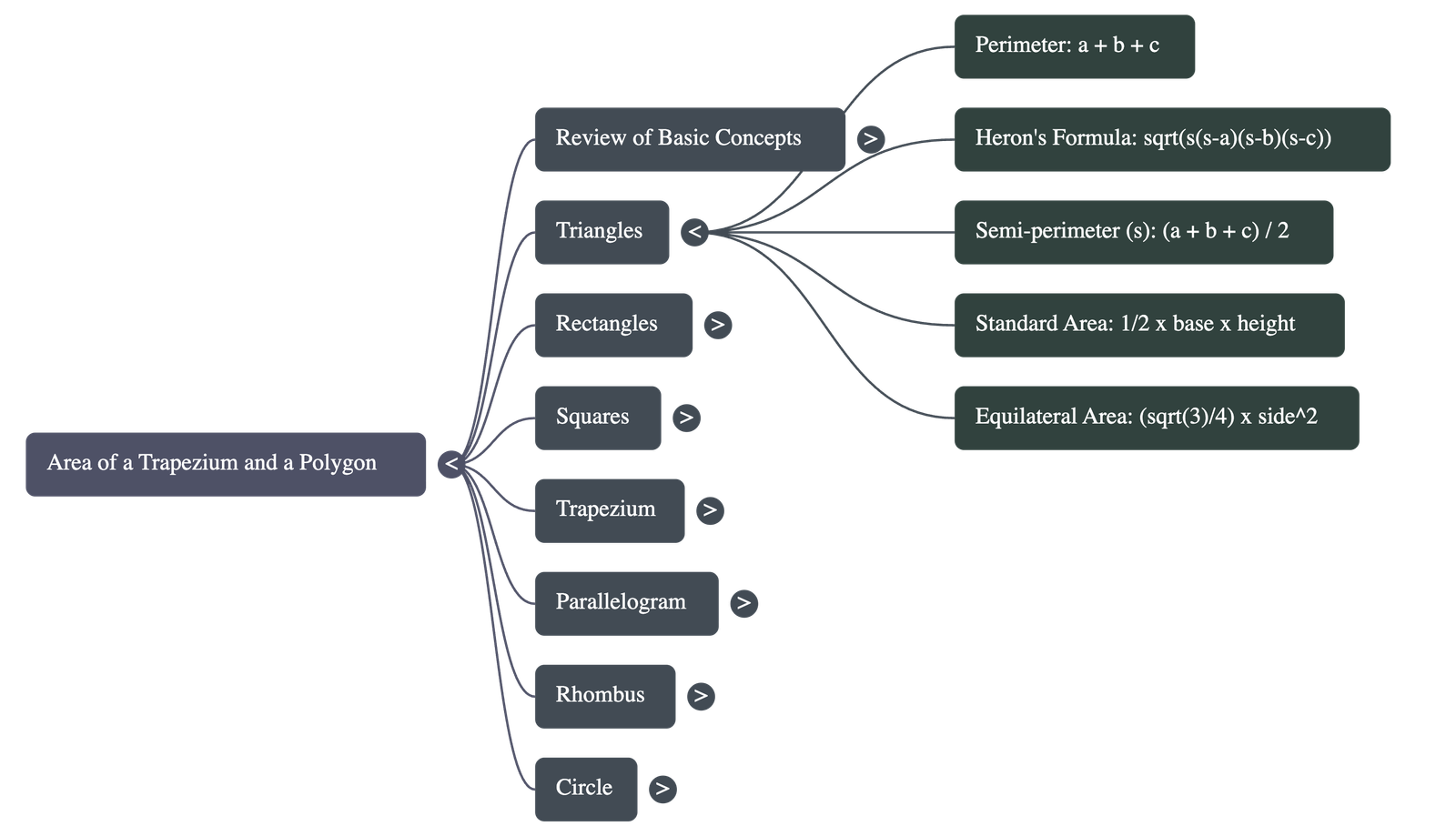
Chapter 22: Area of a Trapezium and a Polygon

1. Fundamentals of Mensuration

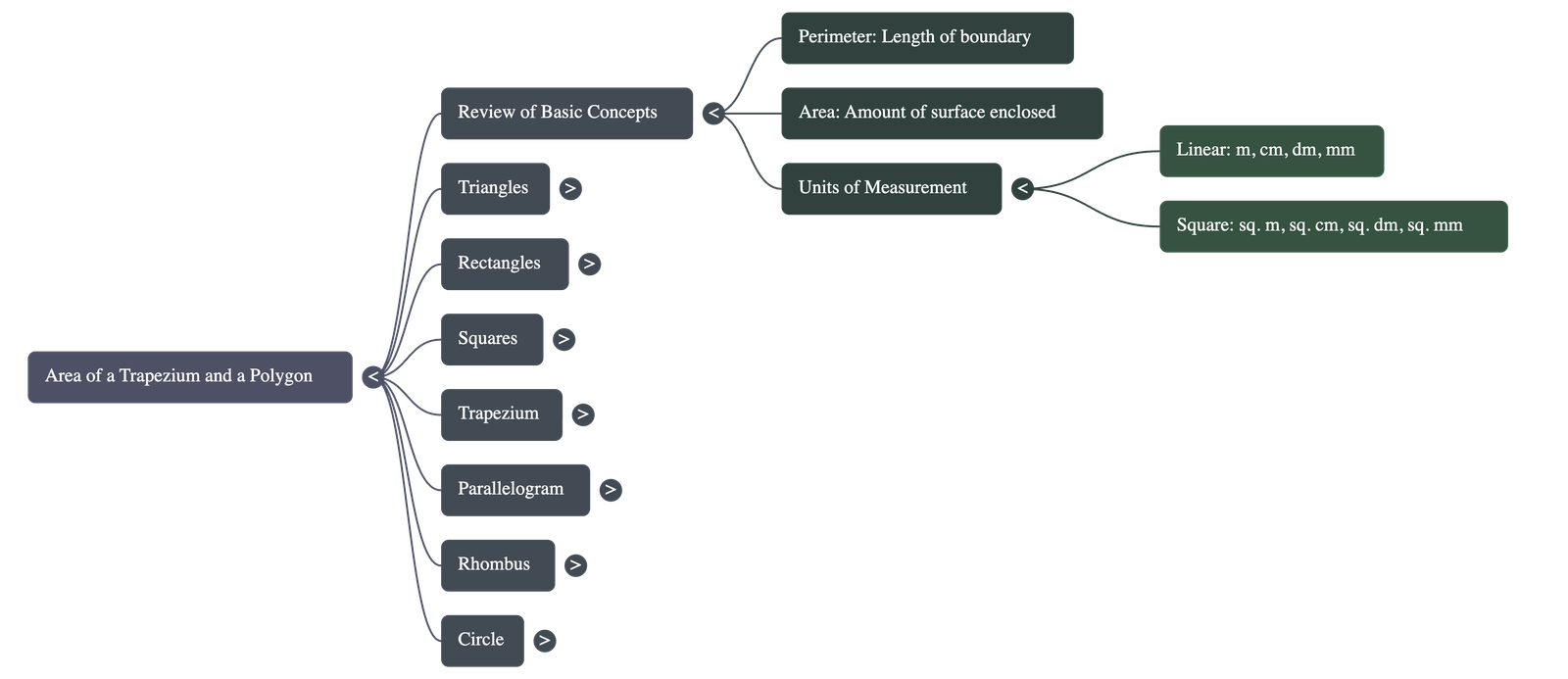
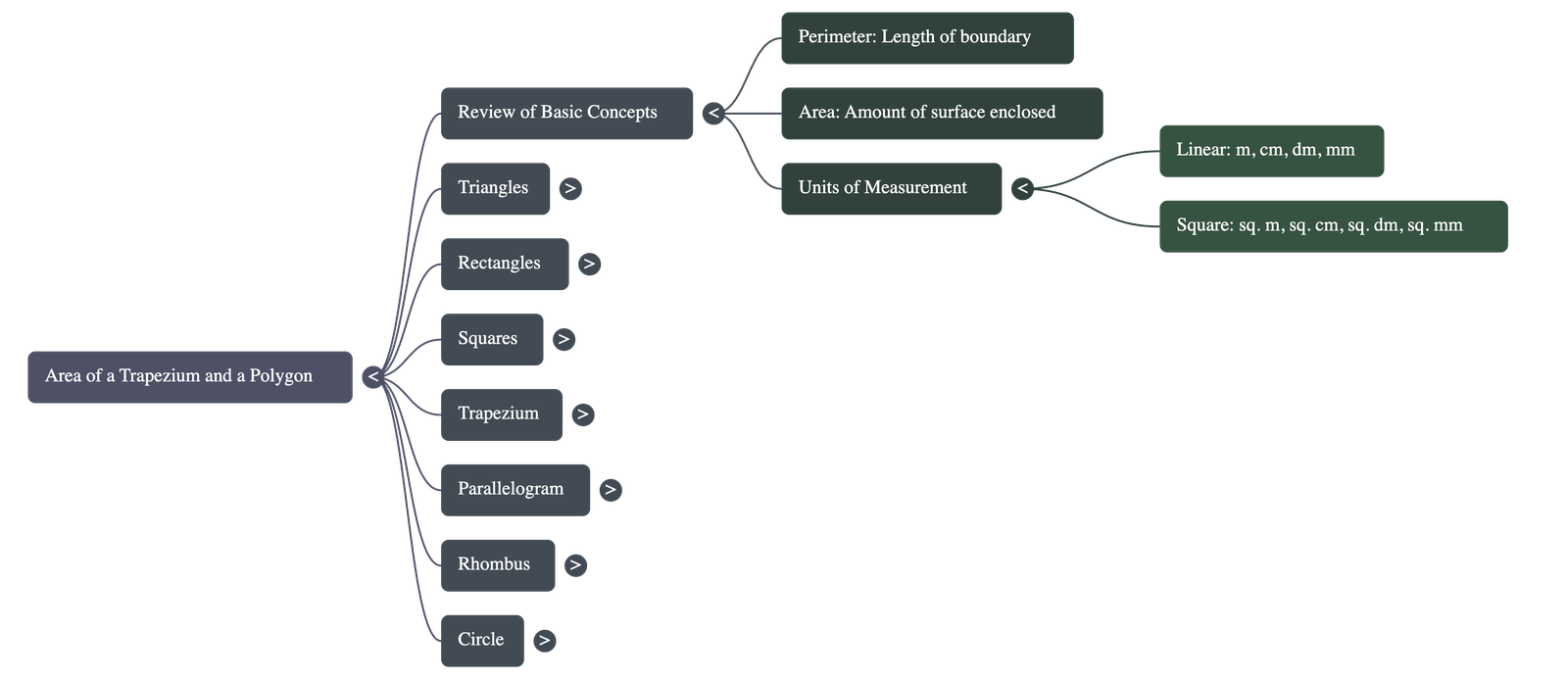
• Perimeter is defined as the total length of the boundary of a plane figure.
• Area represents the total amount of surface enclosed by the boundaries of a figure.
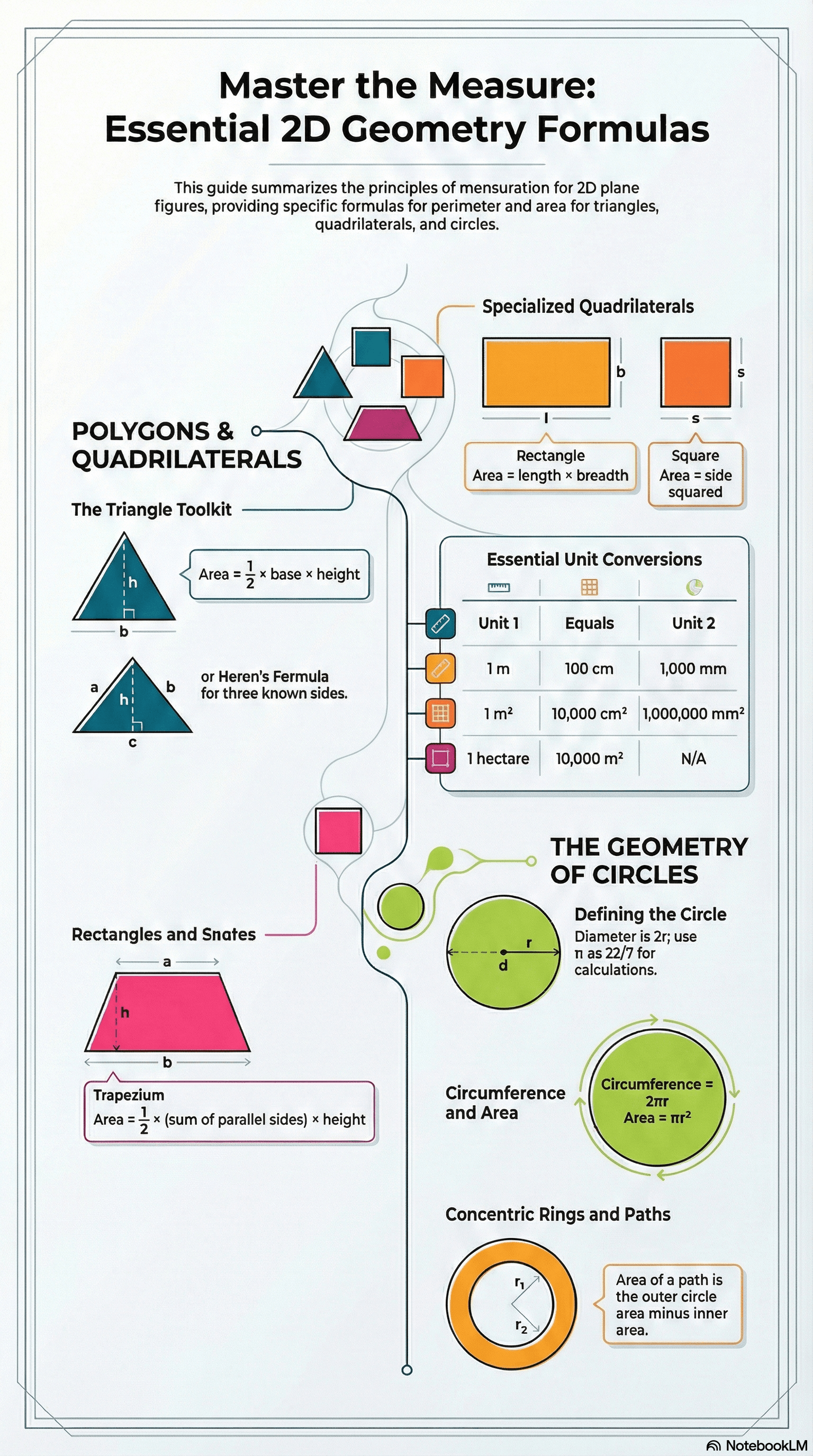
• Standard units for length include metres (m), centimetres (cm), millimetres (mm), and decimetres (dm).
• Area is measured in square units, such as square metres (m²) or square centimetres (cm²).

2. Perimeter and Area of Triangles

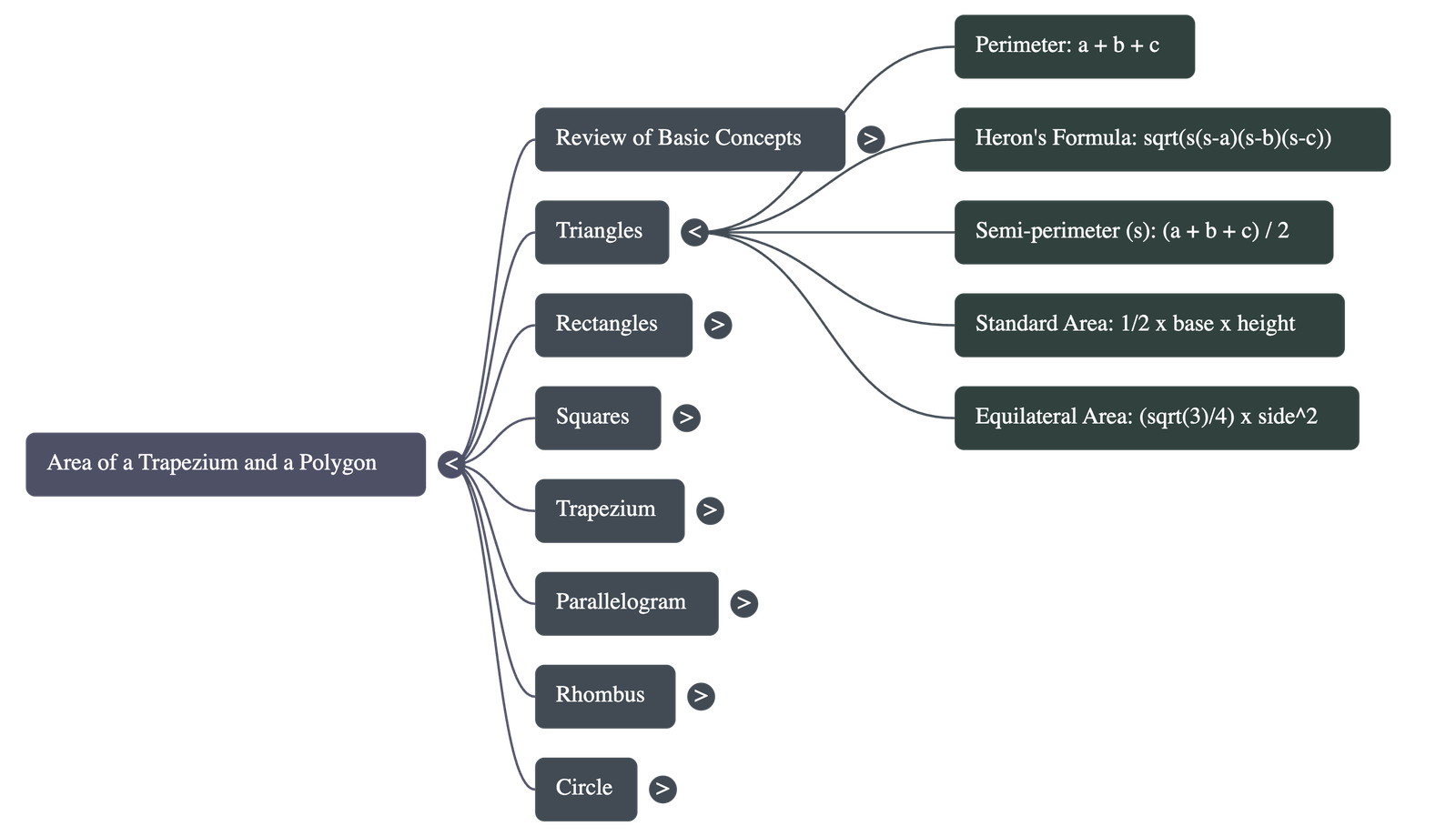
• For a triangle with sides a, b, and c, the perimeter is a + b + c.
• Heron’s Formula: Used when all three sides are known.
  Area = √[s(s - a)(s - b)(s - c)], where s (semi-perimeter) = (a + b + c) / 2.
• Base-Height Formula: Used when the base and corresponding altitude (height) are known.
  Area = 1/2 × base × height
• Equilateral Triangles: For a triangle where all sides are a:
  Area = (√3 / 4) × a²

3. Rectangles and Squares

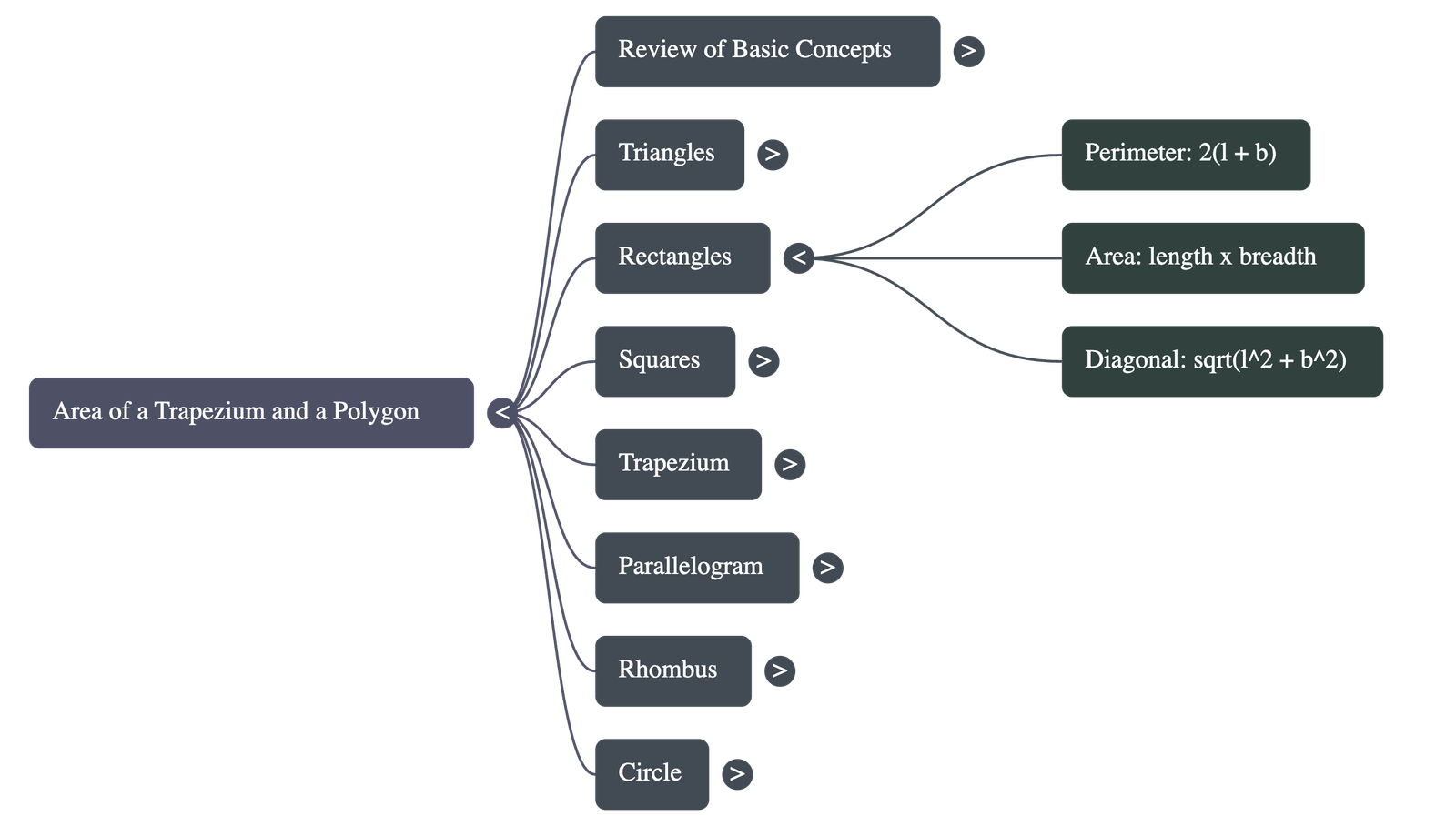
• Rectangle:
  Perimeter = 2(length + breadth)
  Area = length × breadth
  Diagonal = √(length² + breadth²)
• Square:
  Perimeter = 4 × side
  Area = (side)² or 1/2 × (diagonal)²
  Diagonal = side × √2

4. Special Quadrilaterals

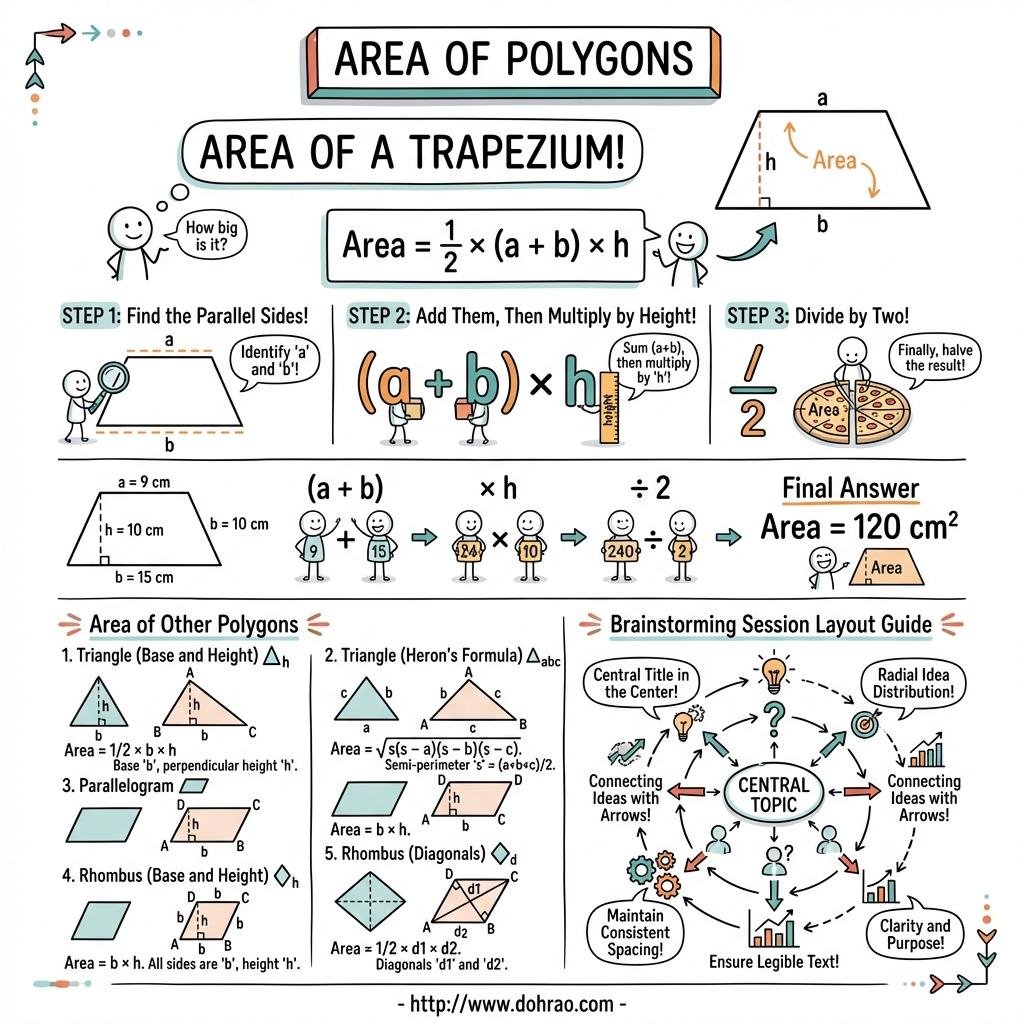
• Trapezium: A figure with one pair of parallel sides.
  Area = 1/2 × (sum of parallel sides) × height
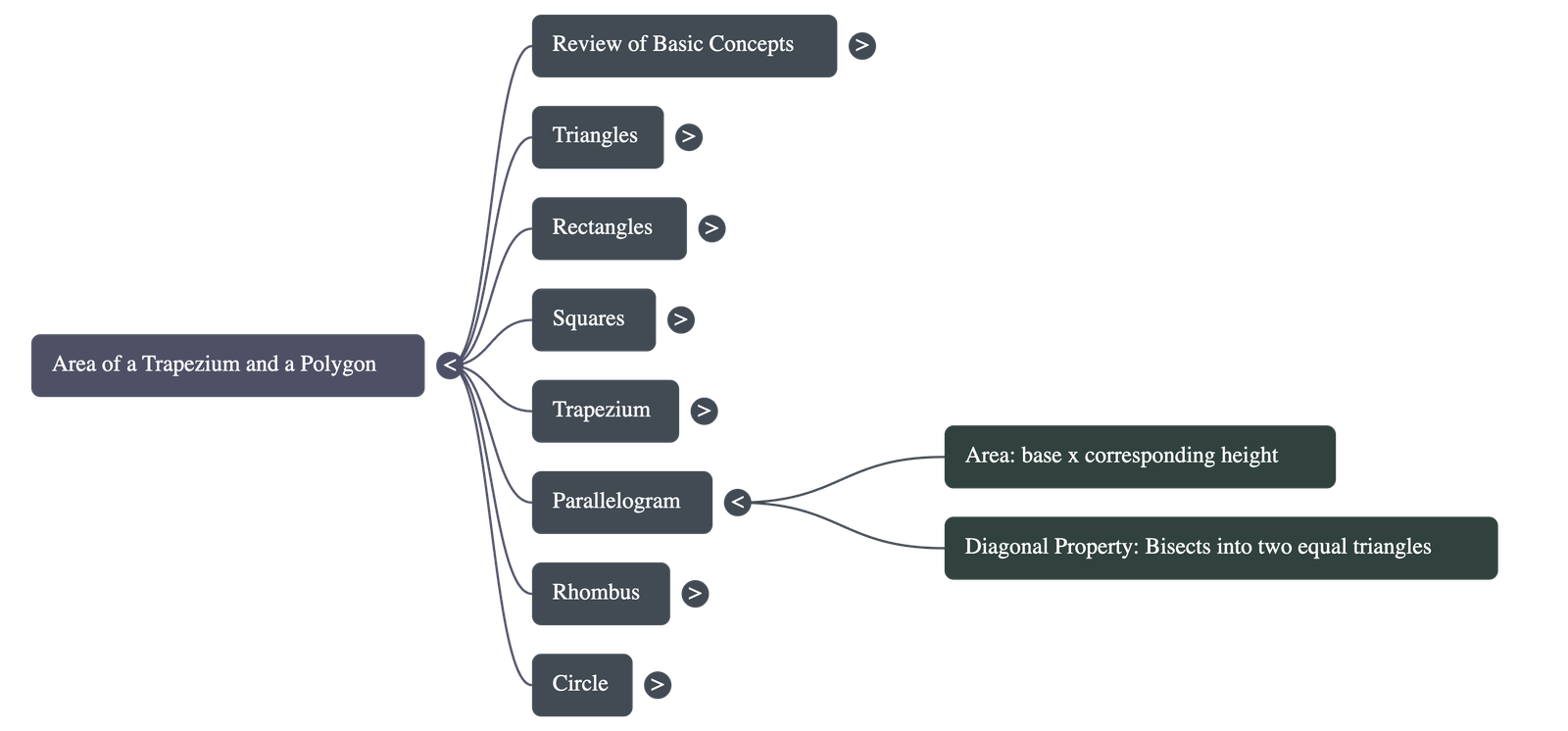
• Parallelogram:
  Area = base × corresponding height
  Note: A diagonal divides a parallelogram into two triangles of equal area.
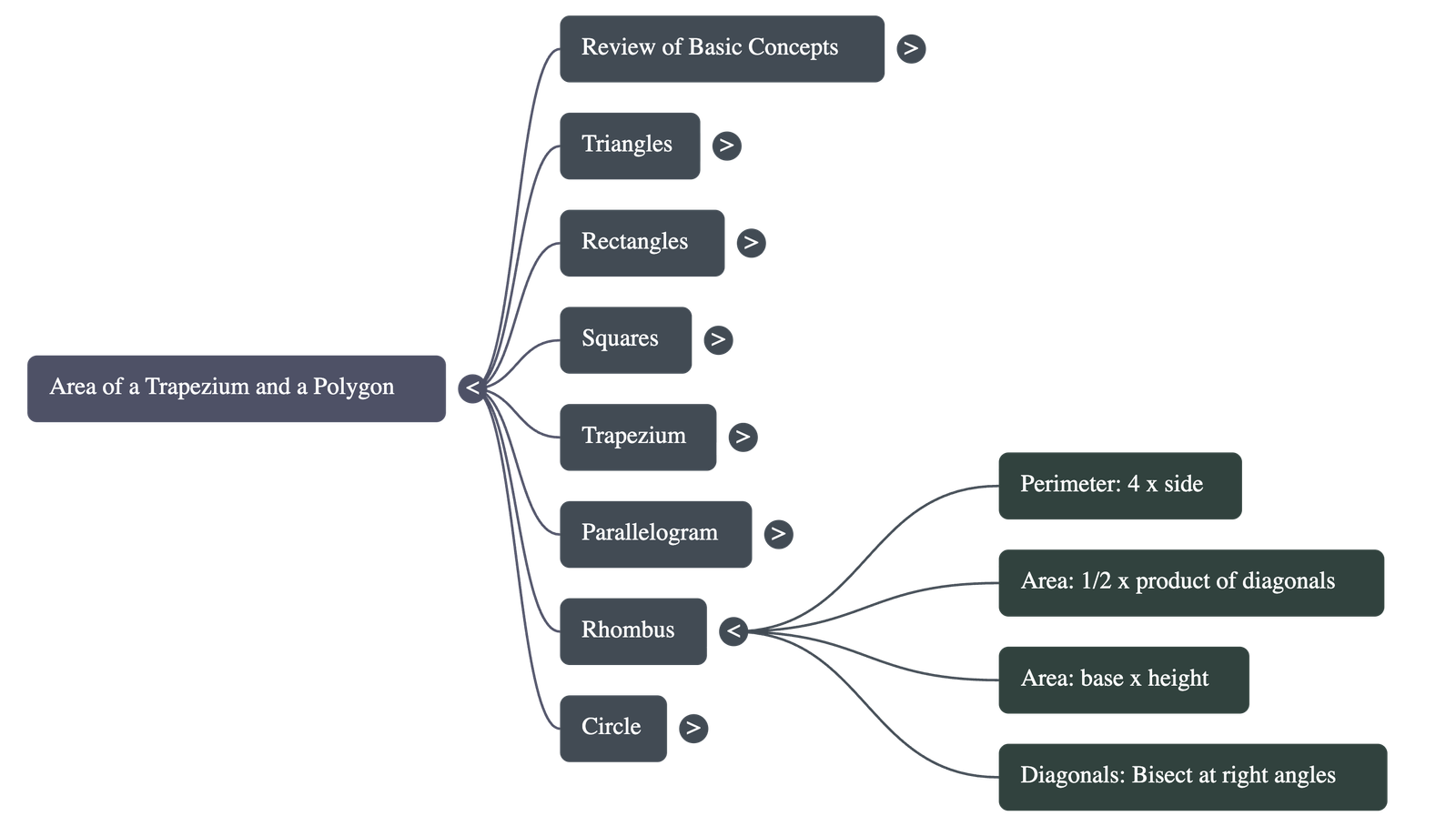
• Rhombus: A parallelogram with all sides equal.
  Area = 1/2 × product of diagonals (d1 × d2)
  Area = base × height
  Note: Diagonals of a rhombus bisect each other at right angles (90°).

5. Circles

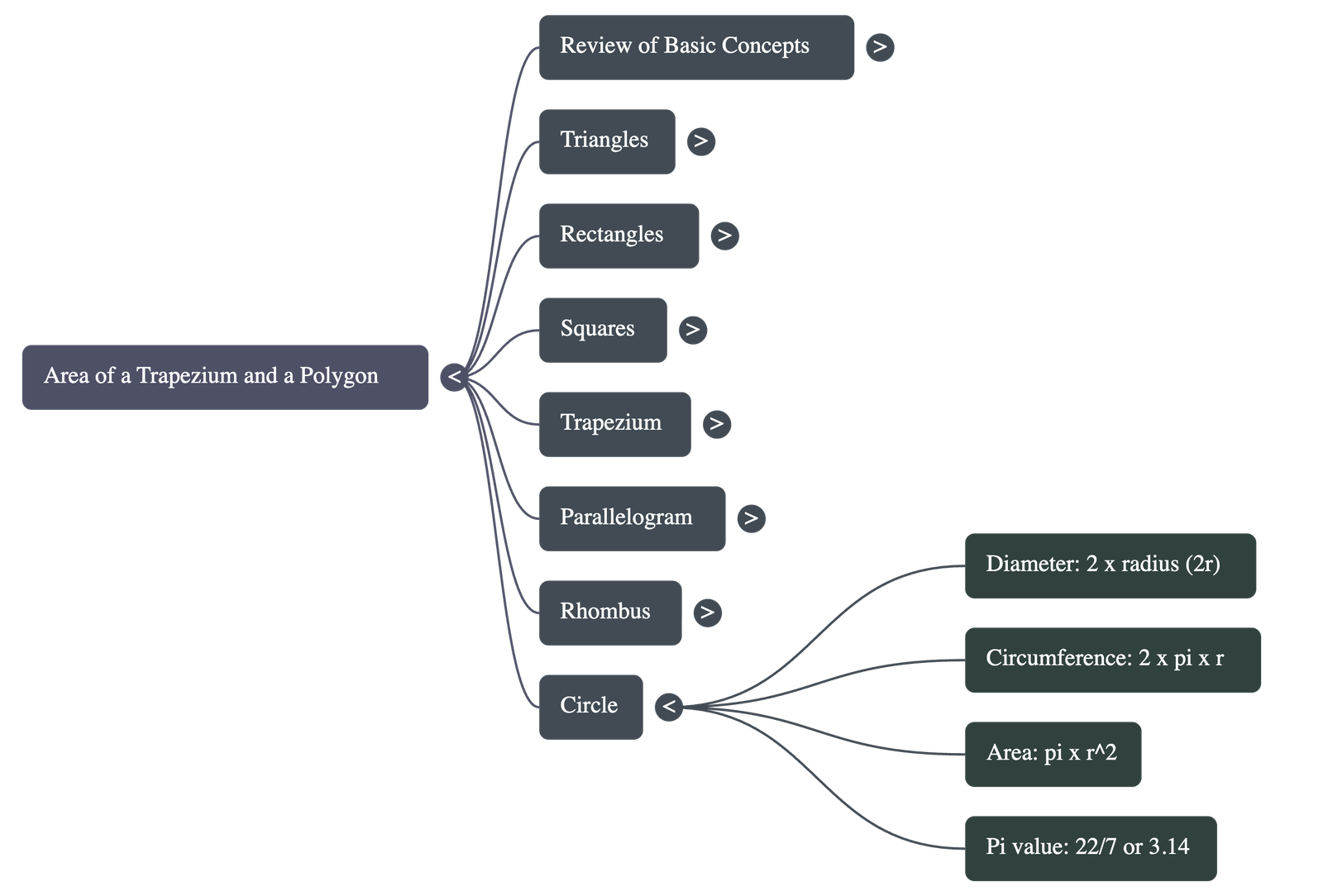
• Diameter (d): Twice the length of the radius (r).
• Circumference (C): The perimeter of a circle.
  Circumference = 2πr (where π ≈ 22/7 or 3.14)
• Area: The surface enclosed by the circle.
  Area = πr²

6. Practical Applications

• The sources discuss calculating the area of paths by subtracting the area of the inner rectangle/square from the outer one.
• Costing: To find the total cost for flooring, tiling, or levelling, the area is multiplied by the rate per unit area.
• Wheel Rotations: The distance travelled by a wheel in one revolution is equal to its circumference.