Summary of Chapter 5: Playing with Numbers

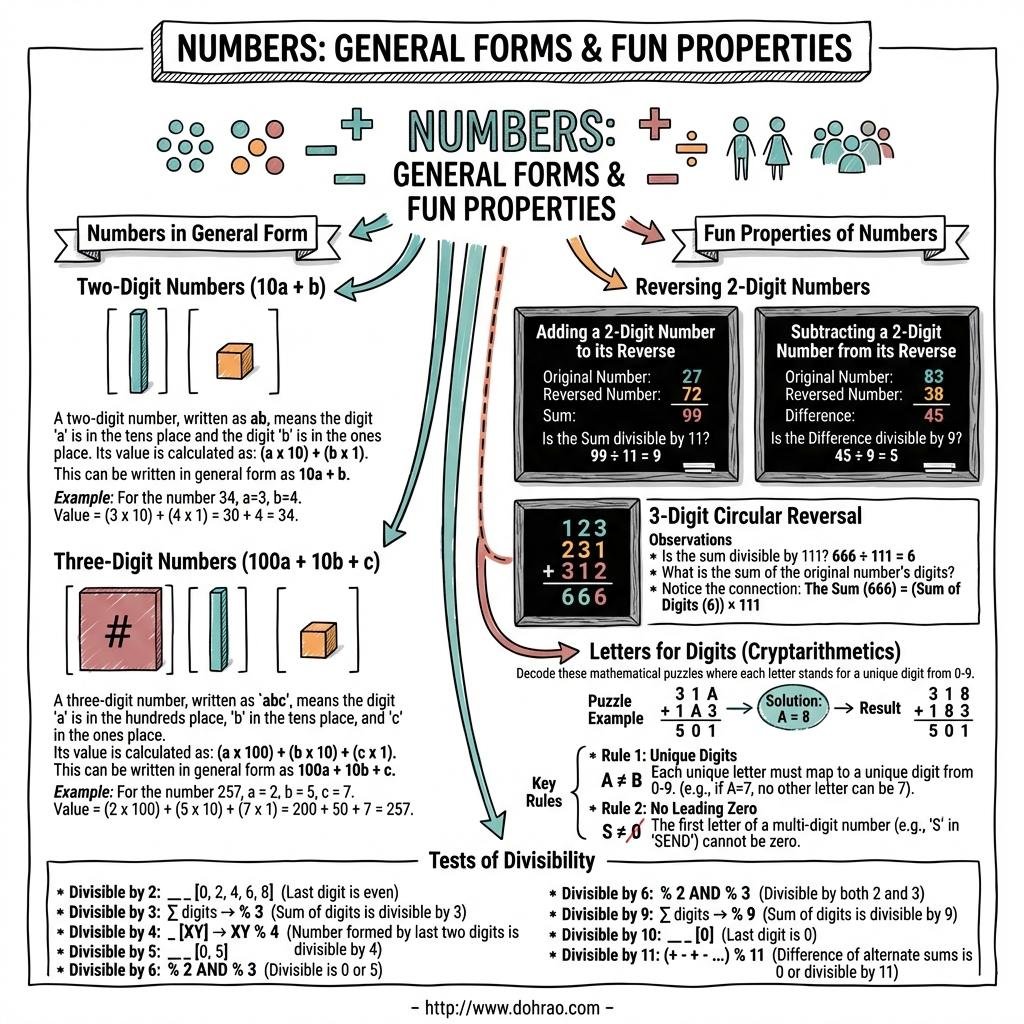
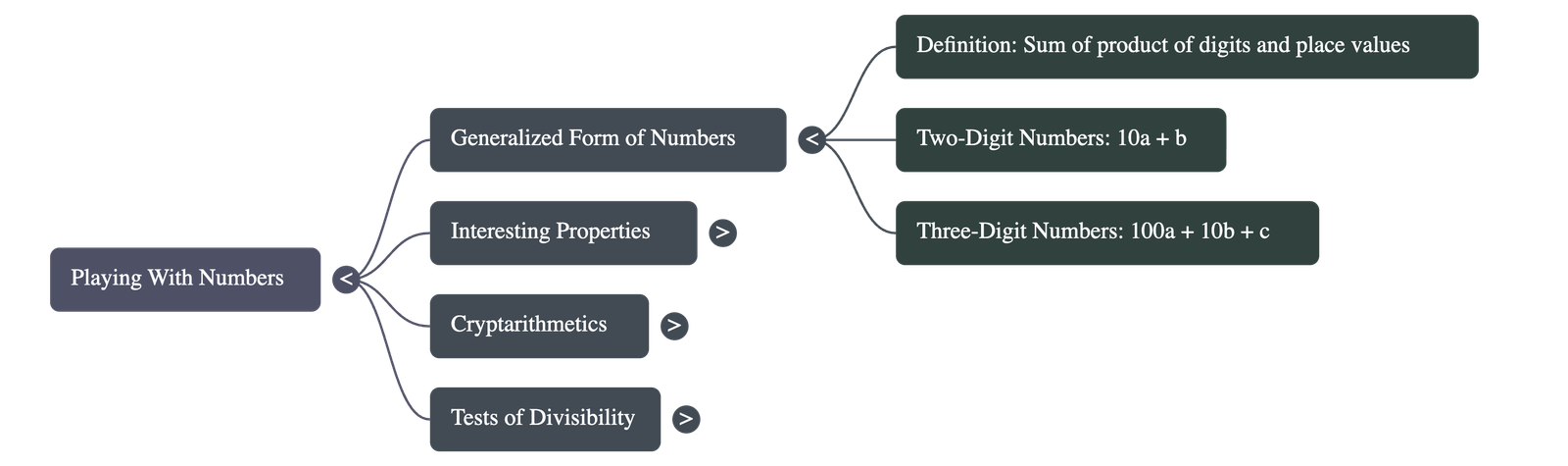
1. Generalized Form of Numbers

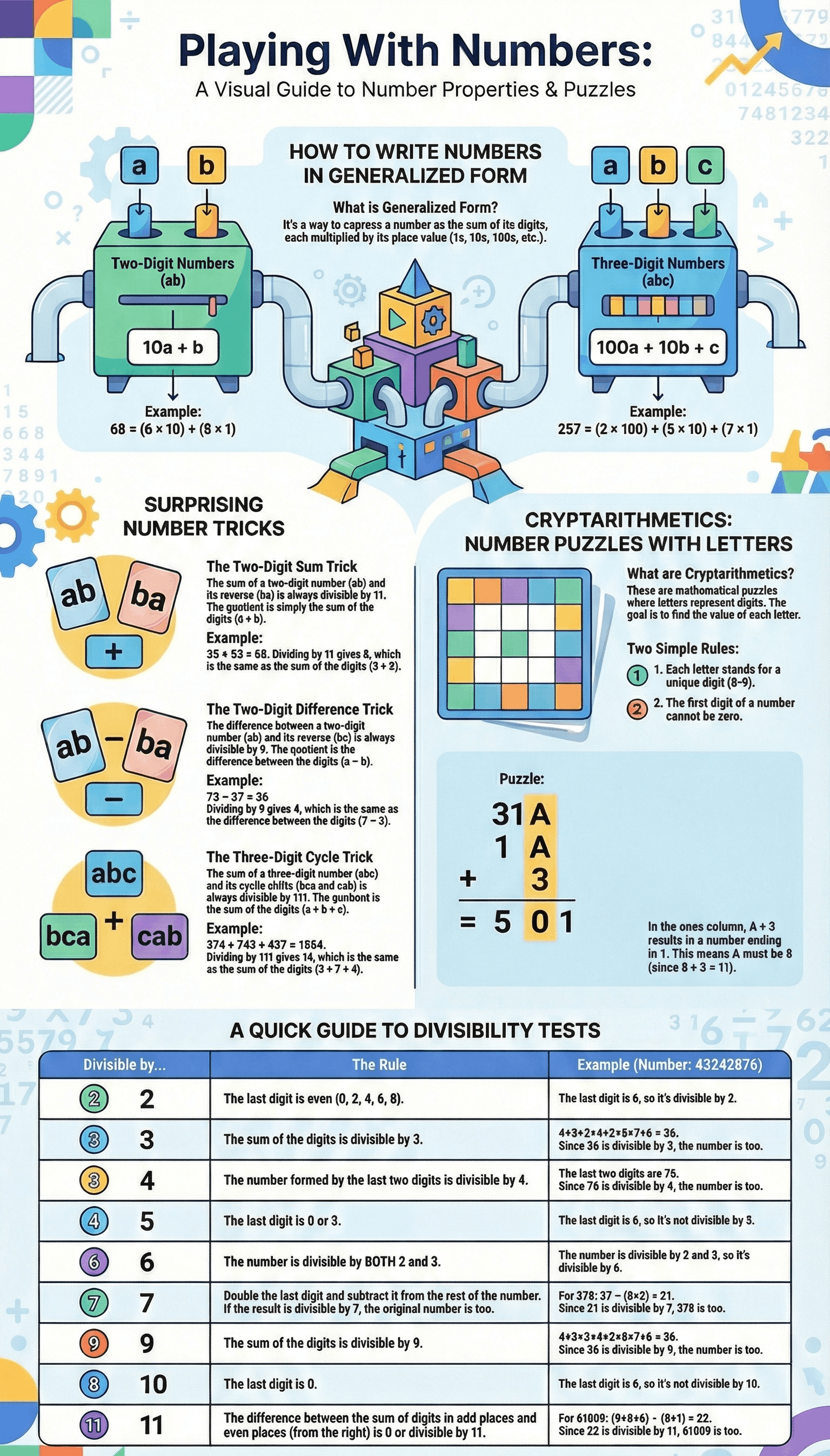
• Definition: A number is in generalized form when expressed as the sum of the products of its digits and their respective place values.
• Two-Digit Numbers: A number ab is written as 10a + b, where a is the tens digit (1-9) and b is the units digit (0-9).
• Three-Digit Numbers: A number abc is written as 100a + 10b + c, where a is the hundreds digit (1-9), b is the tens digit (0-9), and c is the units digit (0-9).

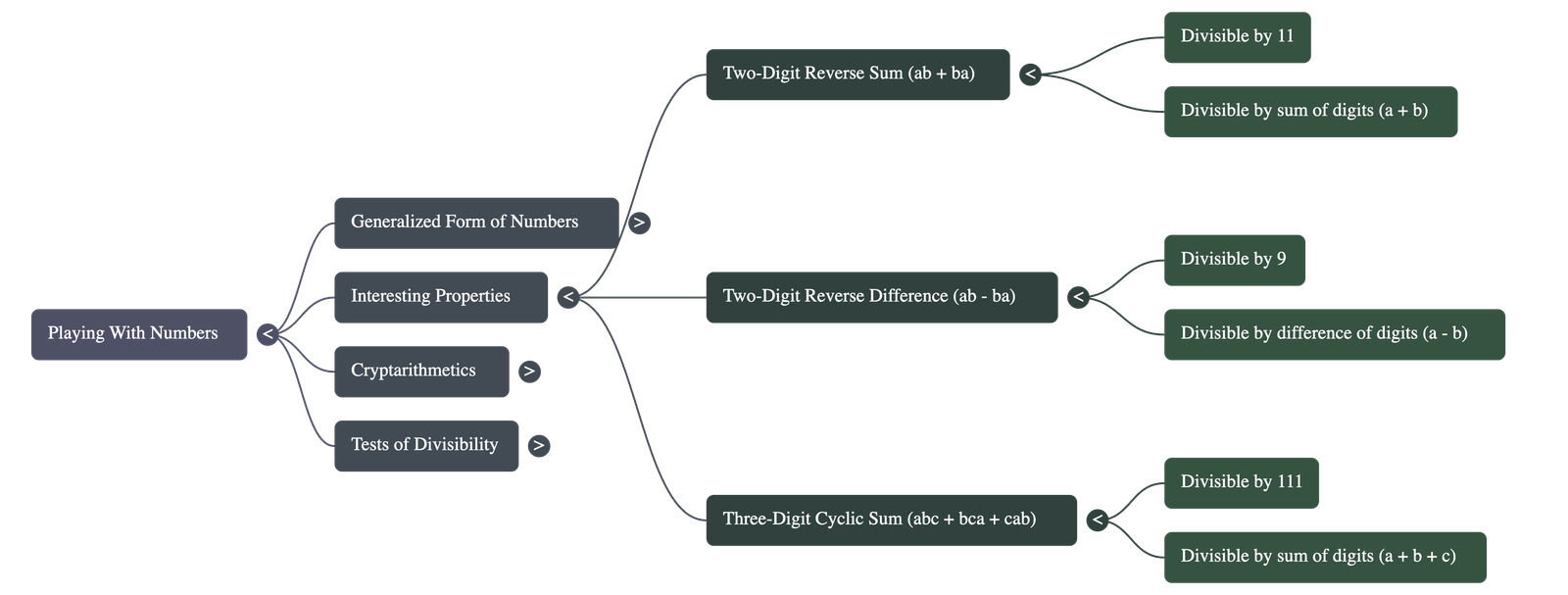
2. Interesting Number Properties

• Sum of Reversed Two-Digit Numbers: The sum of a two-digit number ab and the number obtained by reversing its digits ba (i.e., 11a + 11b) is always divisible by 11 and the sum of its digits (a + b).
• Difference of Reversed Two-Digit Numbers: The difference between a two-digit number ab and its reverse ba is always divisible by 9 and the difference between its digits.
• Cyclic Three-Digit Numbers: The sum of a three-digit number abc and its cyclic permutations (bca and cab) is always divisible by 111 and the sum of the digits (a + b + c). It is also divisible by 37, since 111 = 3 × 37.

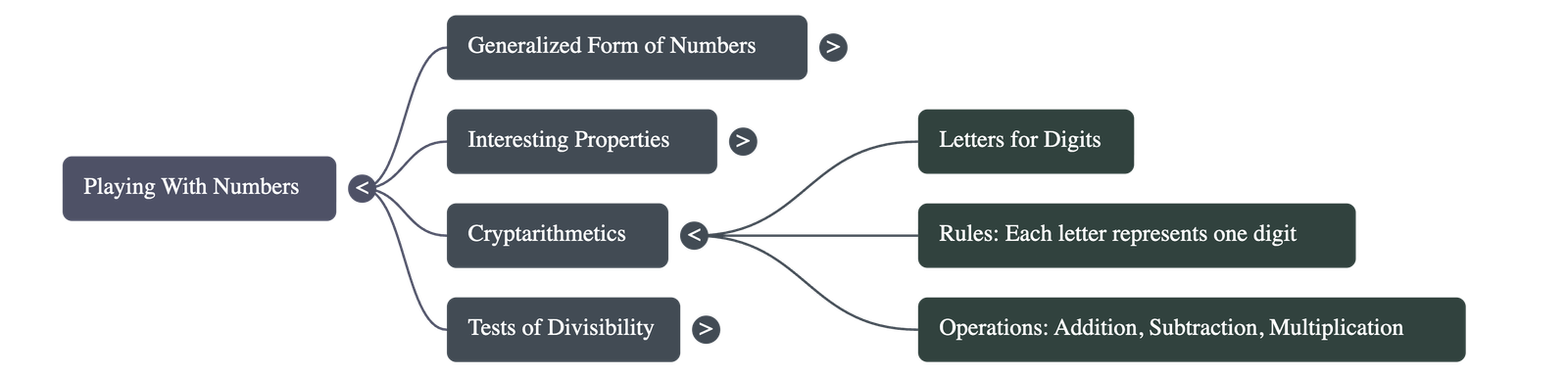
3. Letters for Digits (Cryptarithmetics)

• The Concept: This is a mathematical puzzle where letters represent digits. The goal is to determine which letter stands for which digit.
• The Rules:
  • Each letter in the puzzle must stand for only one digit.
  • Each digit must be represented by only one letter.
  • The first digit of a number cannot be zero.
  • Calculations must follow standard arithmetic rules for addition and multiplication, including carry-overs.

4. Tests of Divisibility

The chapter provides rules to check divisibility without performing full long division:

• Divisibility by 10: The number must end with the digit 0.
• Divisibility by 5: The units digit must be either 0 or 5.
• Divisibility by 2: The units digit must be an even number (0, 2, 4, 6, or 8).
• Divisibility by 9: The sum of the digits of the number must be divisible by 9.
• Divisibility by 3: The sum of the digits of the number must be divisible by 3.
• Divisibility by 6: The number must be divisible by both 2 and 3.
• Divisibility by 4: The number formed by the last two digits (tens and units) must be divisible by 4.
• Divisibility by 11: The difference between the sum of digits in odd places and the sum of digits in even places must be either 0 or a multiple of 11.
• Divisibility by 7: Double the units digit and subtract it from the remaining number. If the result is divisible by 7, the original number is divisible by 7.