This chapter explores the methods of breaking down algebraic expressions into their constituent factors. Below is a concise summary of the key concepts and techniques covered:

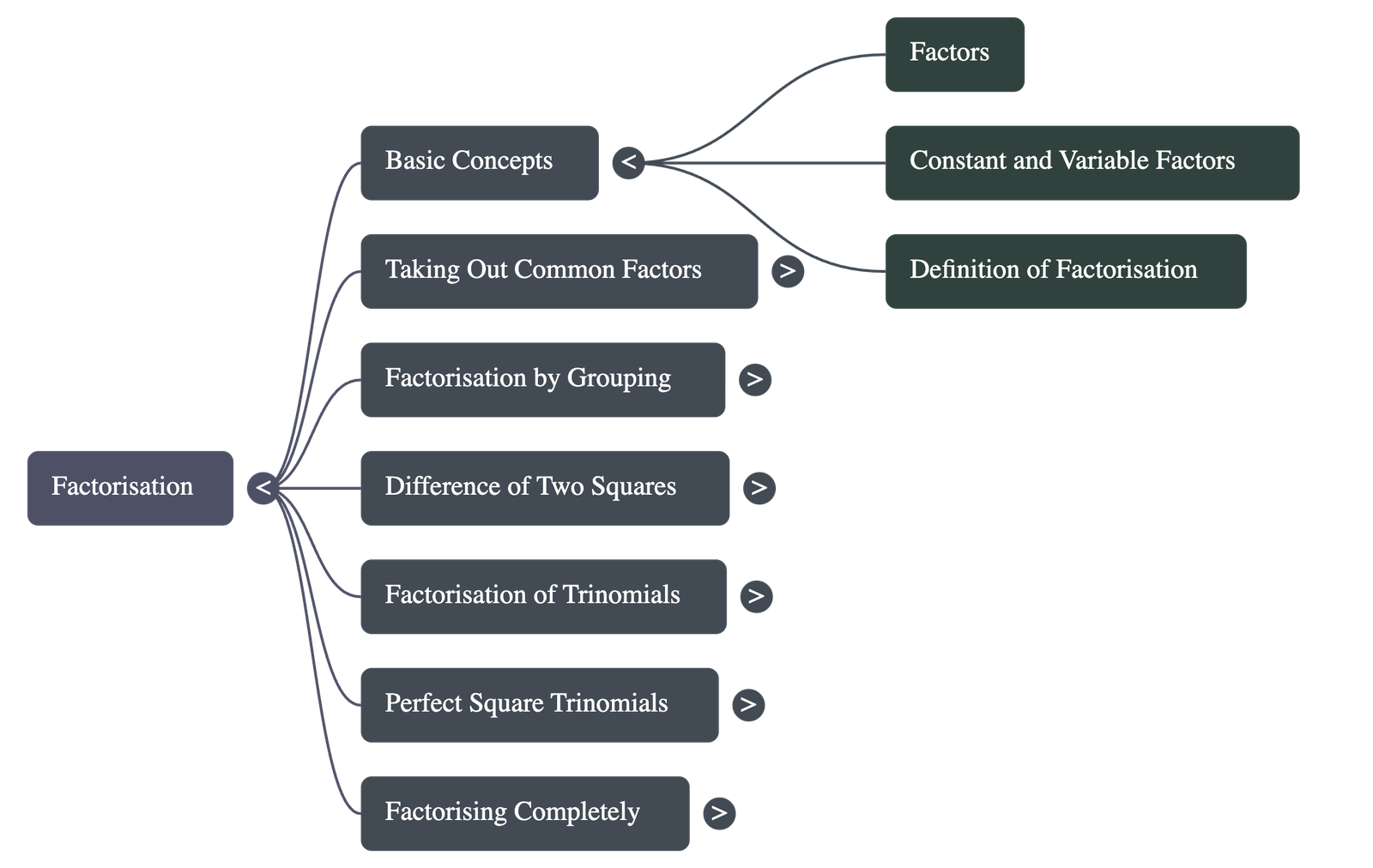
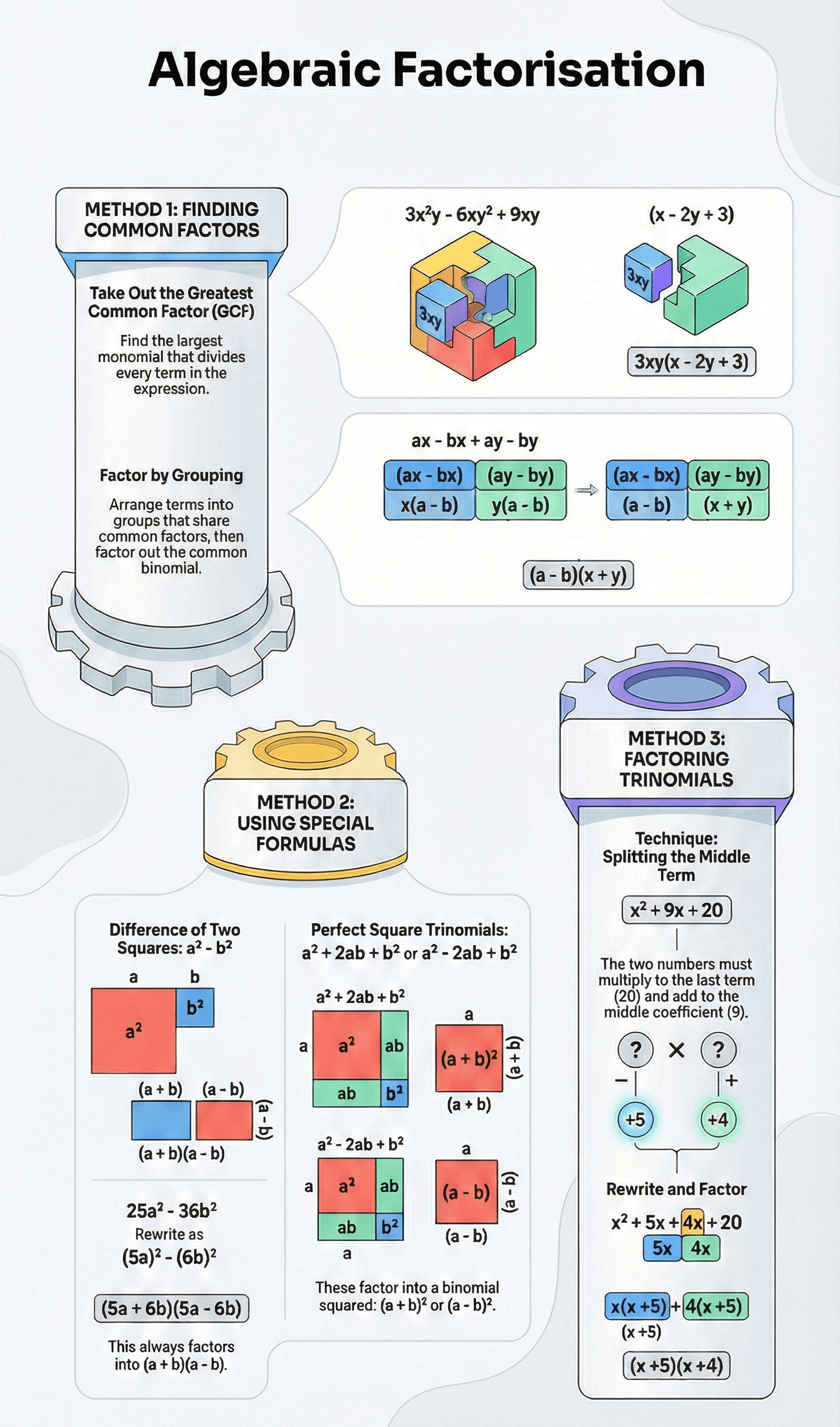
• 1. Definition of Factorisation
  Factorisation is the process of finding two or more algebraic expressions whose product is equal to a given expression. Each individual constant or variable that forms the product is known as a factor.
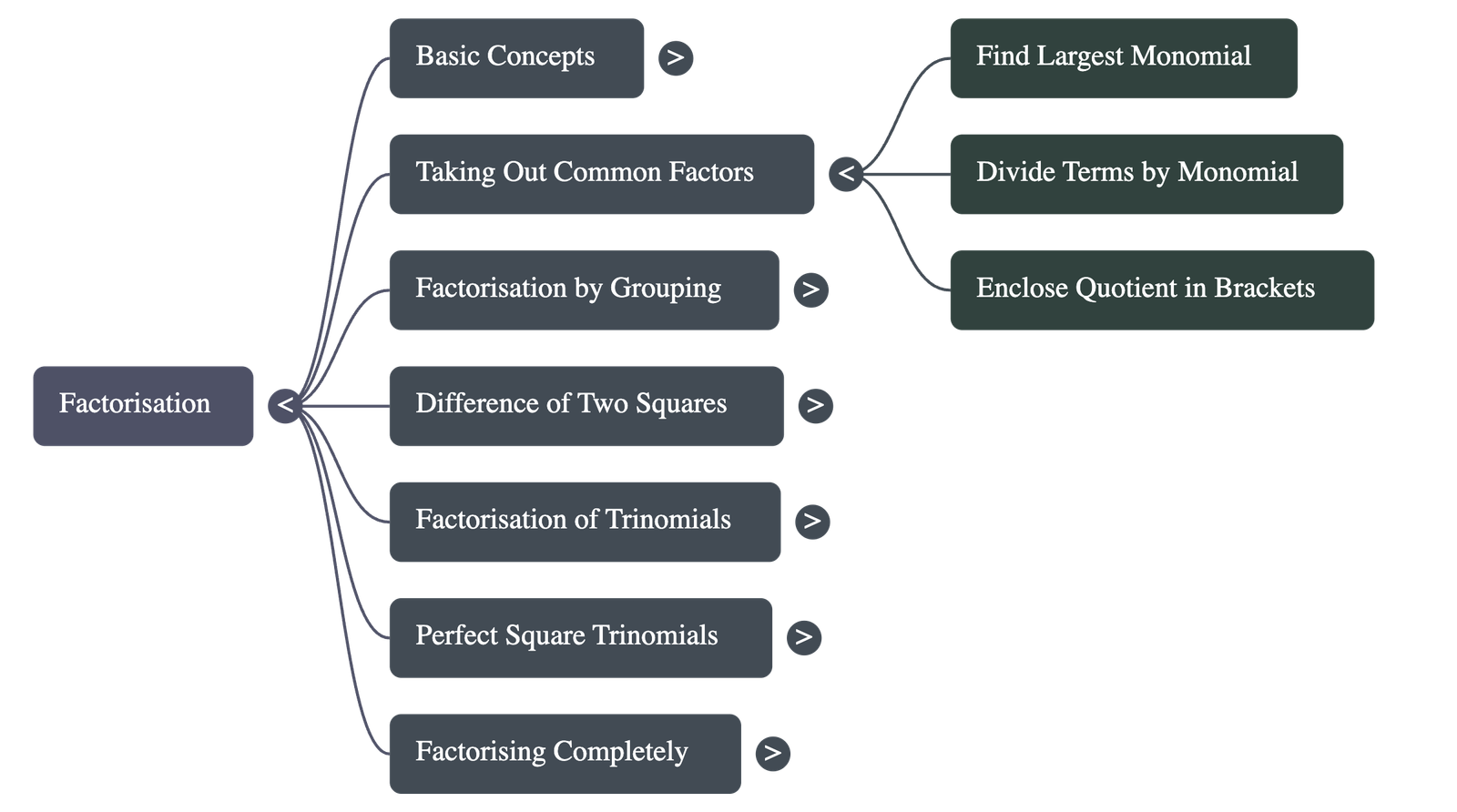
• 2. Taking Out Common Factors
  The most basic method of factorisation involves identifying the largest monomial that divides every term of the polynomial. This common factor is placed outside a set of brackets, while the remaining quotients for each term are placed inside.
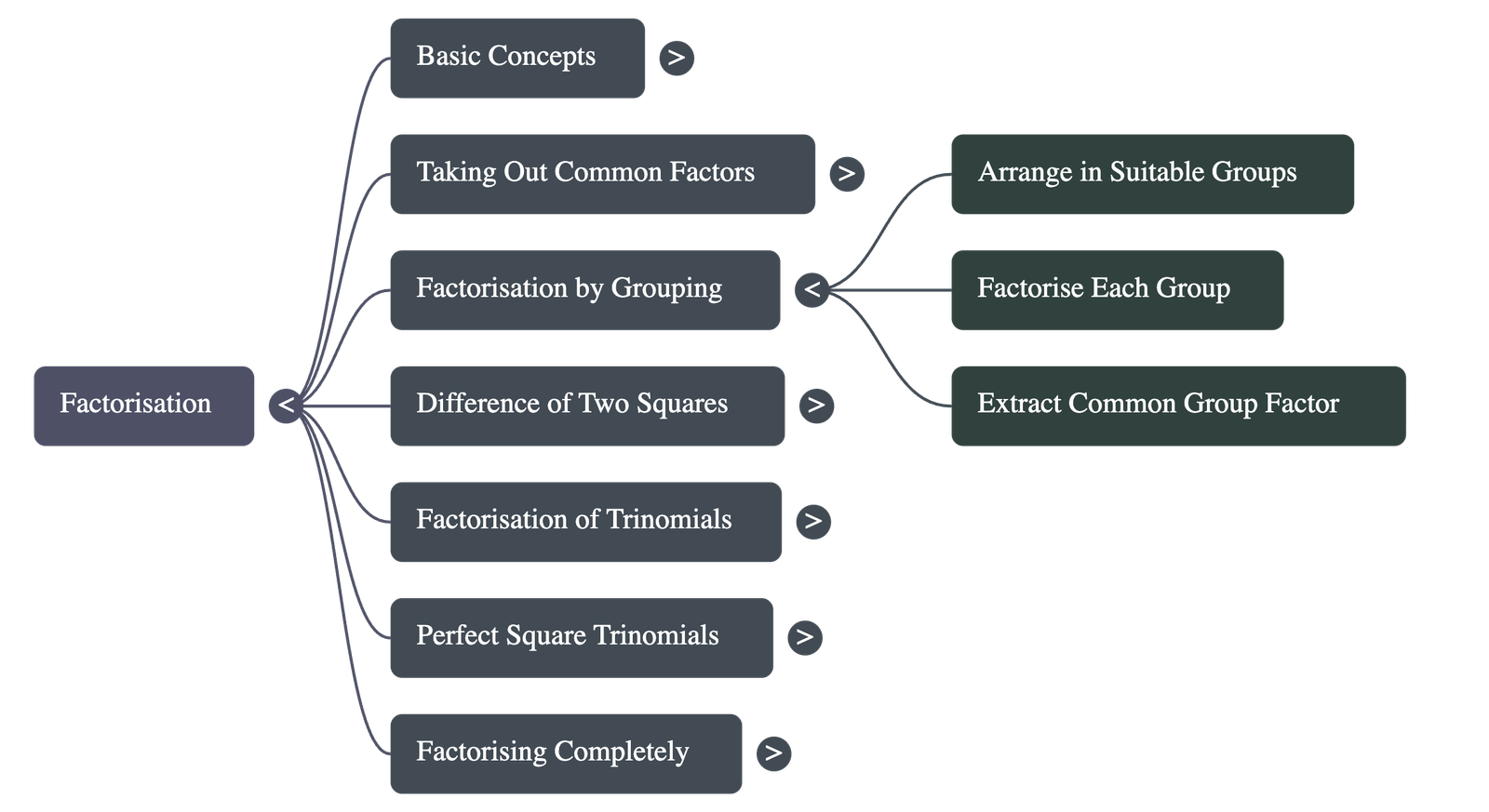
• 3. Factorisation by Grouping
  For expressions with an even number of terms, terms can be rearranged into suitable groups where each group shares a common factor. Once the groups are factorised individually, a common binomial factor can often be extracted from the resulting terms.
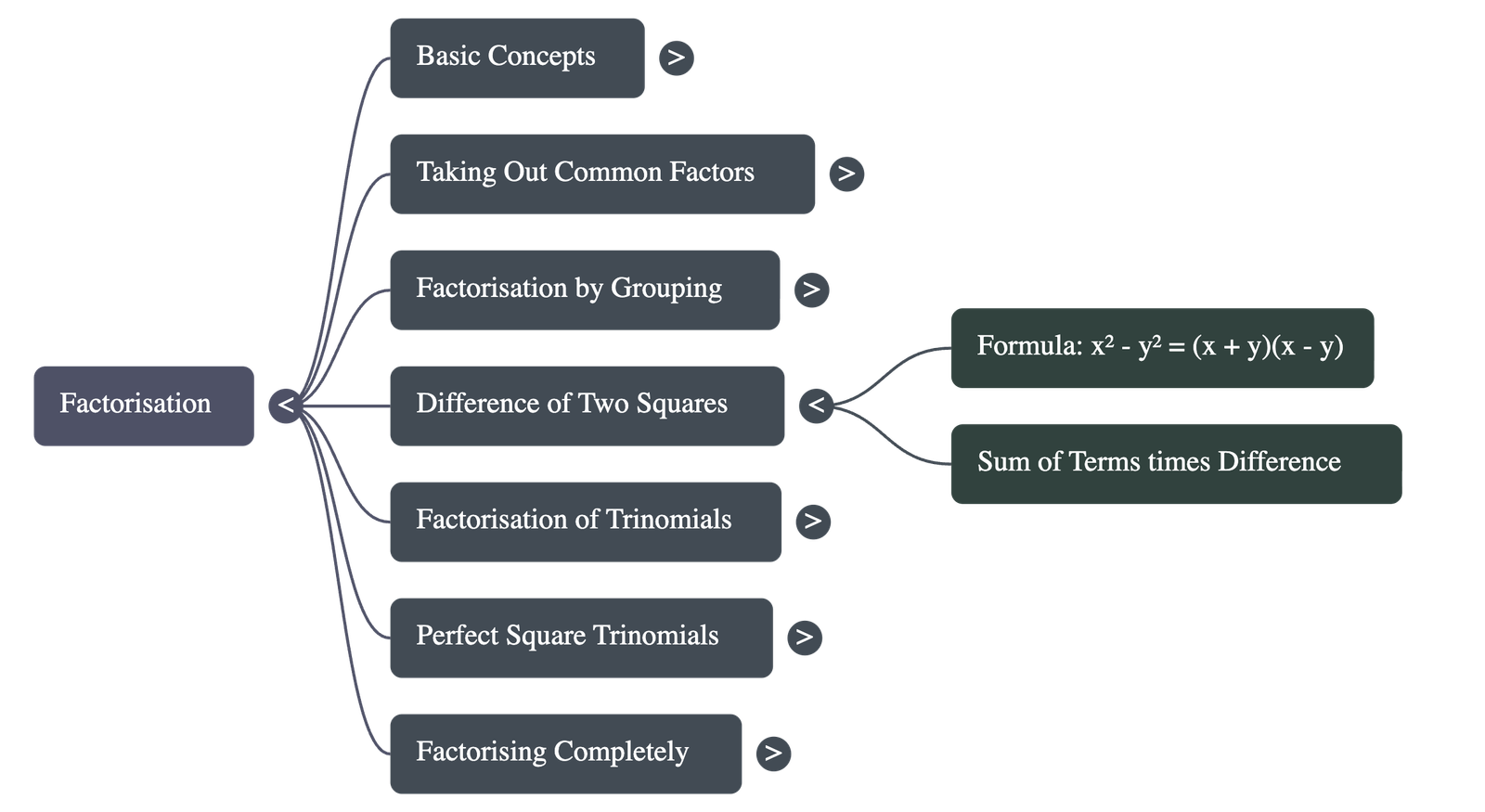
• 4. Difference of Two Squares
  Using the algebraic identity a² - b² = (a + b)(a - b), any expression that can be written as the difference between two squares can be factorised into the product of the sum and the difference of the terms.
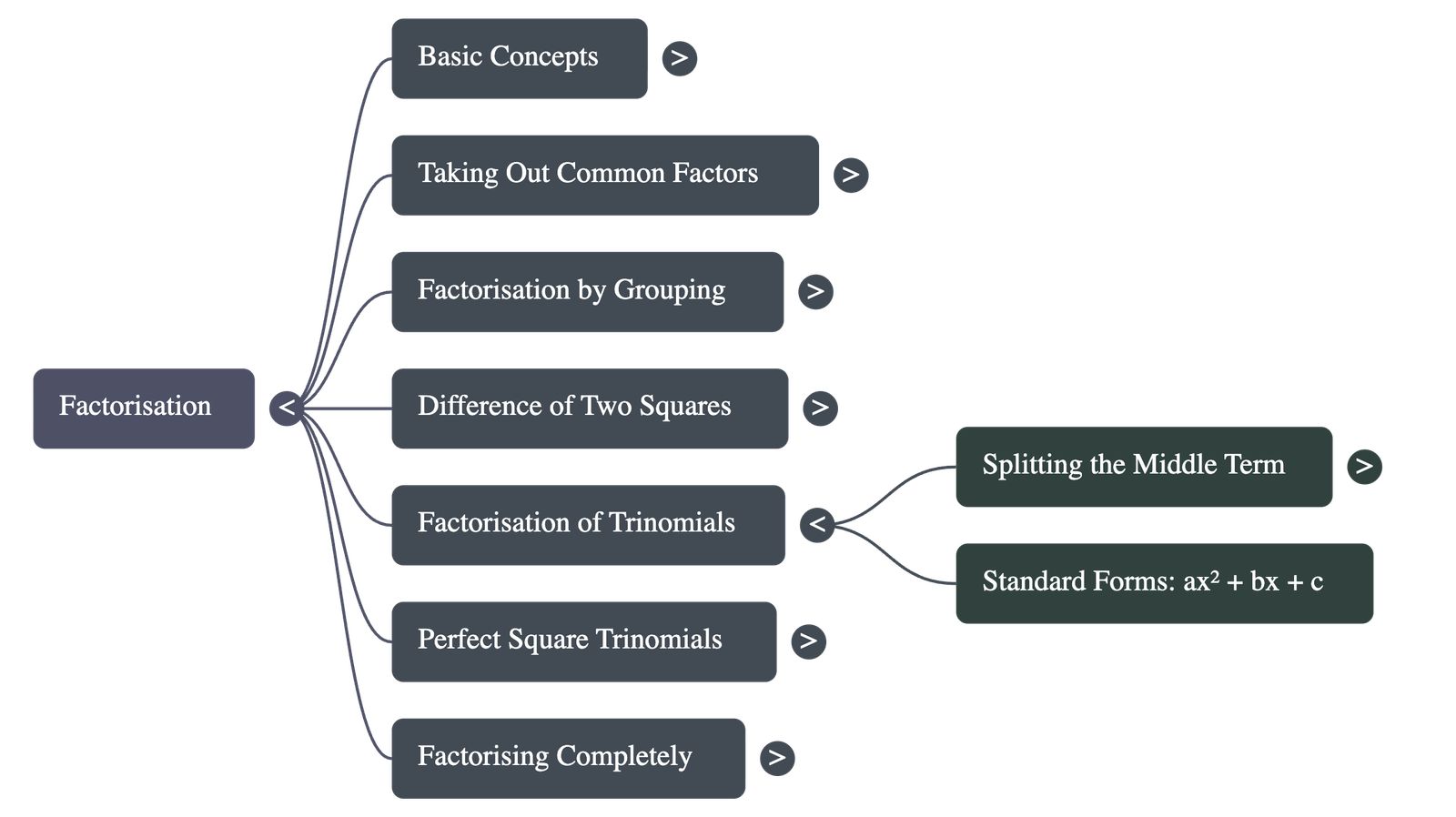
• 5. Factorisation of Trinomials (Splitting the Middle Term)
  To factorise a trinomial (e.g., ax² + bx + c), the middle term (b) is split into two parts. These two parts must have a sum equal to the middle term and a product equal to the product of the first and last terms (a × c).
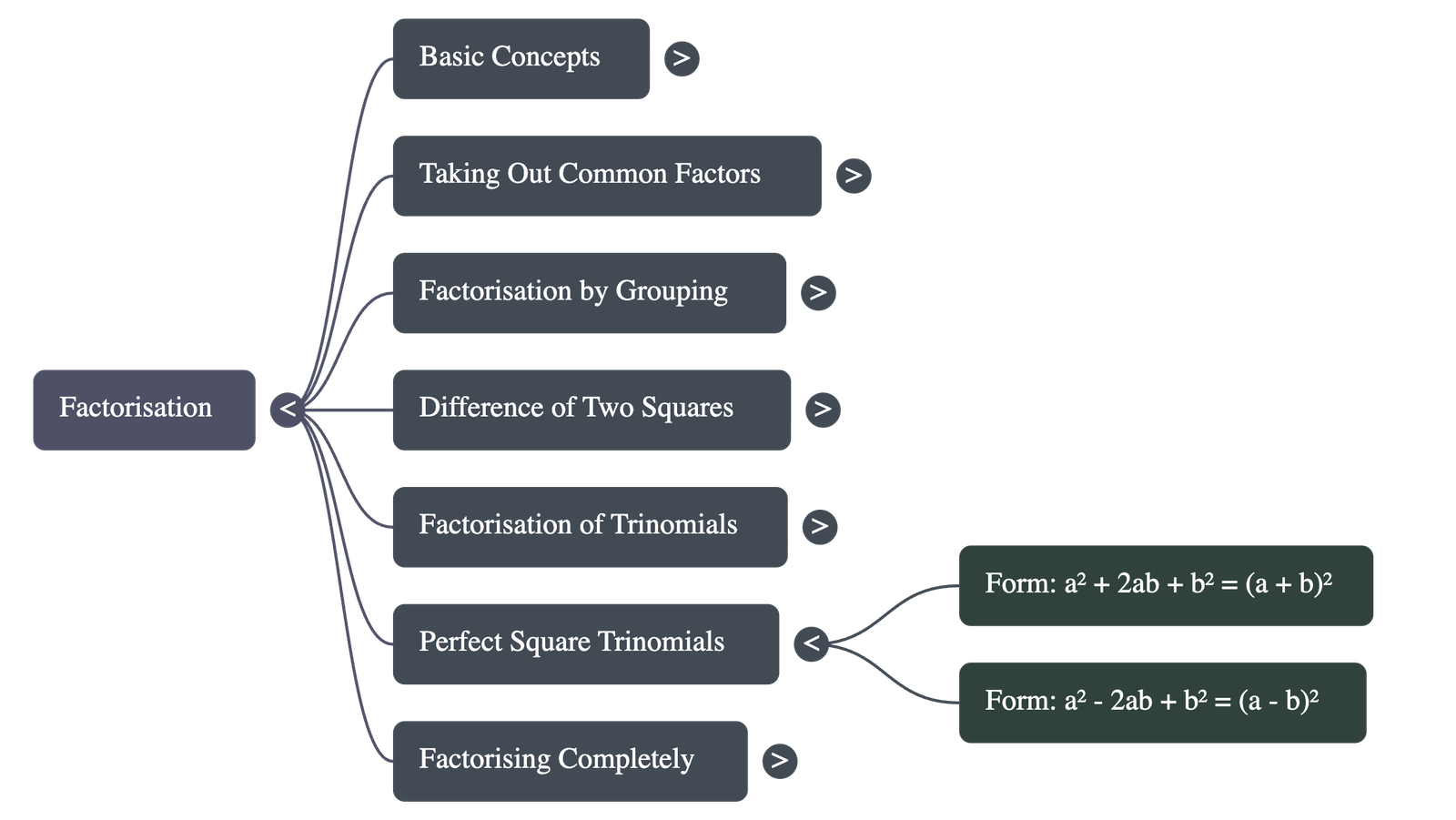
• 6. Perfect Square Trinomials
  Expressions that fit the patterns a² + 2ab + b² or a² - 2ab + b² are called perfect square trinomials. These can be simplified directly into (a + b)² or (a - b)² respectively.
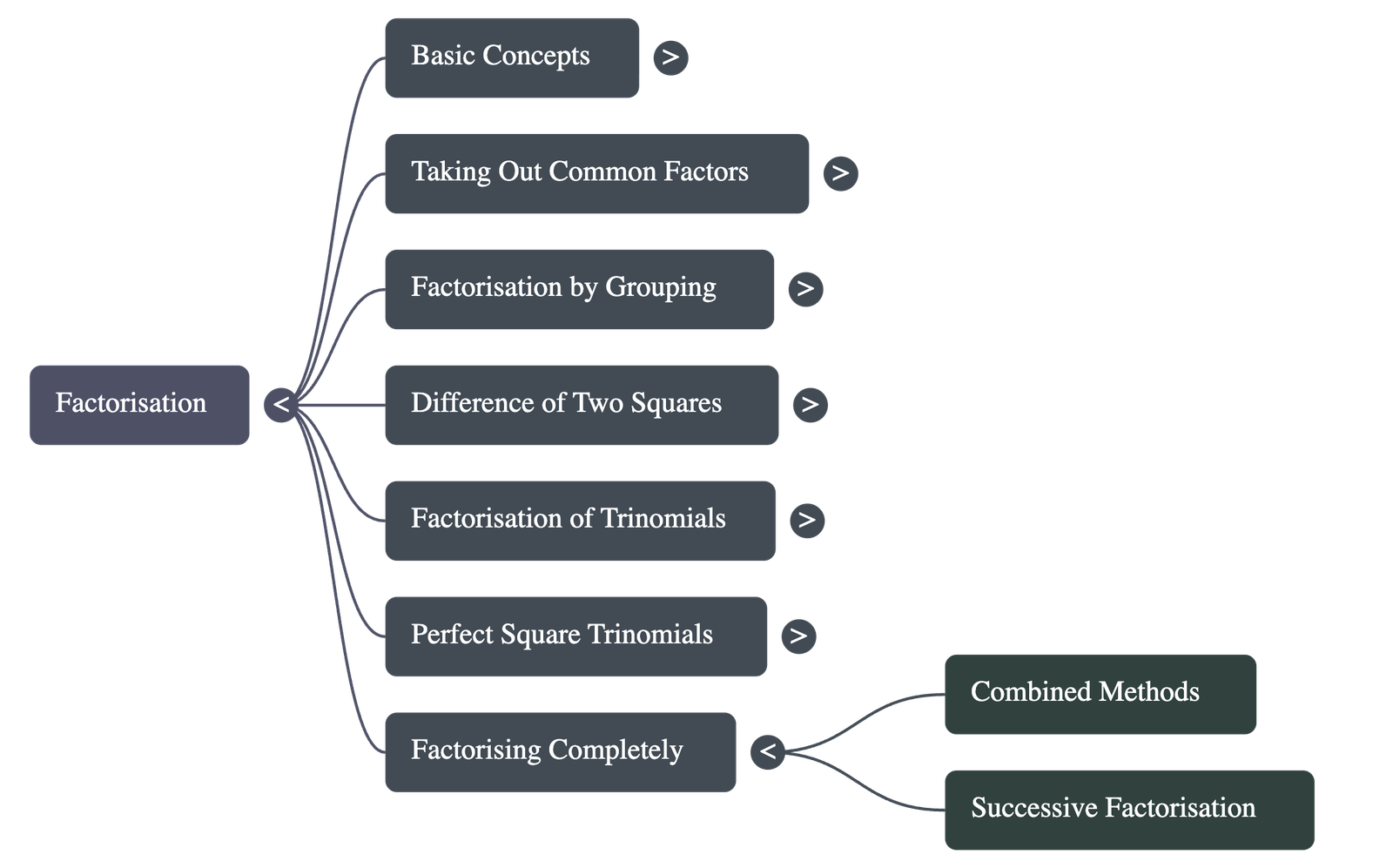
• 7. Factorising Completely
  Some complex expressions require multiple steps. This often involves first taking out a common factor and then applying other methods, such as splitting the middle term or using the difference of squares formula, to ensure the expression is broken down into its simplest possible factors.