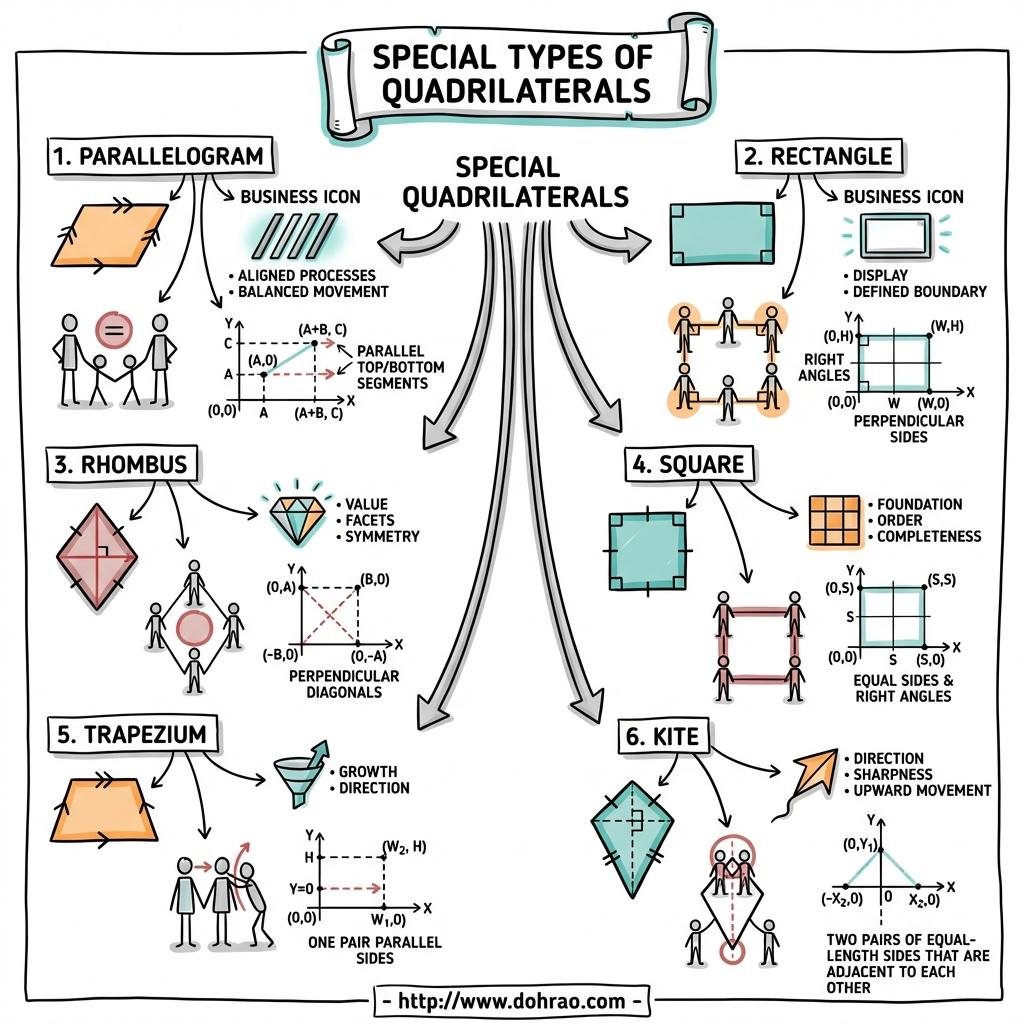
1. General Quadrilateral

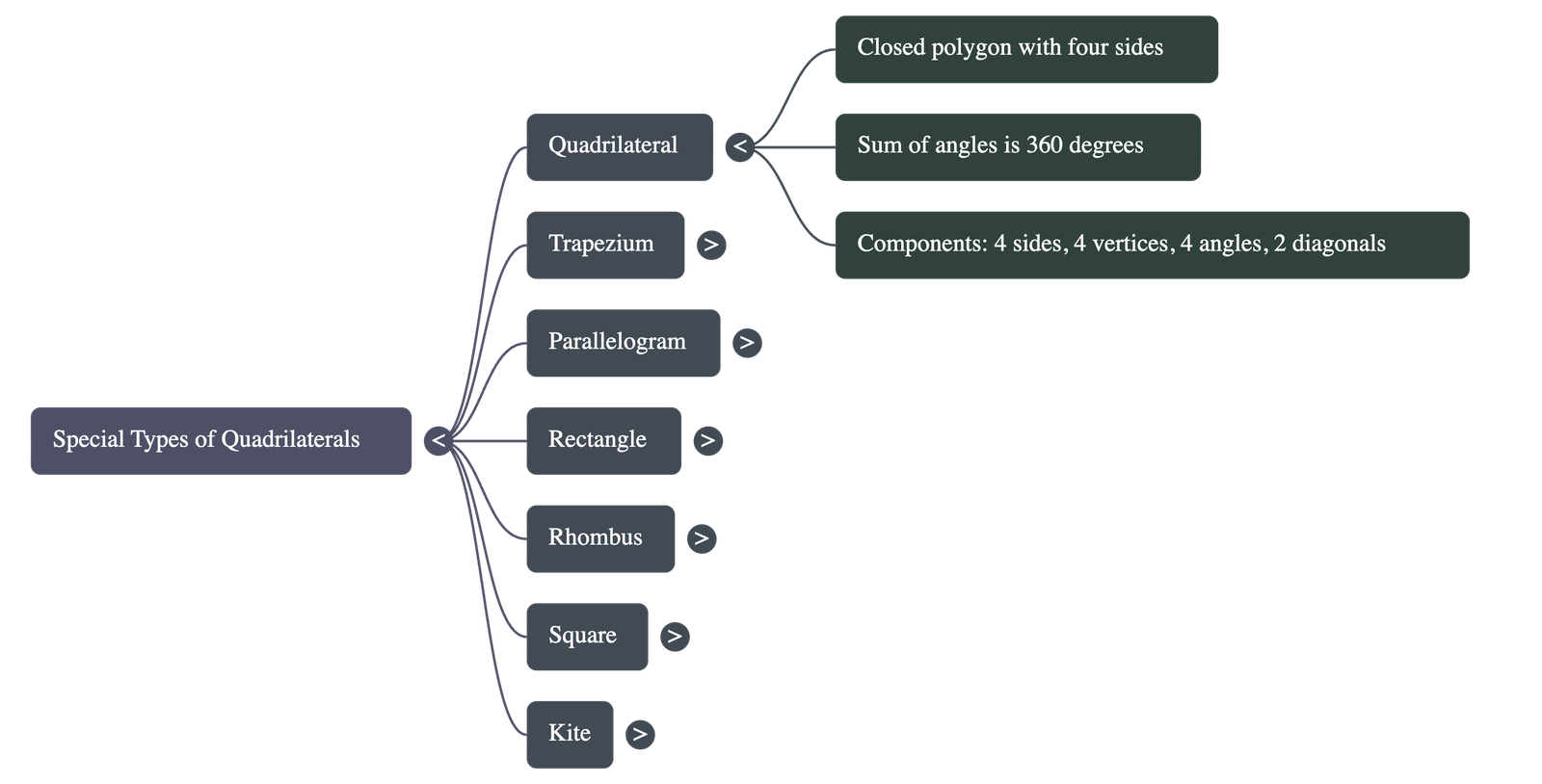
• A quadrilateral is a closed polygon with four sides.
• It consists of four vertices, four angles, and two diagonals.
• The sum of the interior angles of any quadrilateral is always 360° (equal to four right angles).

2. Trapezium

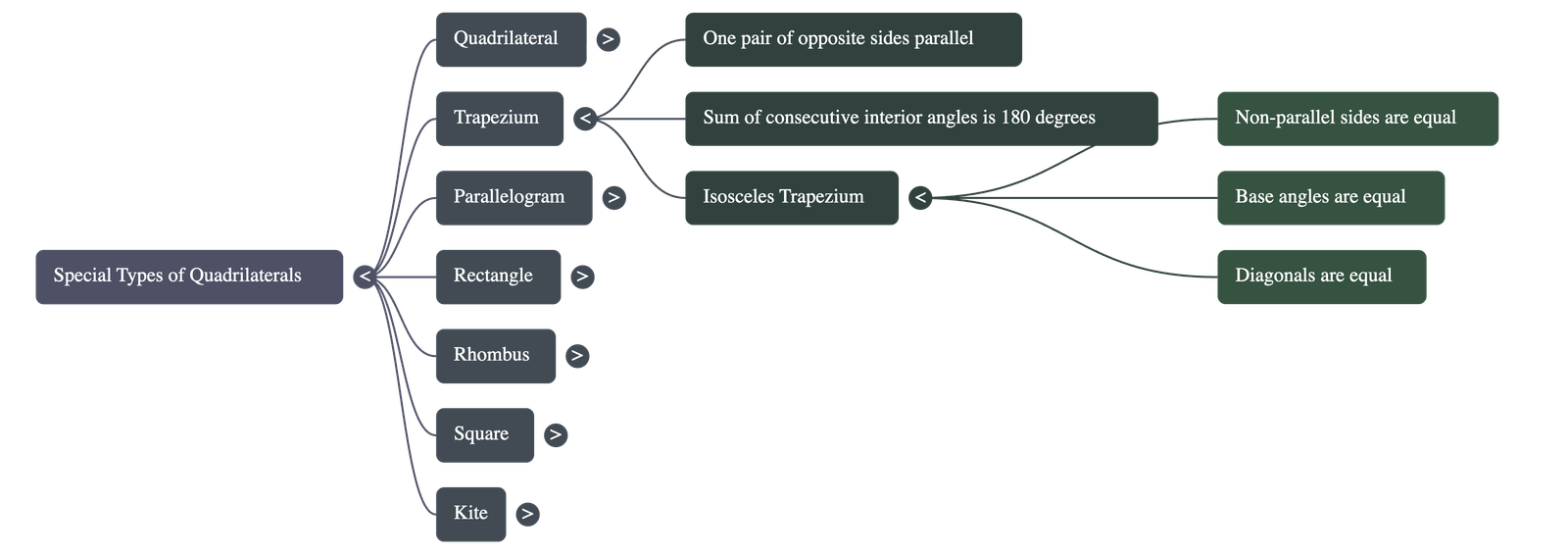
• A quadrilateral with one pair of opposite sides parallel and the other pair non-parallel.
• In a trapezium, the angles between a parallel side and a non-parallel side are supplementary (sum to 180°).
• Isosceles Trapezium: A specific type where the non-parallel sides are equal. In this case, the base angles are equal and the diagonals are of equal length.

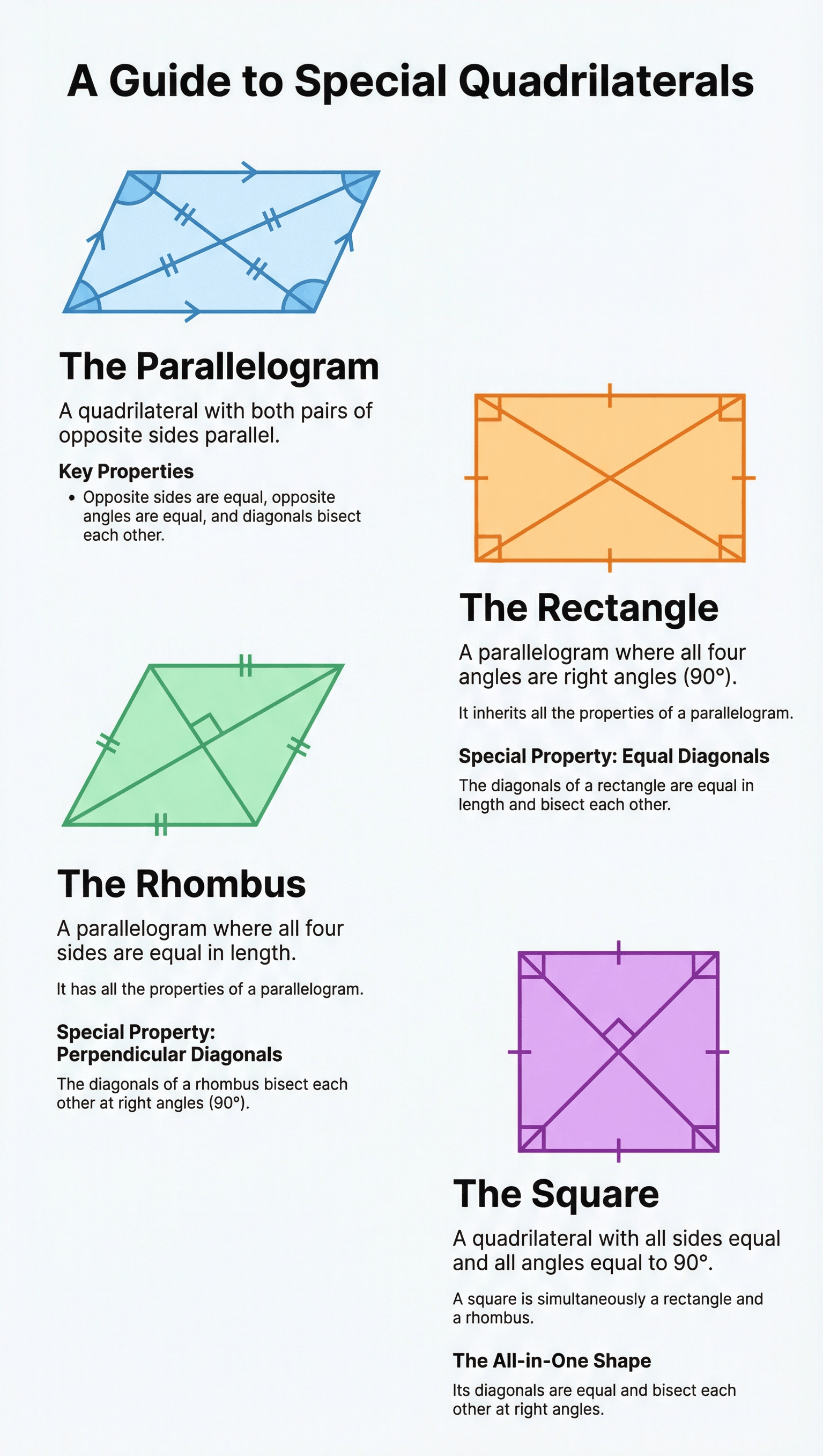
3. Parallelogram

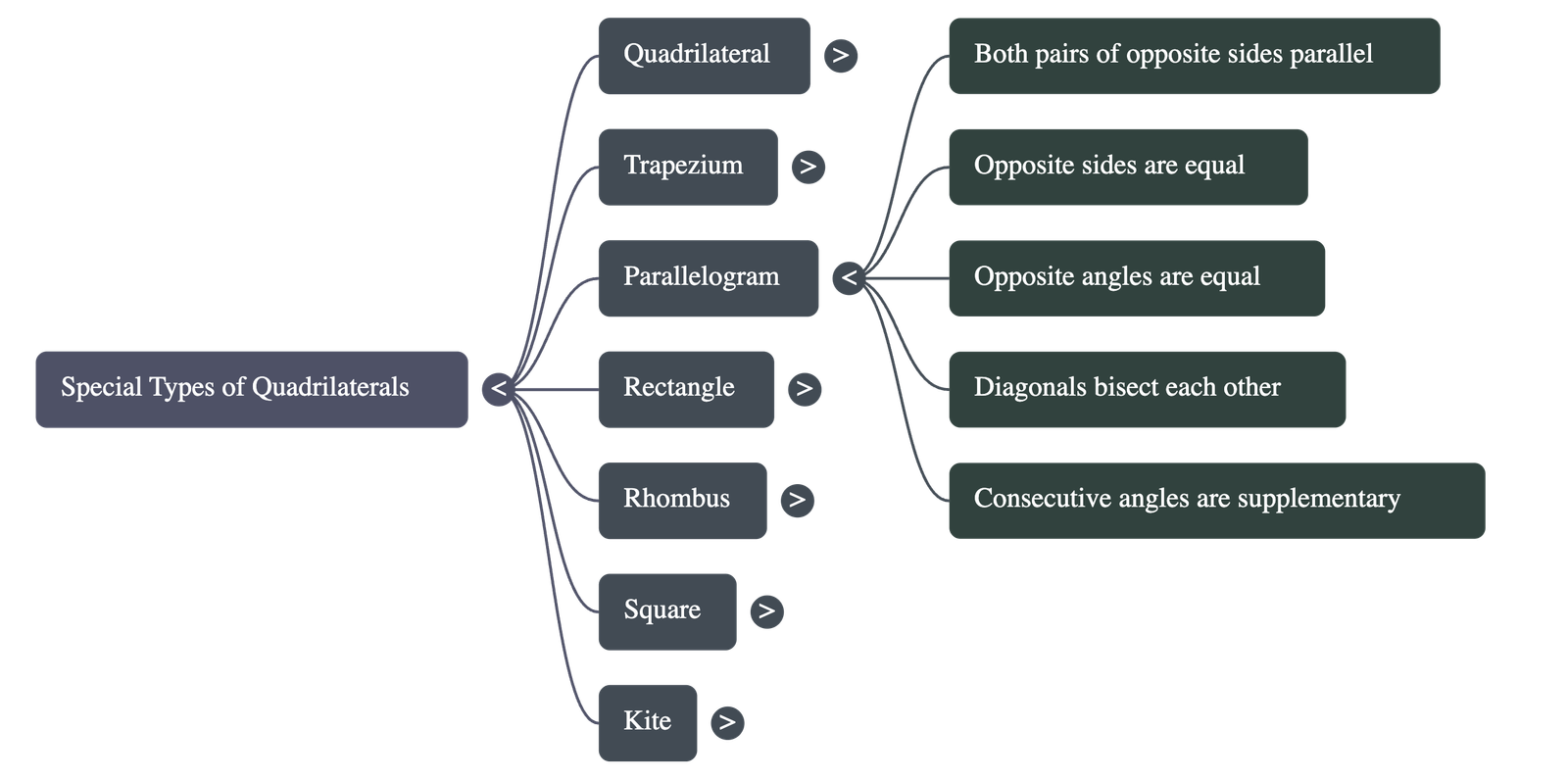
• A quadrilateral where both pairs of opposite sides are parallel.
• Key Properties:
  - Opposite sides are equal in length.
  - Opposite angles are equal.
  - Each diagonal bisects the parallelogram into two congruent triangles.
  - Diagonals bisect each other.
• To prove a quadrilateral is a parallelogram, one can show that opposite sides are equal, opposite angles are equal, diagonals bisect each other, or one pair of opposite sides is both equal and parallel.

4. Rectangle

• A parallelogram in which each angle is a right angle (90°).
• Since it is a parallelogram, its opposite sides are equal and parallel.
• A unique property of a rectangle is that its diagonals are equal and they bisect each other.

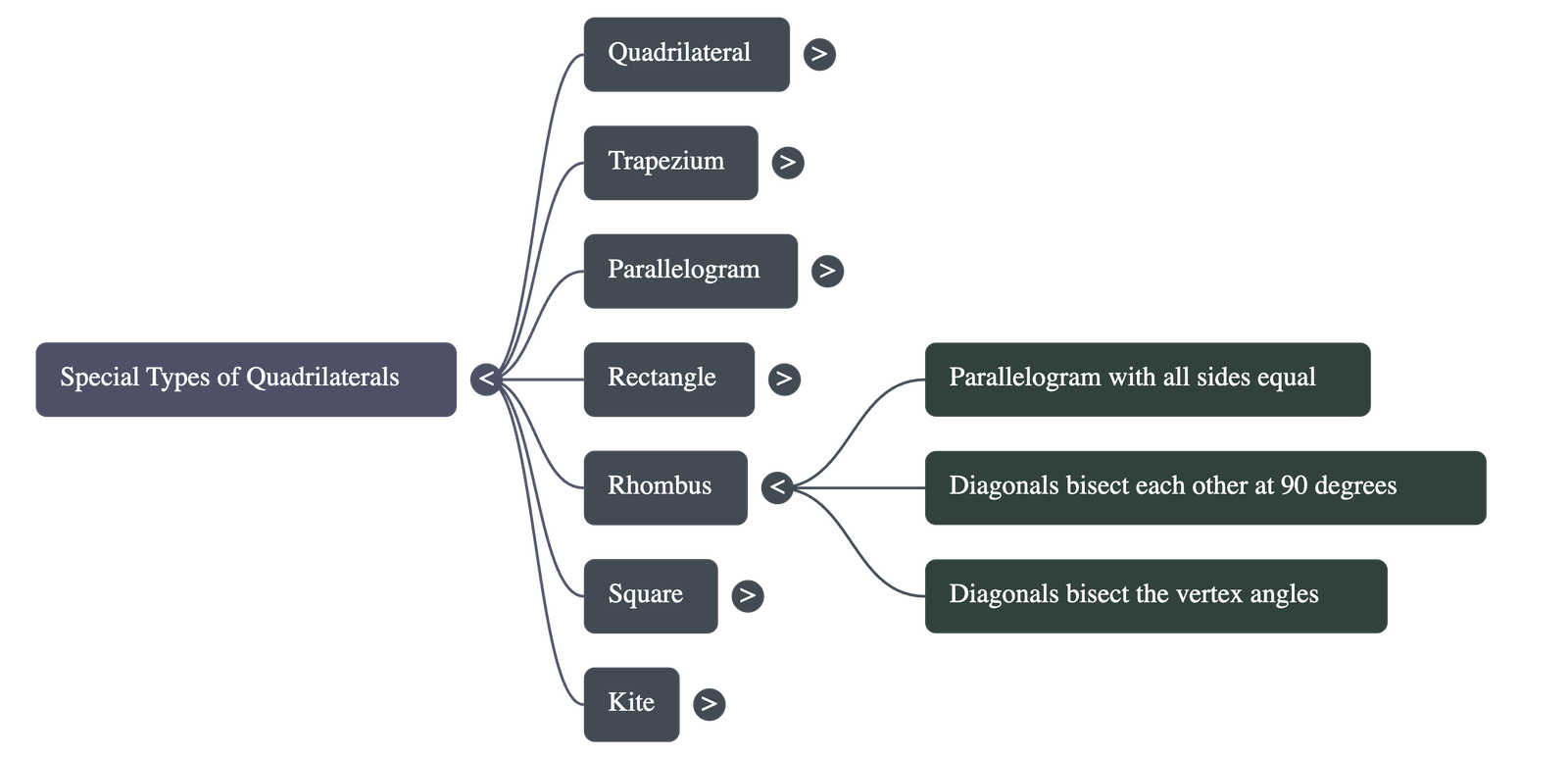
5. Rhombus

• A quadrilateral where all four sides are equal in length.
• It is a special type of parallelogram; therefore, its opposite angles are equal and opposite sides are parallel.
• Distinctive Property: The diagonals of a rhombus bisect each other at right angles (90°).

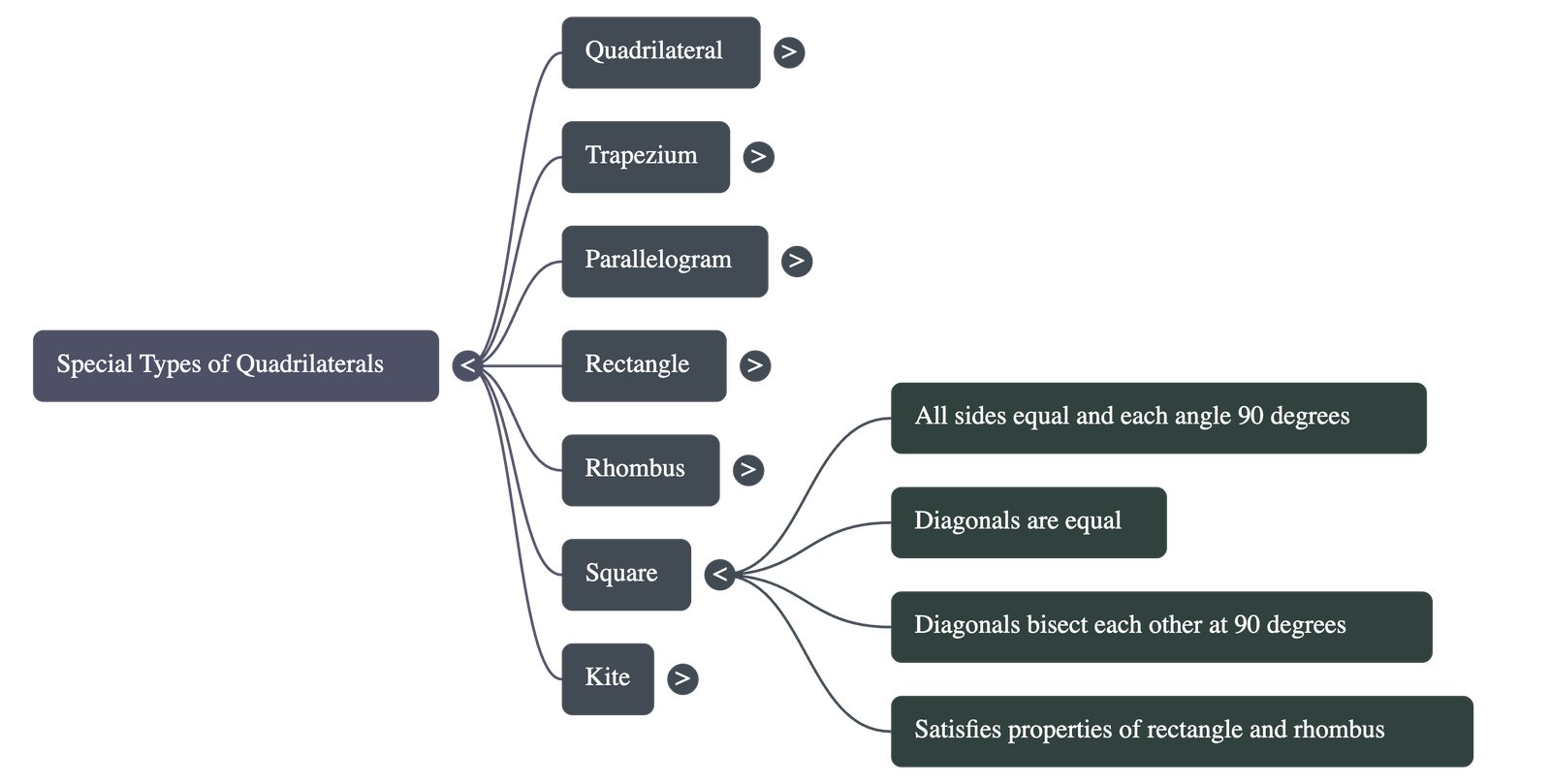
6. Square

• A quadrilateral where all sides are equal and each angle is 90°.
• A square is the most "complete" quadrilateral, satisfying the properties of a rectangle, a rhombus, and a parallelogram.
• Diagonals: They are equal in length and bisect each other at right angles.

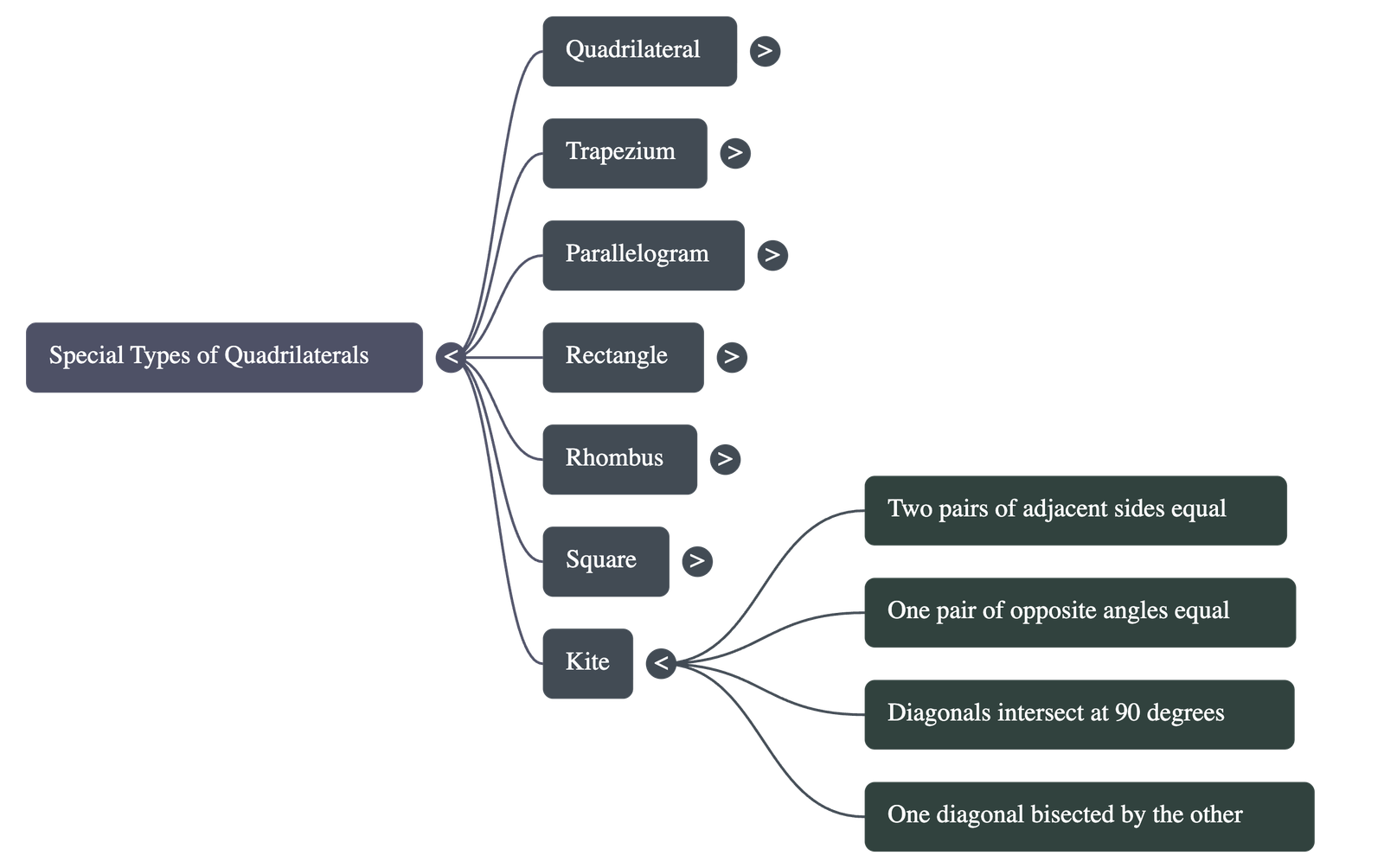
7. Kite

• A quadrilateral with two pairs of equal adjacent sides.
• Properties:
  - One pair of opposite angles is equal.
  - Diagonals intersect each other at right angles.
  - One diagonal is bisected by the other.
  - One diagonal bisects the interior angles at the vertices it joins.