1. Linear Symmetry

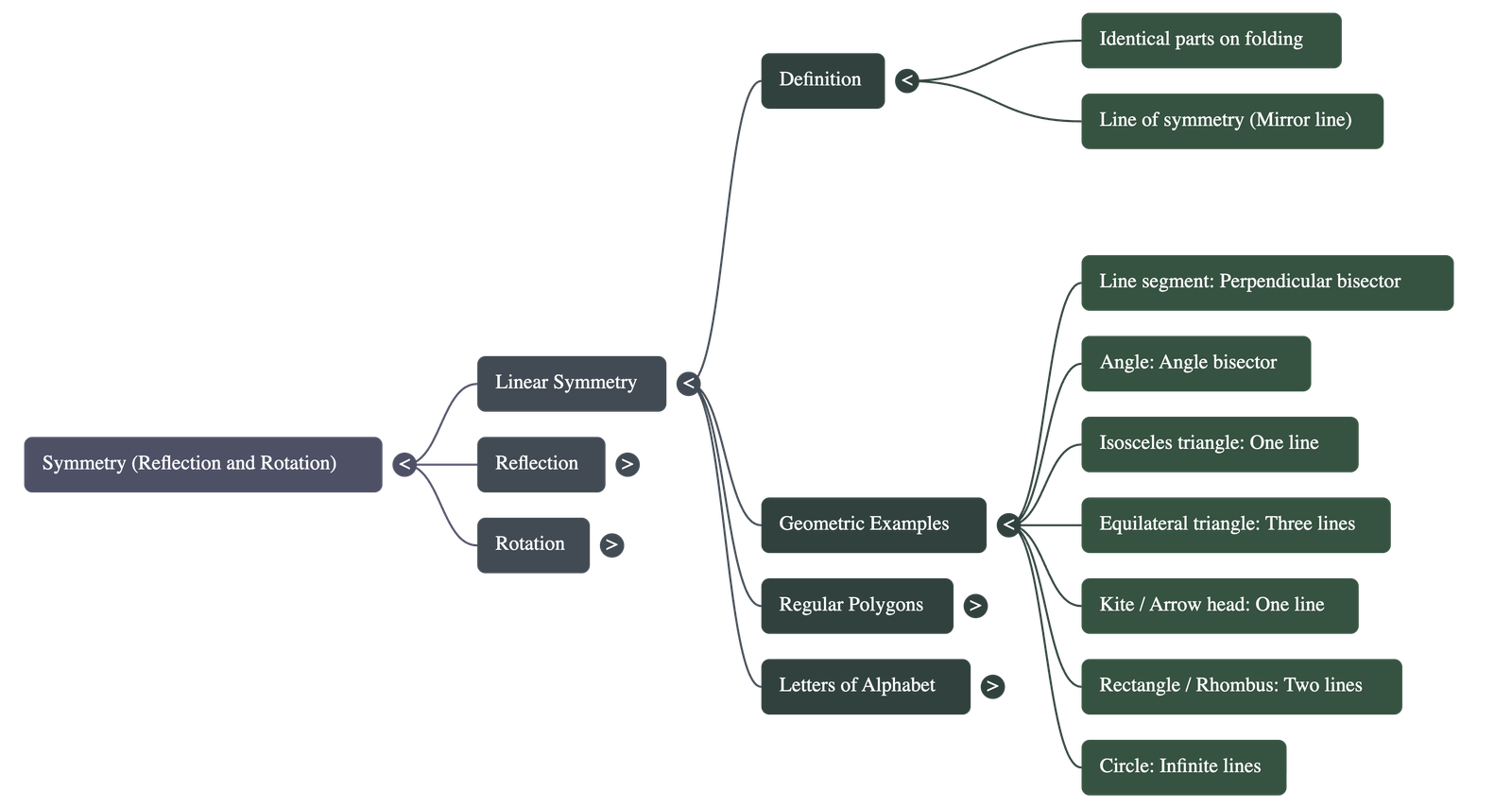
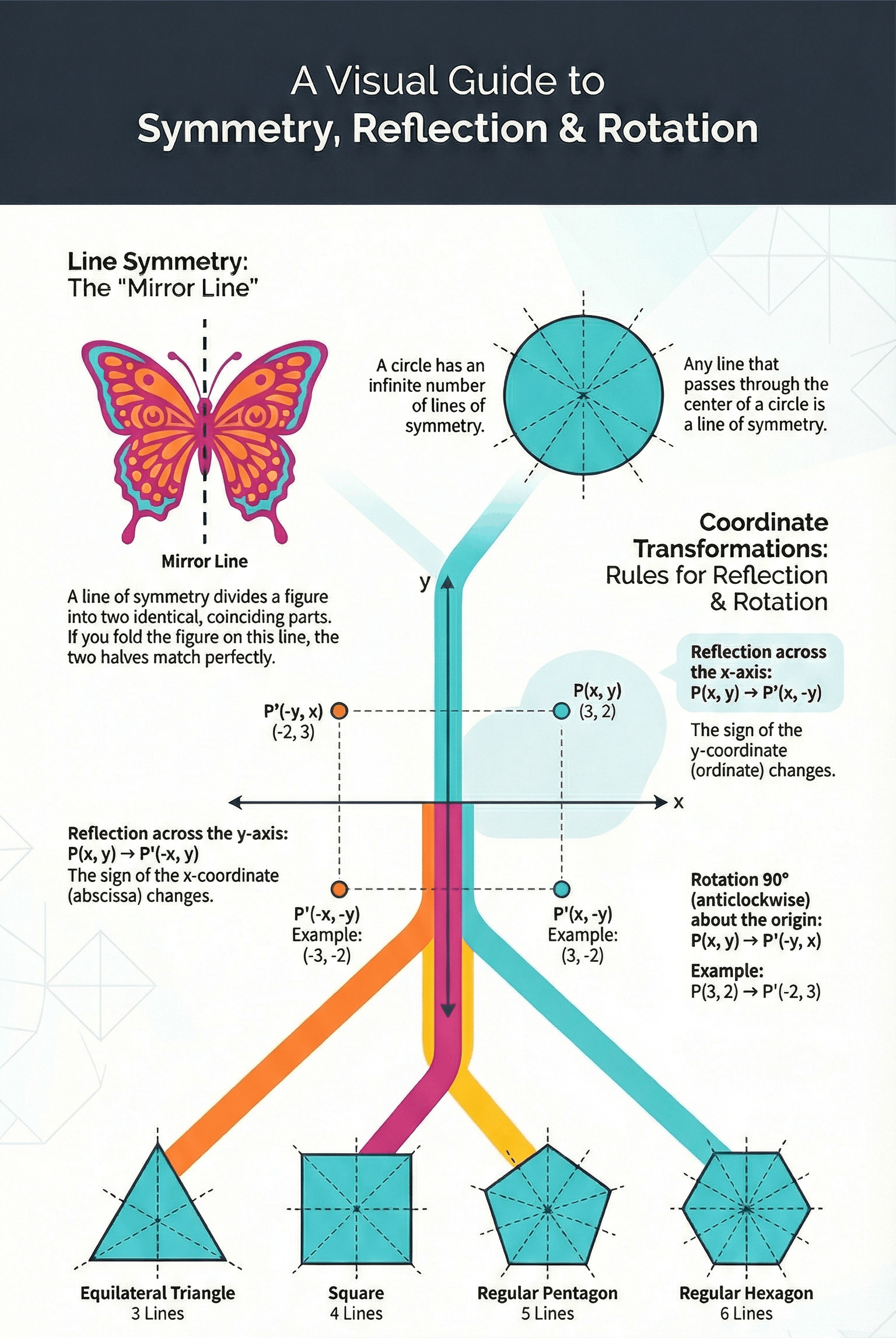
• Definition: A plane figure possesses linear symmetry if it can be folded along a line so that the two parts exactly coincide.
• Line of Symmetry: The fold line where the figure is symmetrical is called the line of symmetry, axis of symmetry, or mirror line.
• Line Segment: A line segment is symmetrical about its perpendicular bisector.
• Angles: An angle with equal arms is symmetrical about its angle bisector.

2. Symmetry in Geometric Shapes

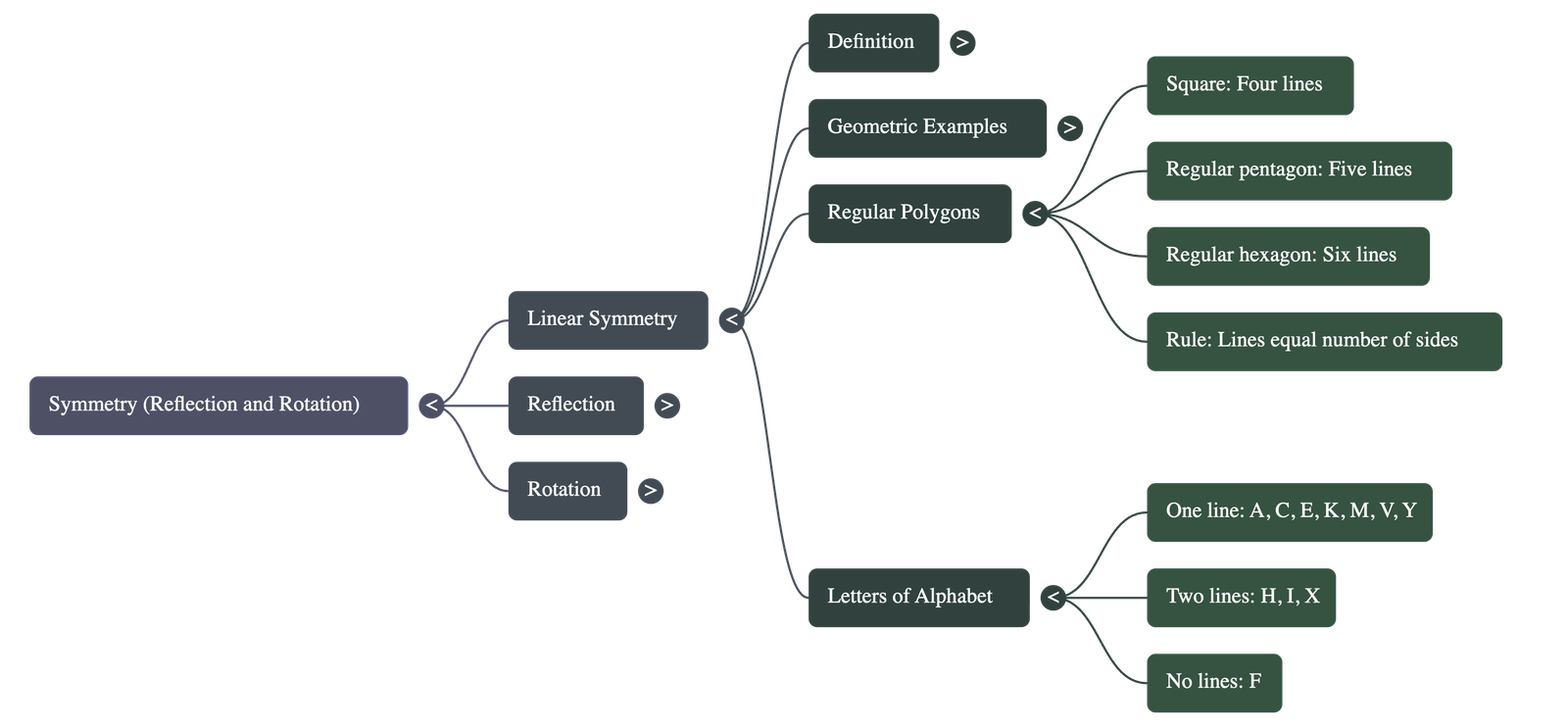
• Triangles: An isosceles triangle has one line of symmetry (the vertex angle bisector), while an equilateral triangle has three (the bisectors of each angle).
• Quadrilaterals: Kites and arrowheads have one line of symmetry. Rectangles and rhombuses each have two.
• Regular Polygons: In any regular polygon, the number of lines of symmetry is equal to the number of sides (e.g., a square has 4, a regular pentagon has 5, and a regular hexagon has 6).
• Circles: A circle has an infinite number of lines of symmetry, as any line passing through the centre acts as an axis of symmetry.

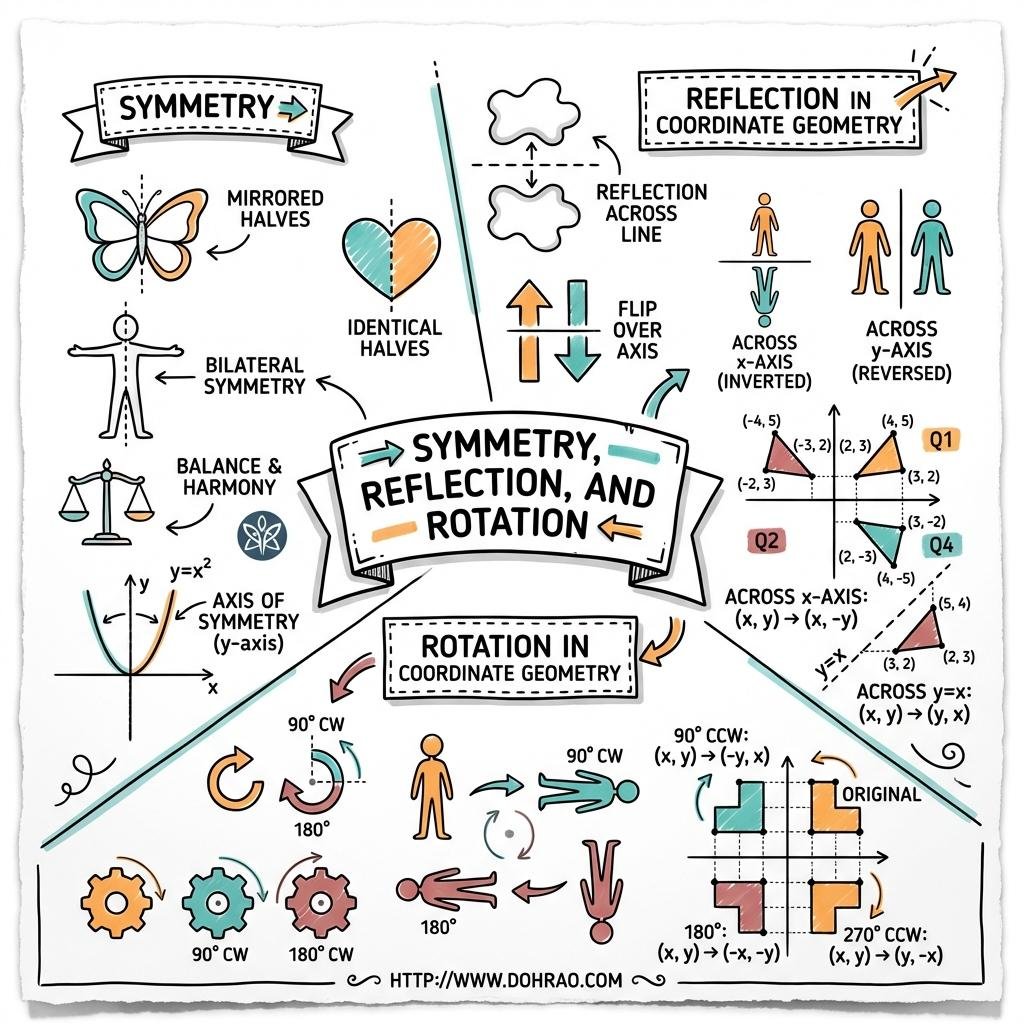
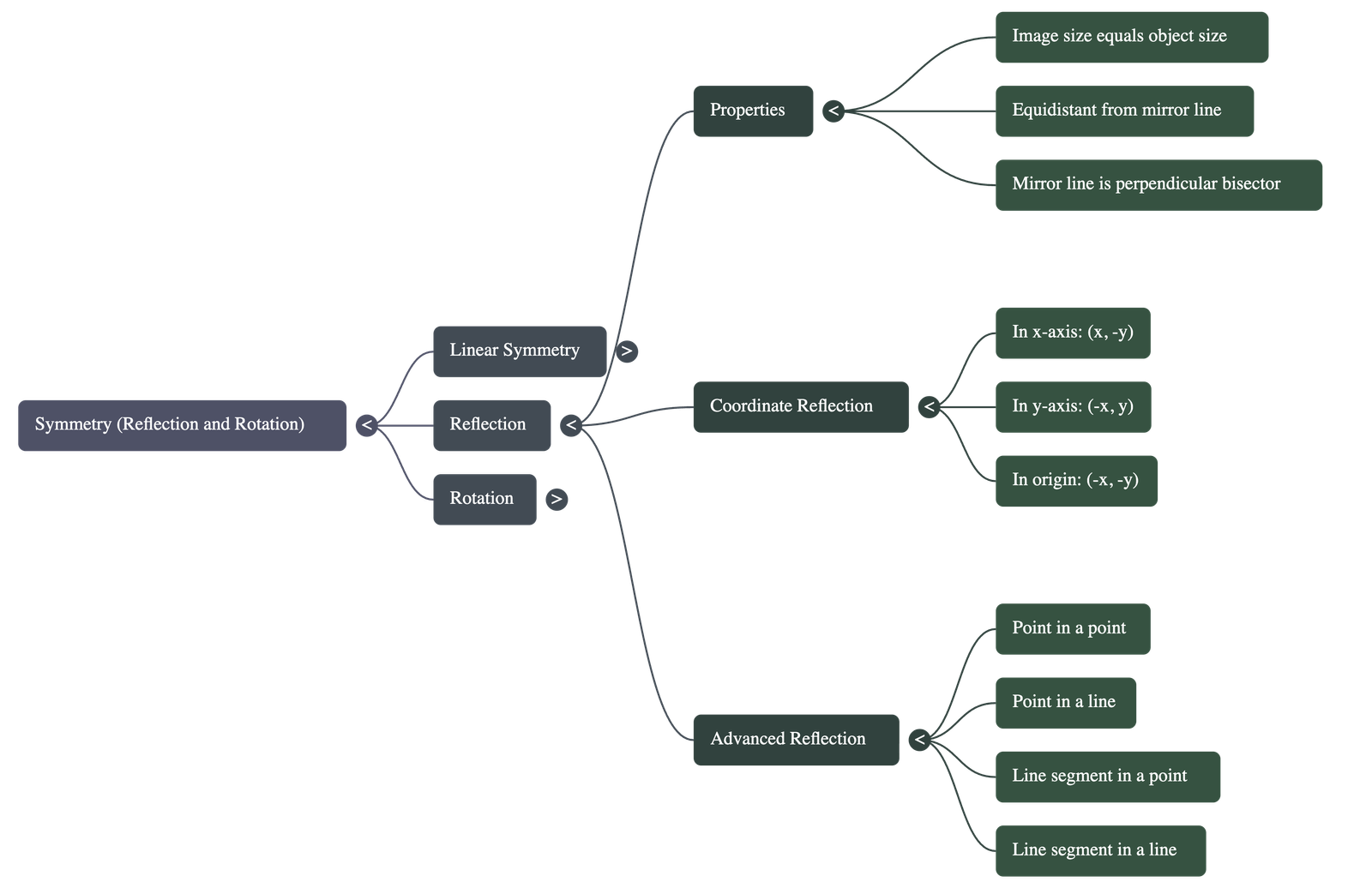
3. Reflection in Co-ordinates

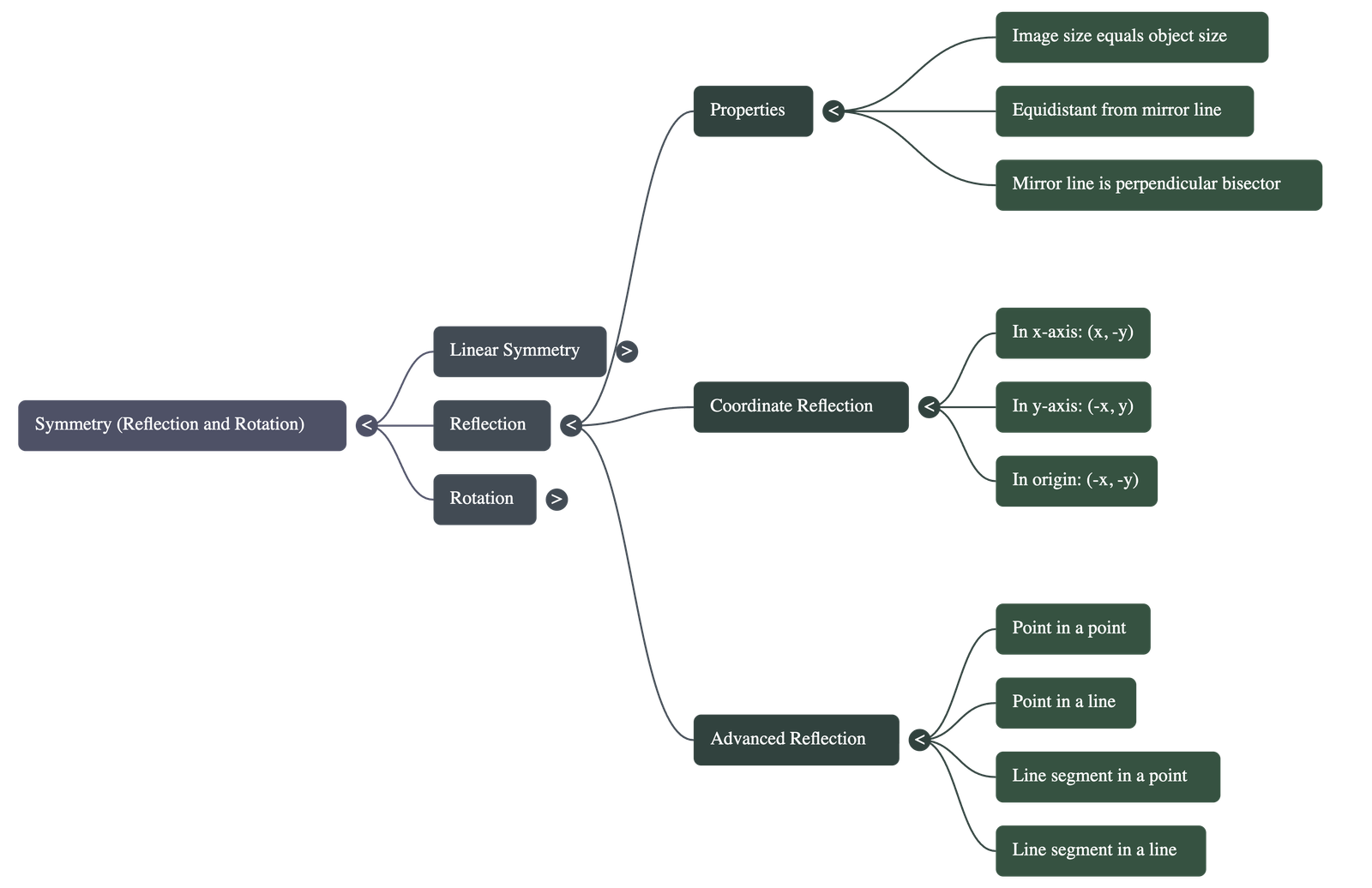
• Reflection in x-axis: When a point (x, y) is reflected in the x-axis, the sign of its y-coordinate changes, resulting in (x, -y).
• Reflection in y-axis: When a point (x, y) is reflected in the y-axis, the sign of its x-coordinate changes, resulting in (-x, y).
• Reflection in Origin: When a point is reflected in the origin, the signs of both the x and y coordinates change, resulting in (-x, -y).
• Properties: The image is the same size as the object, at the same distance behind the mirror line as the object is in front, and the mirror line is the perpendicular bisector of the segment joining the object and its image.

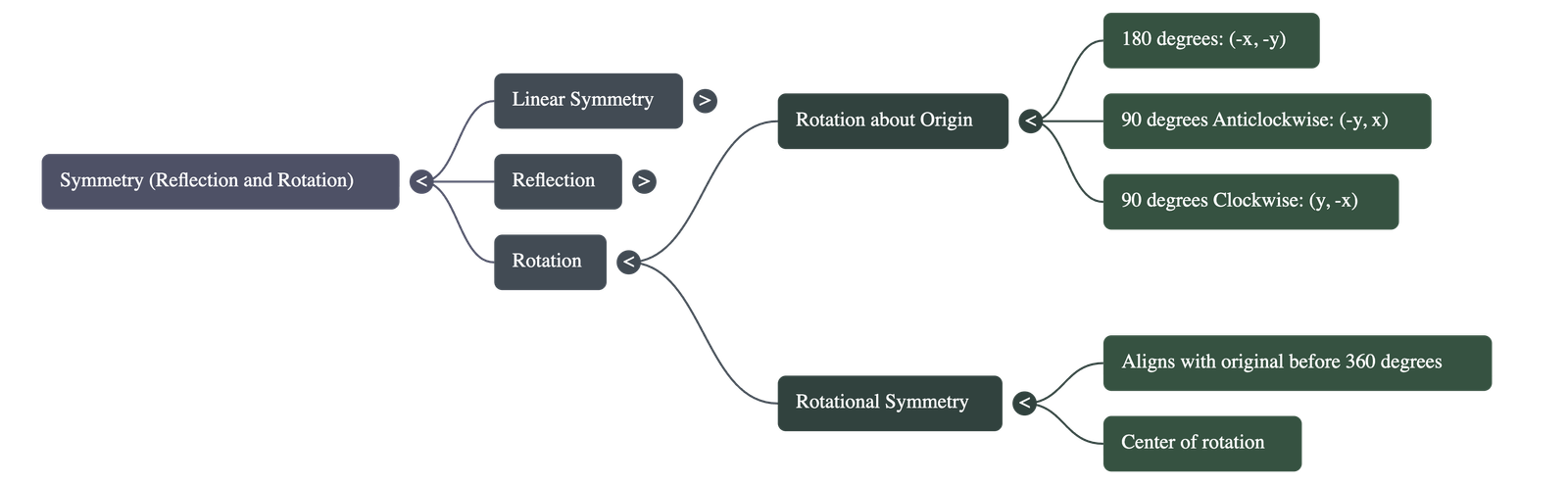
4. Rotation

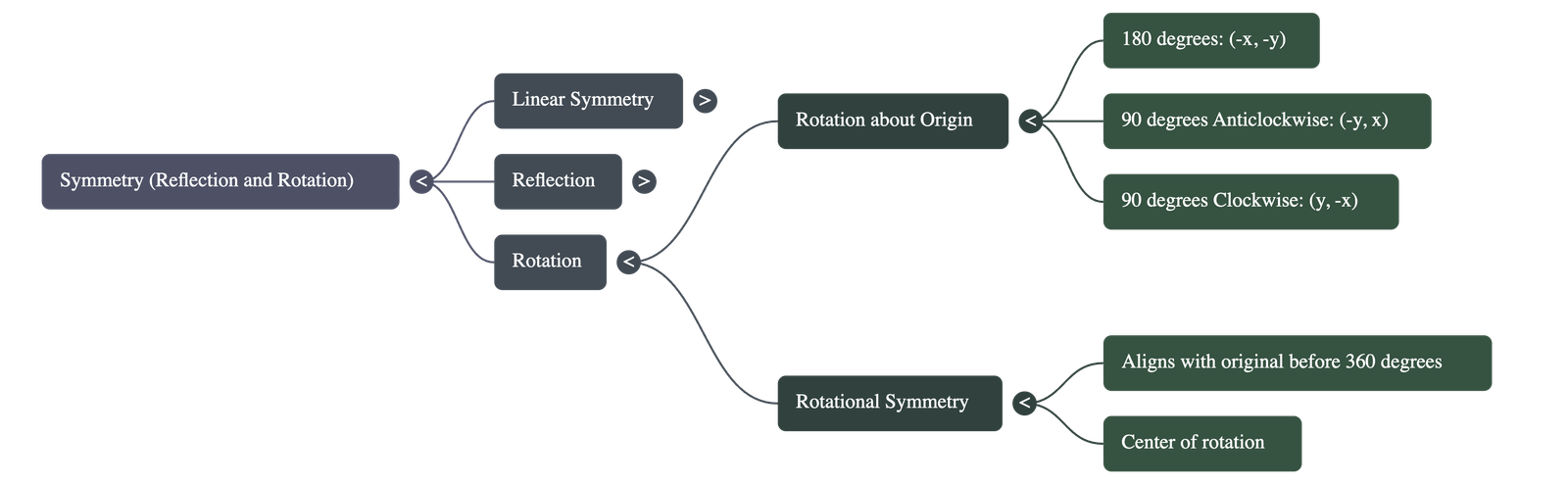
• 180° Rotation: Rotating a point (x, y) through 180° about the origin (clockwise or anticlockwise) results in the point (-x, -y).
• 90° Anticlockwise Rotation: Rotating a point (x, y) 90° anticlockwise about the origin results in (-y, x).
• 90° Clockwise Rotation: Rotating a point (x, y) 90° clockwise about the origin results in (y, -x).

5. Geometric Reflections

• Point in a Point: To reflect point A in point P, produce a segment AP to A' such that AP = PA'.
• Point in a Line: To reflect point P in line AB, draw a perpendicular PO to the line and extend it to P' so that PO = OP'.
• Line Segments: The reflection of a line segment (either in a point or a line) results in an image segment of the same length.