Chapter 19 Summary: Representing 3-D in 2-D

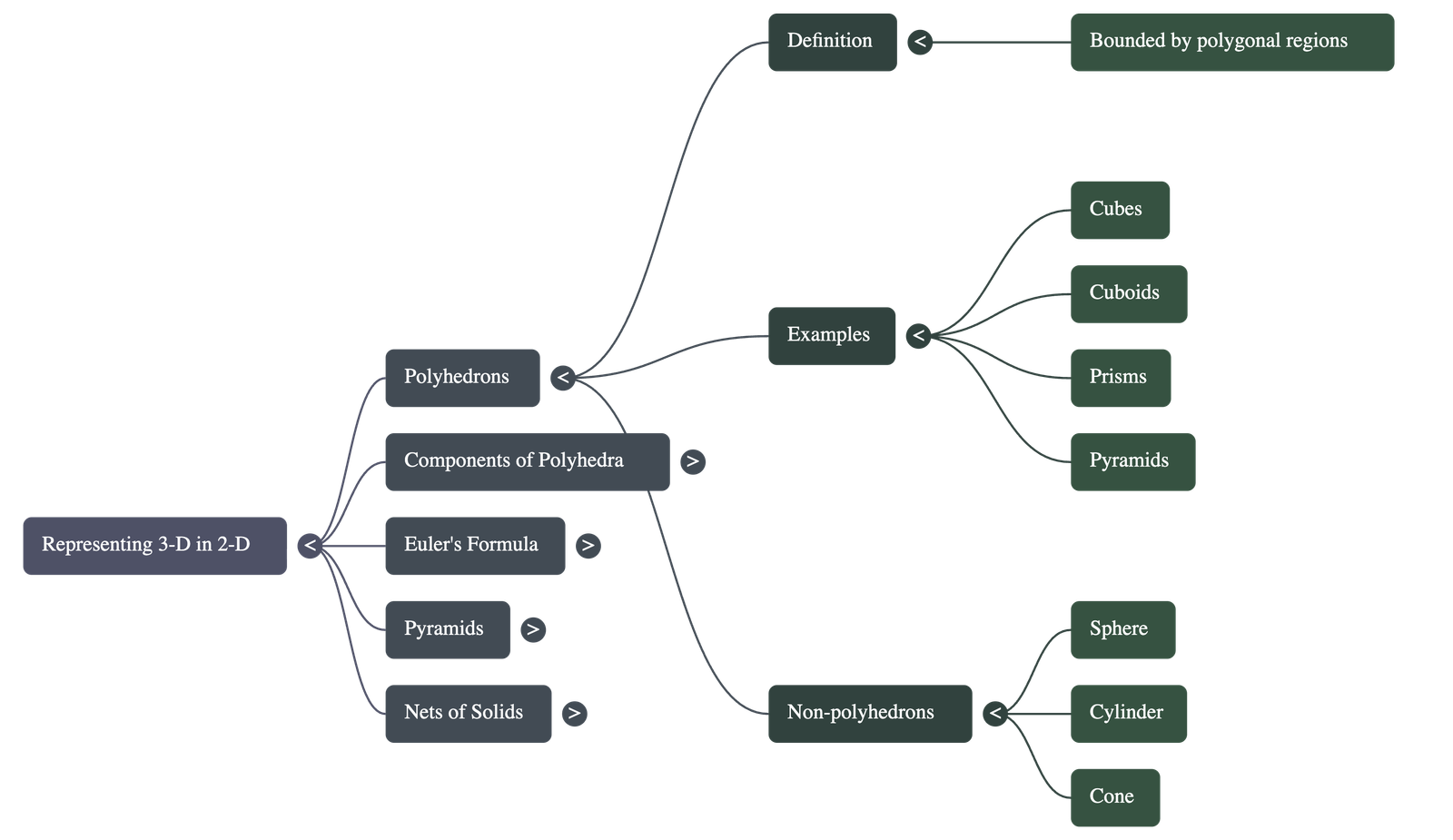
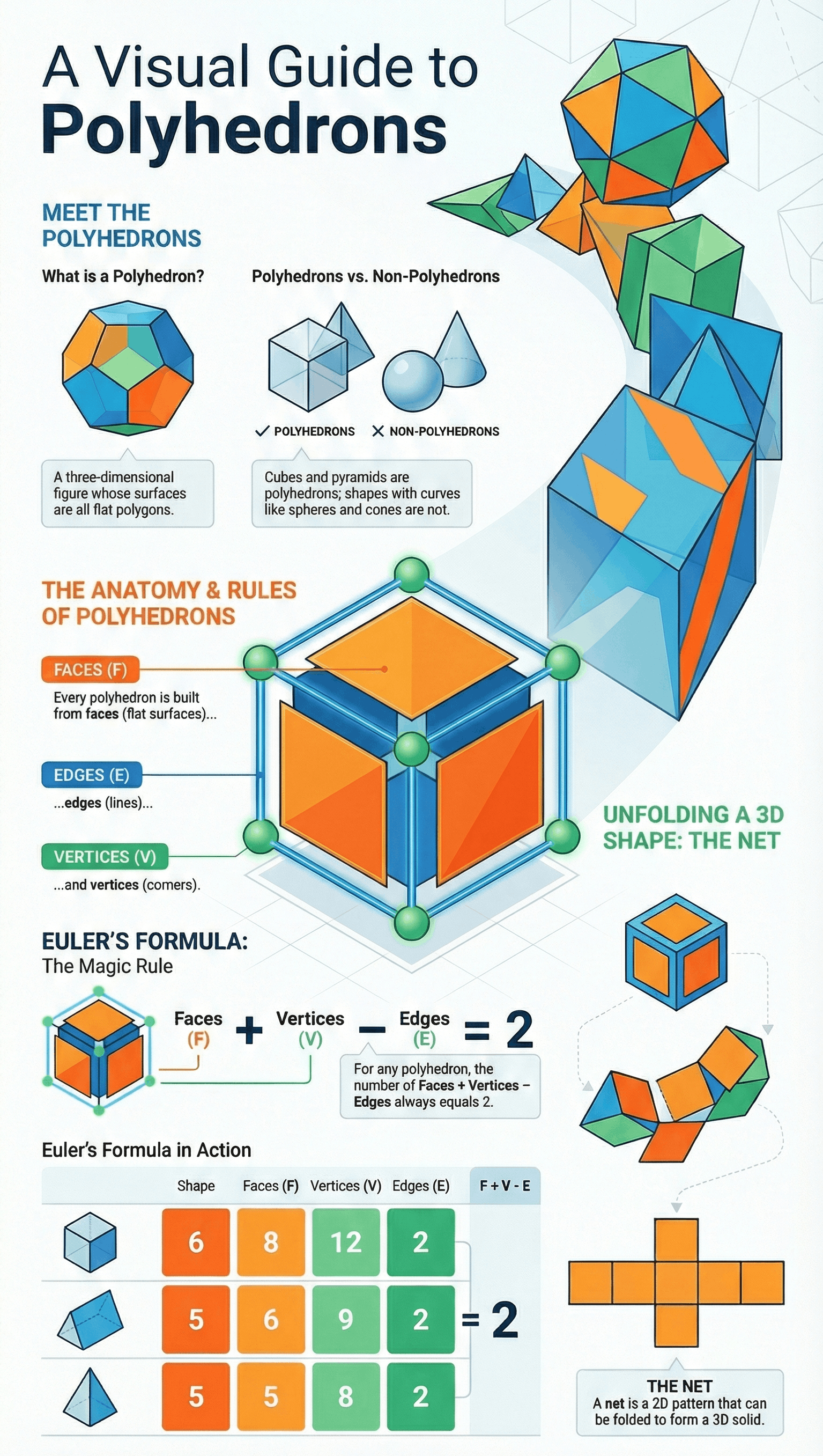
1. Introduction to Polyhedrons

• Core Concept: This chapter focuses on visualizing 3D objects as 2D representations and cross-sections.
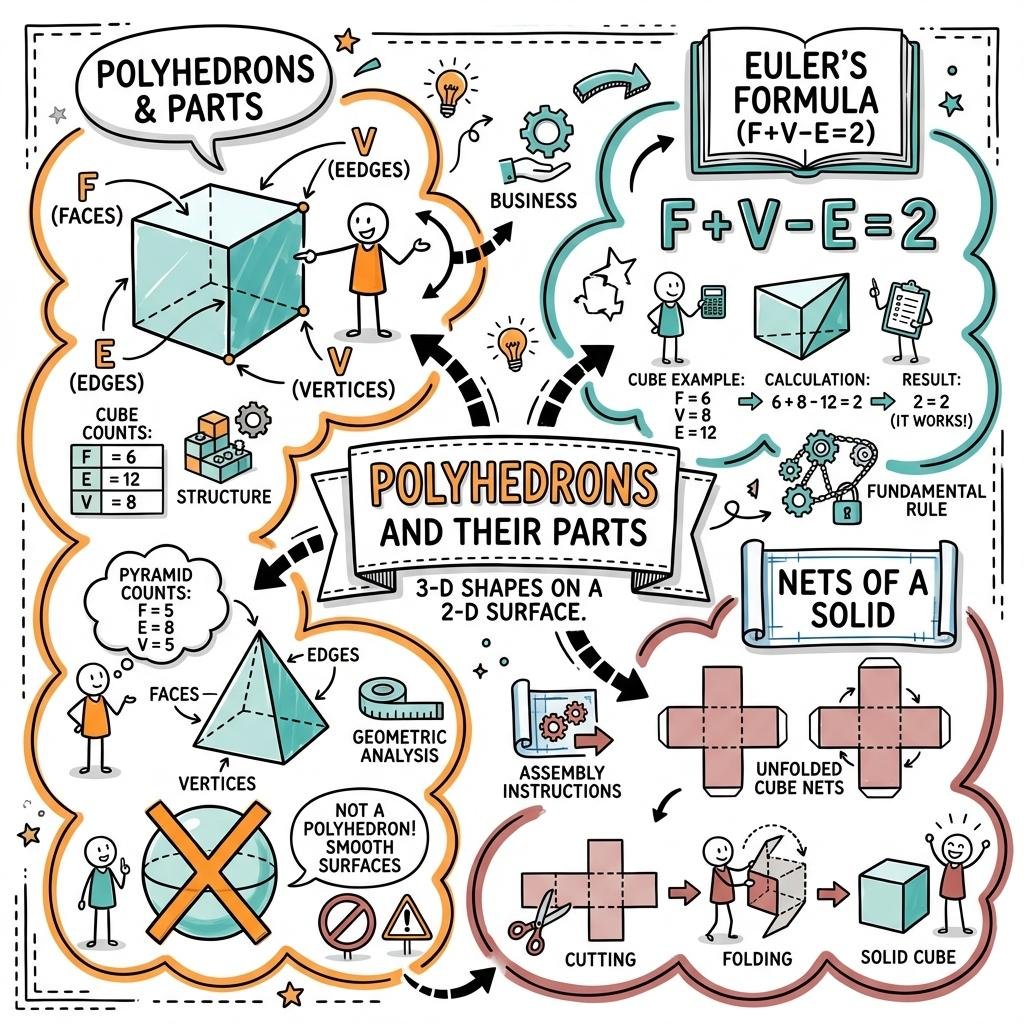
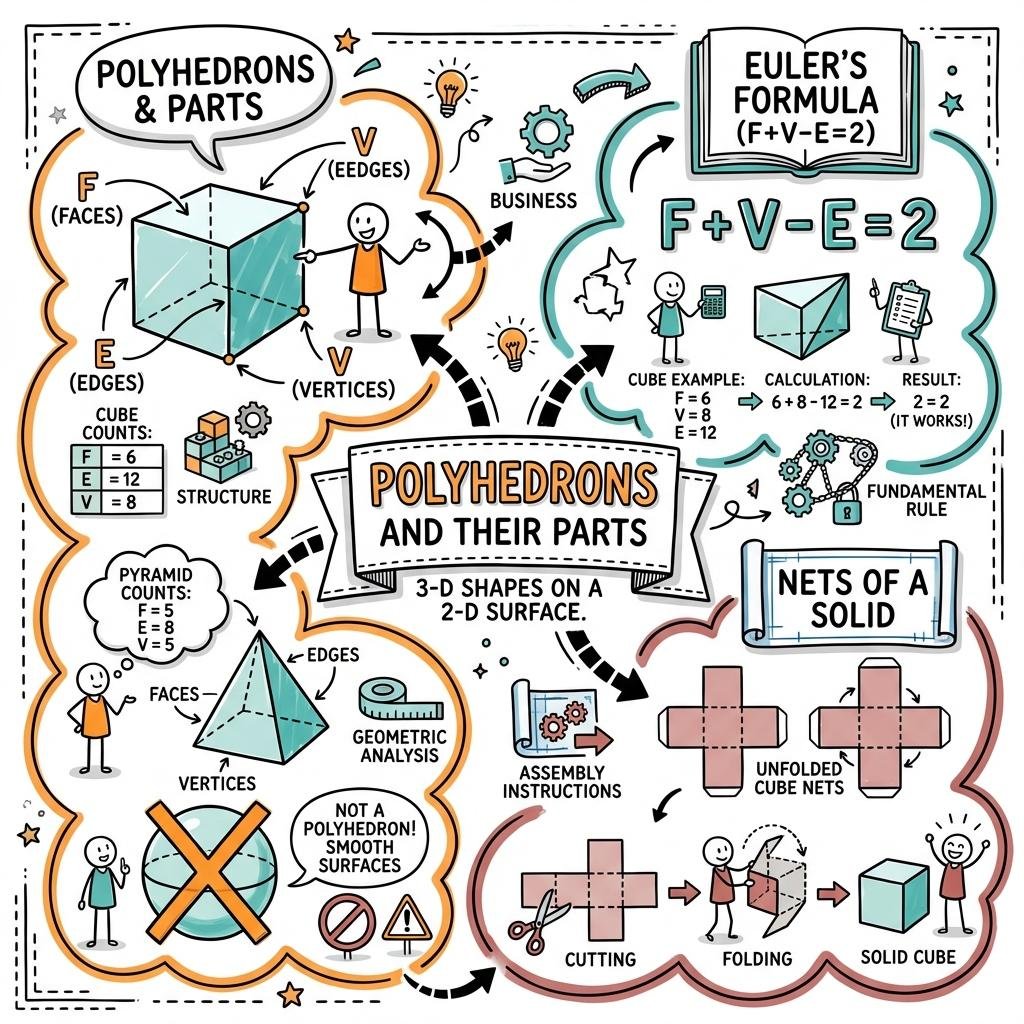
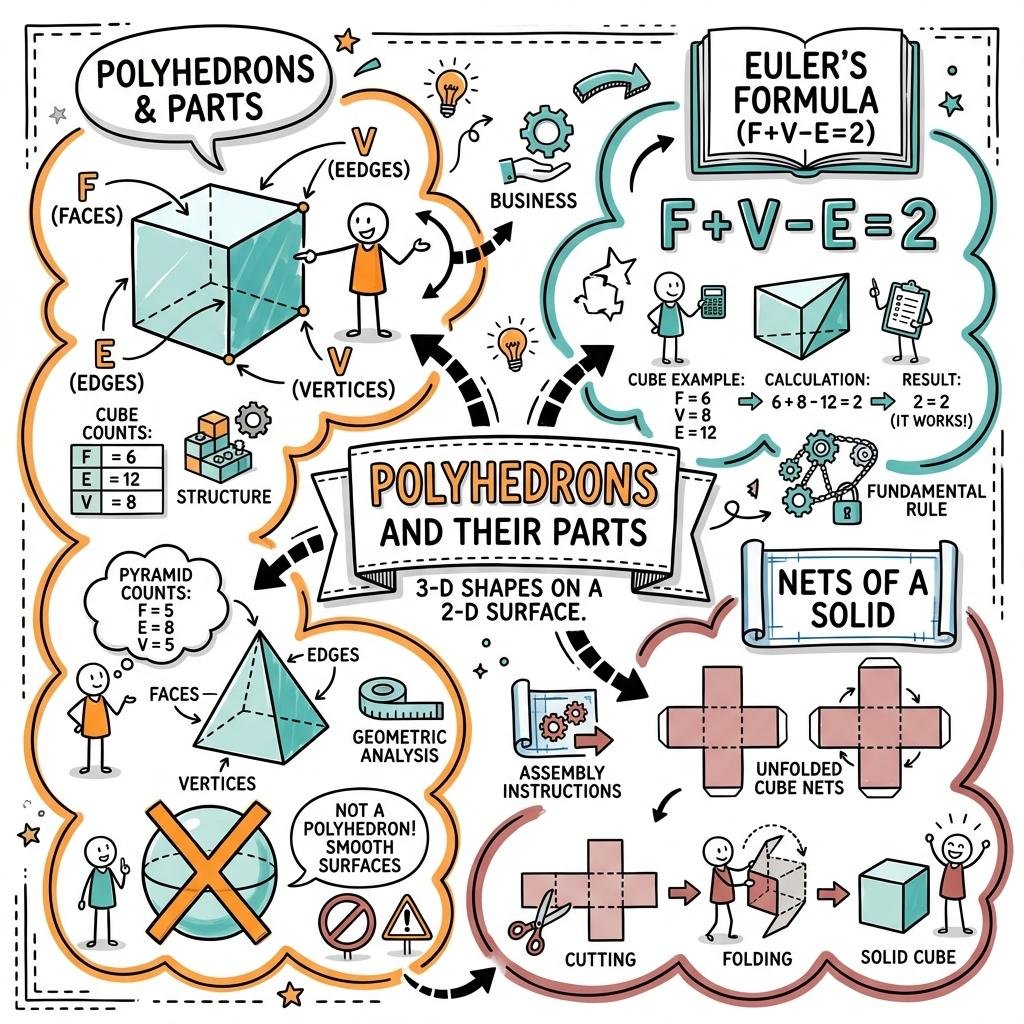
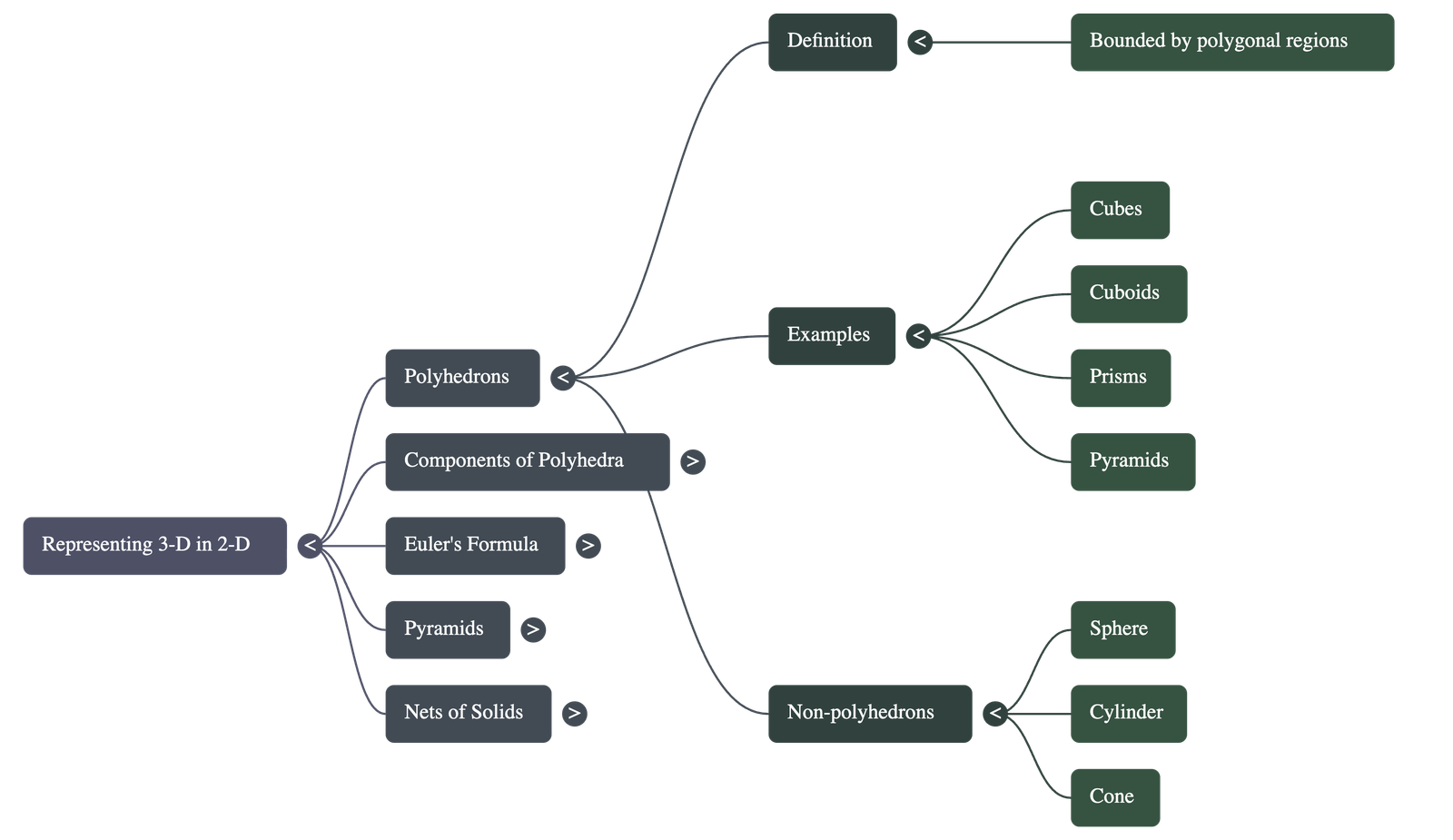
• Definition: A polyhedron is a three-dimensional figure bounded by polygonal regions (faces).
• Classifications:
  • Polyhedrons: Cubes, cuboids, prisms, and pyramids (all have flat polygonal faces).
  • Non-Polyhedrons: Spheres, cylinders, and cones (these include curved surfaces).

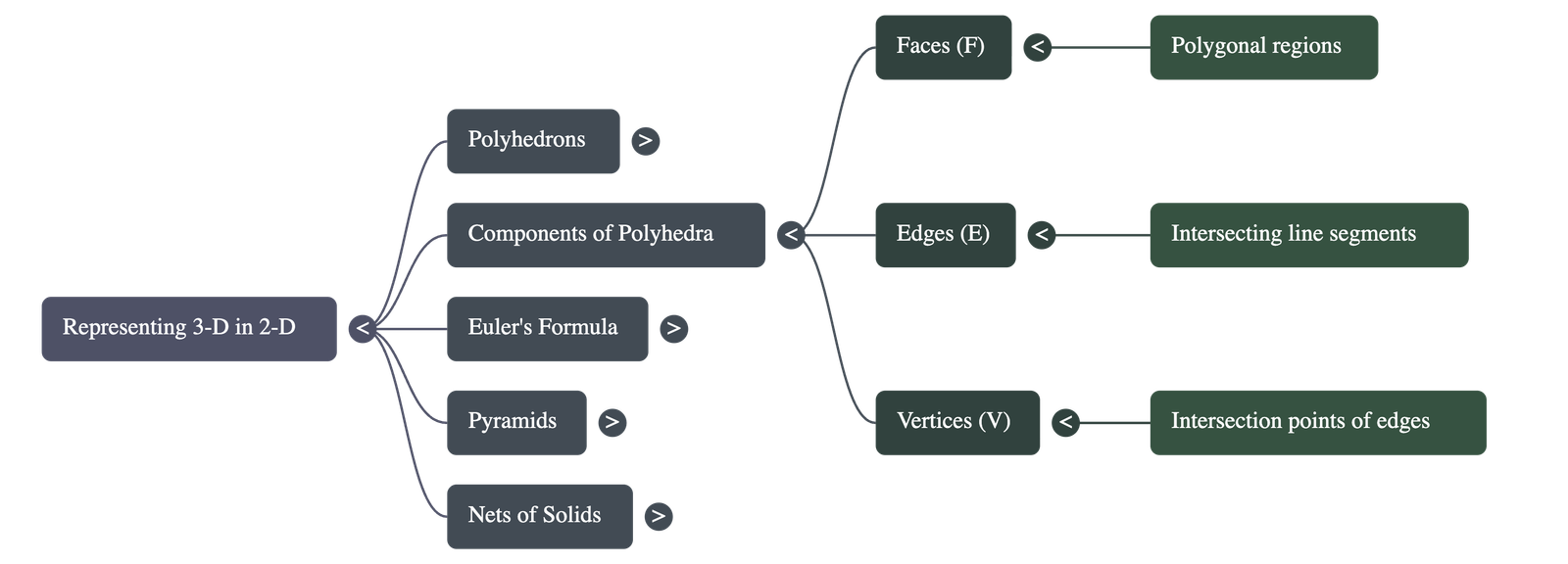
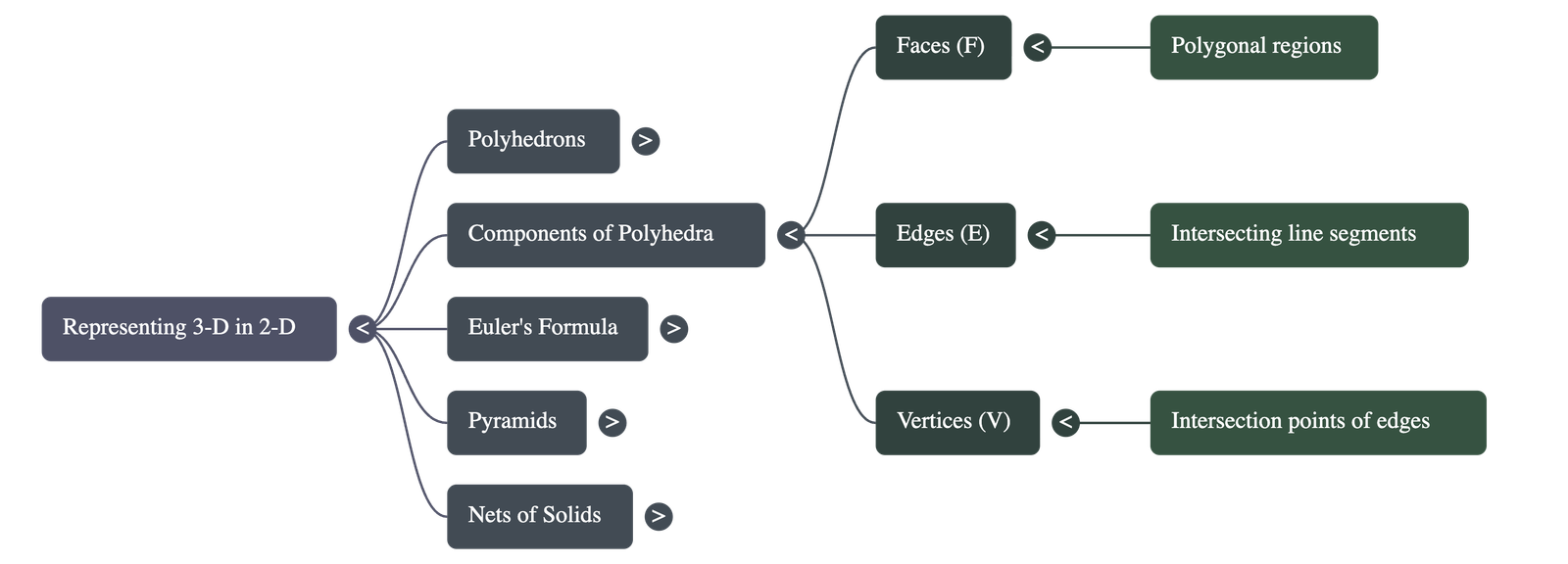
2. Key Components of Polyhedra

Every polyhedron is defined by three primary elements:

• Faces (F): The flat polygonal regions that form the surface of the solid.
• Edges (E): The line segments where two faces intersect.
• Vertices (V): The points where edges meet (corners).

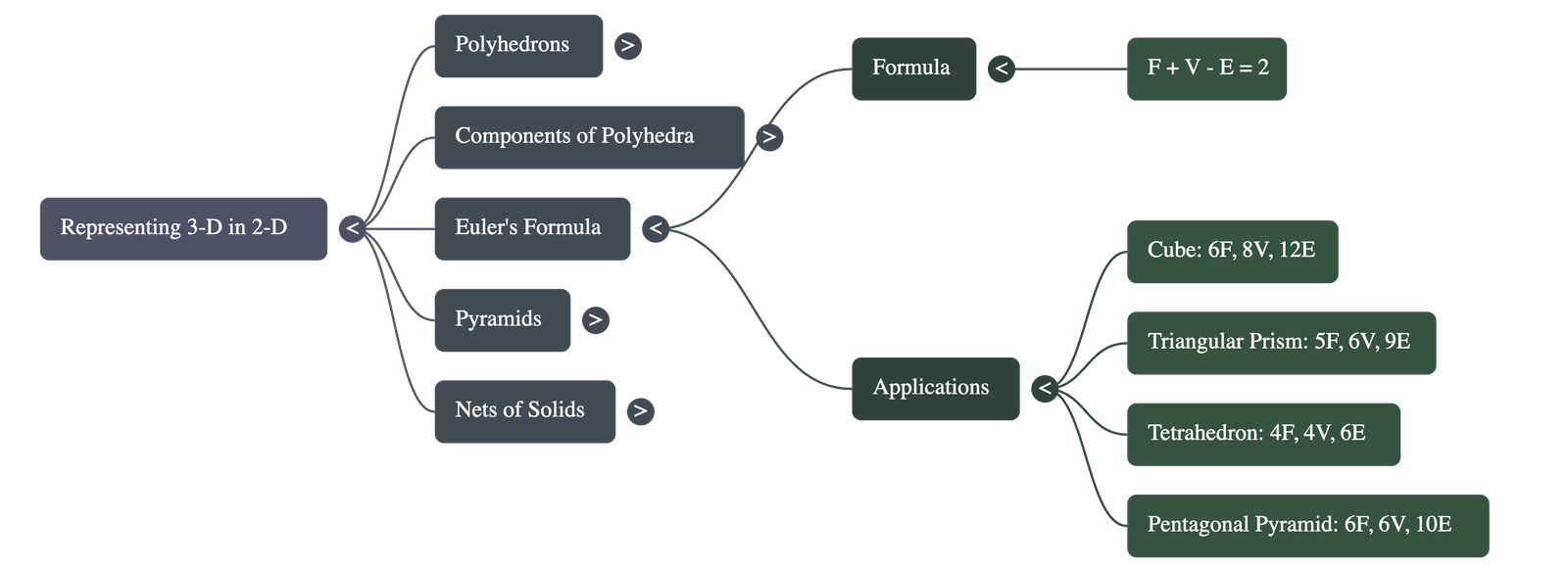
3. Euler’s Formula

A fundamental mathematical relationship exists for all polyhedra, known as Euler's Formula:

This formula allows for the calculation of an unknown number of faces, vertices, or edges if the other two are known.

4. Types of Prisms and Pyramids

• Prisms: Solids with congruent and parallel polygonal bases (ends) and side faces that are parallelograms. Examples include triangular, pentagonal, and hexagonal prisms.
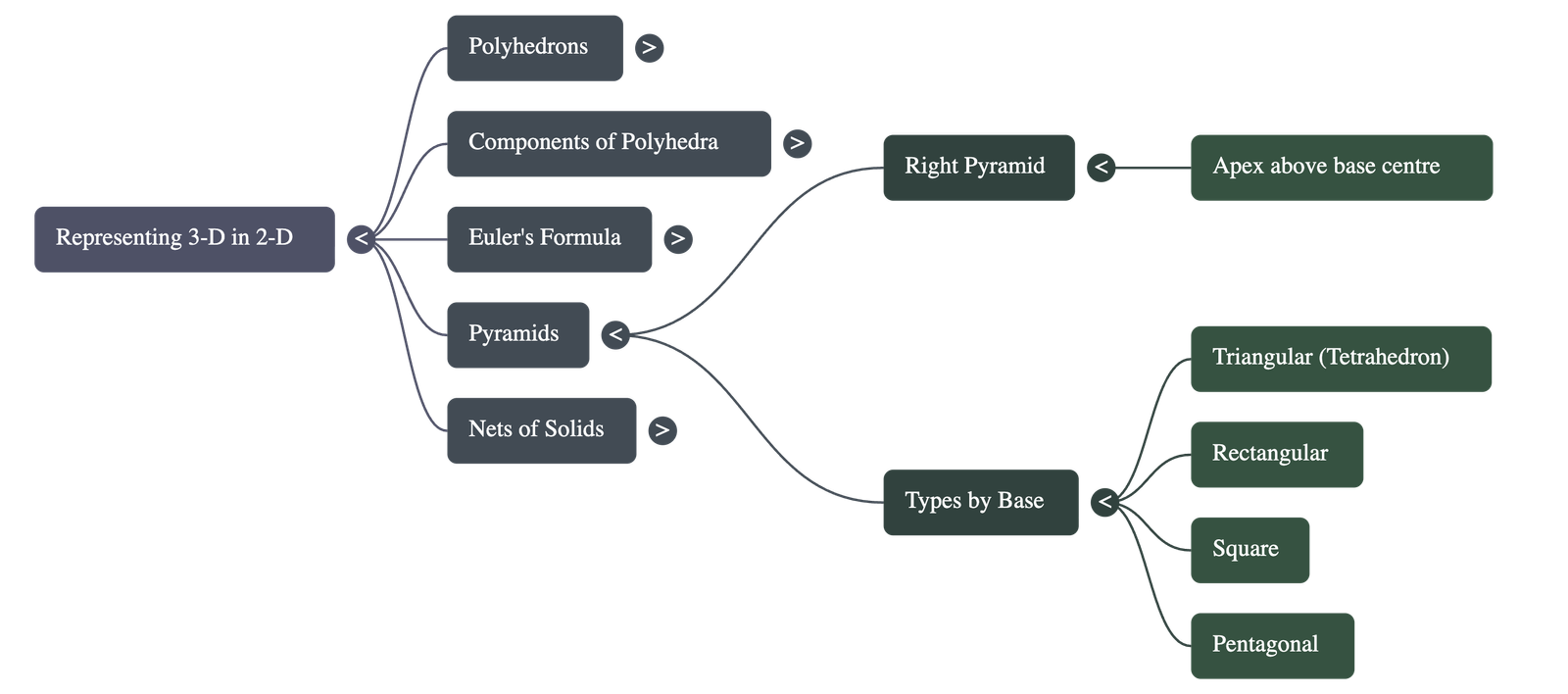
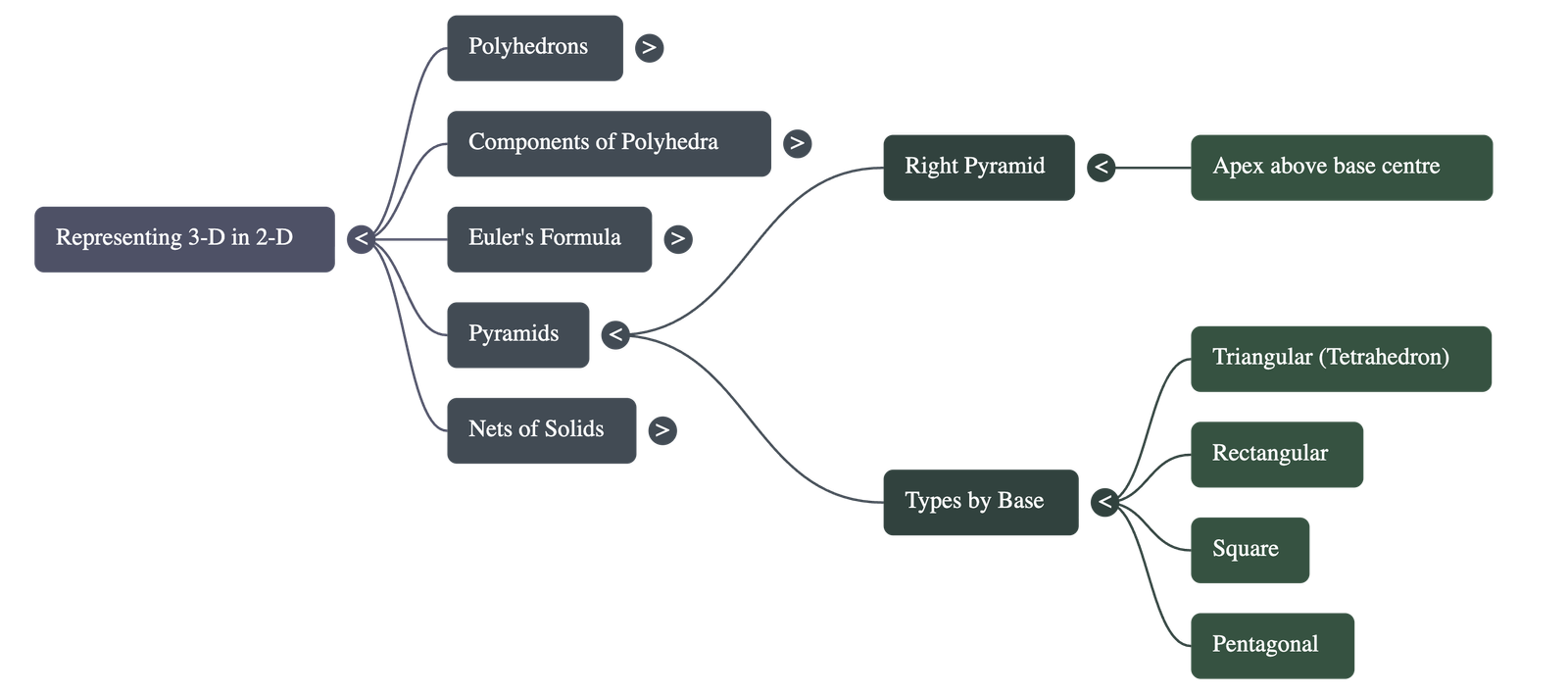
• Pyramids: Solids with a polygonal base and triangular lateral faces that meet at a single point called the apex.
  • A right pyramid has its apex directly above the centre of the base.
  • A tetrahedron is a triangular pyramid with four faces.

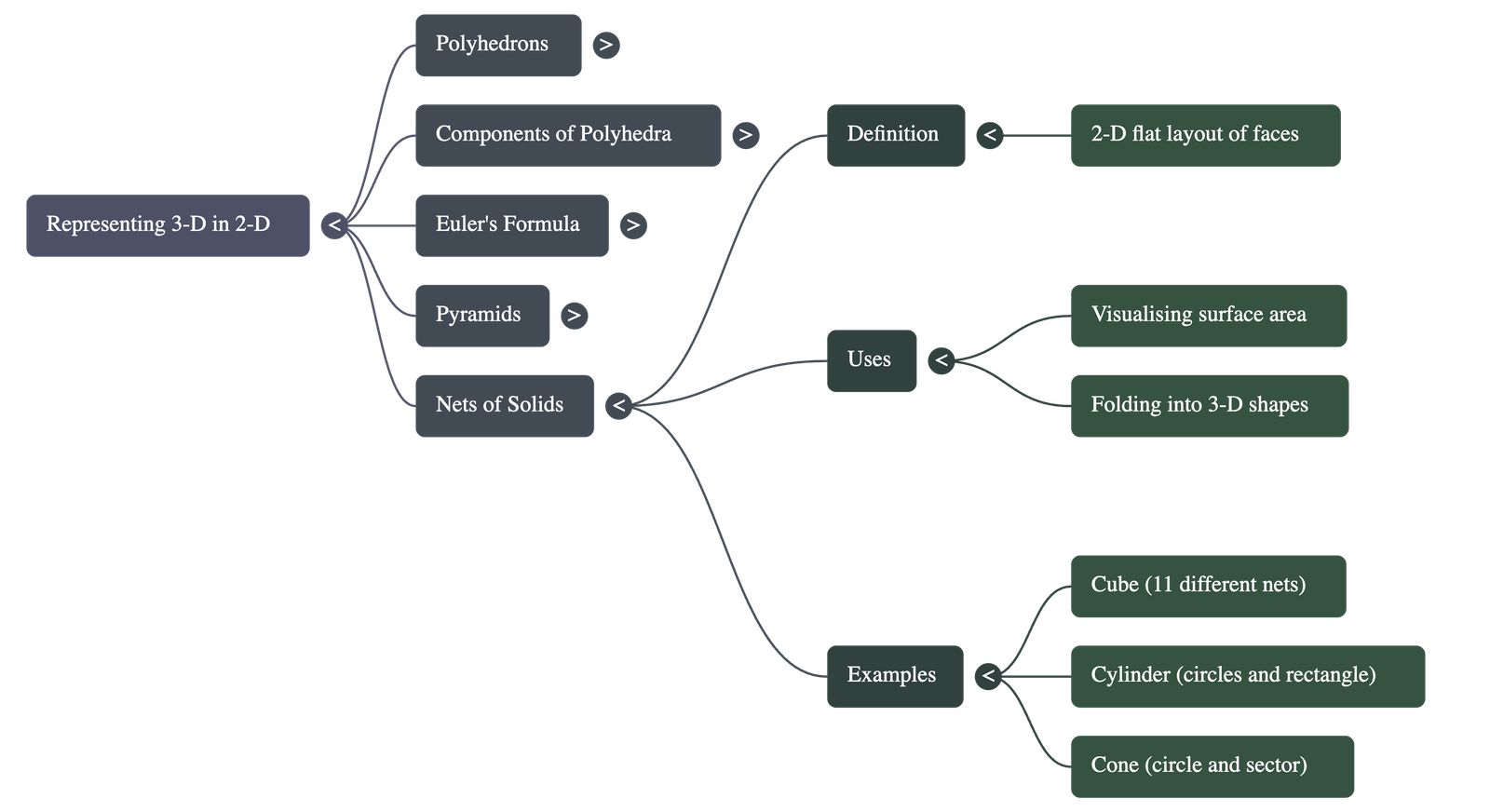
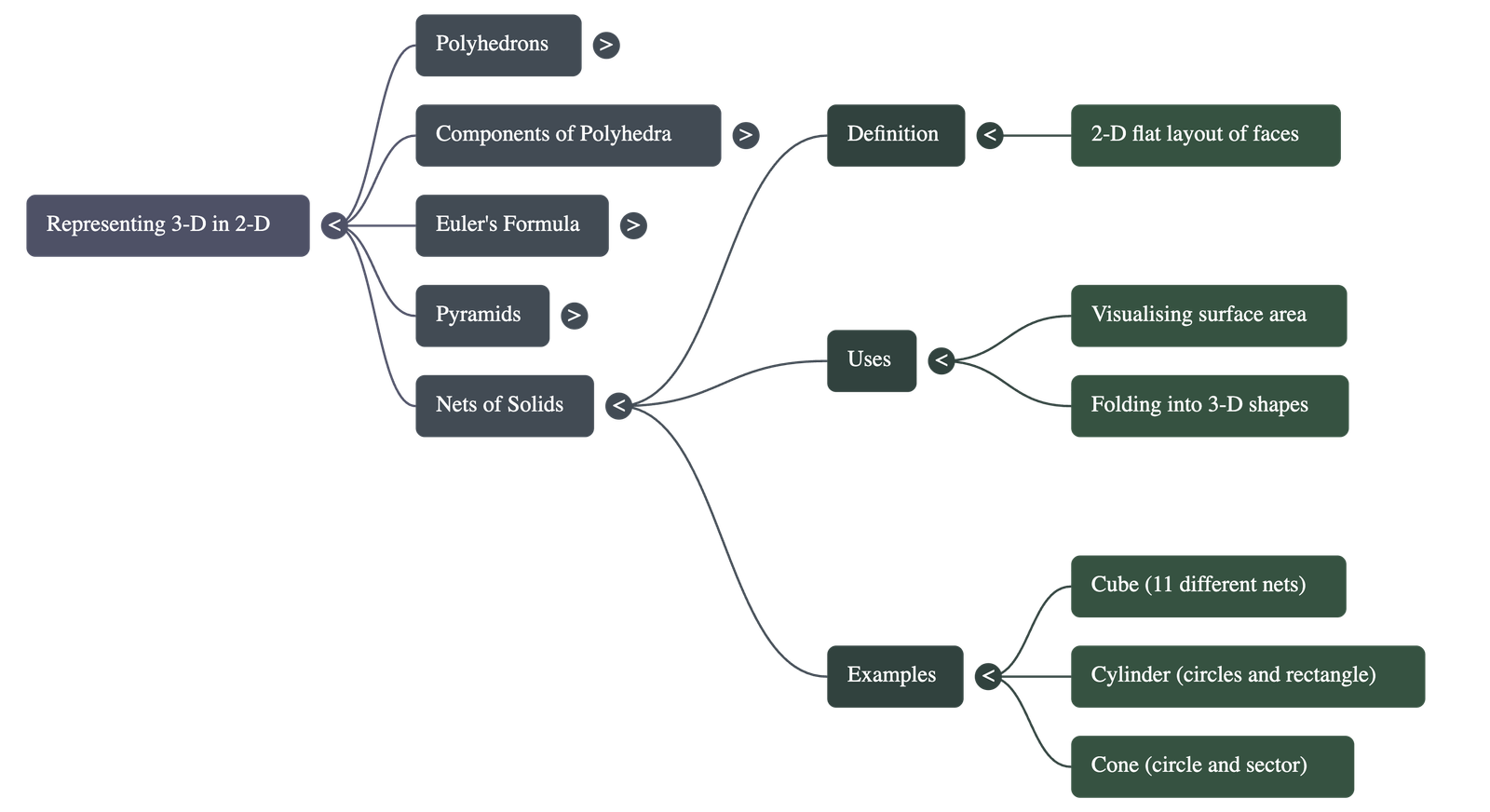
5. Nets of Solids

• Definition: A net is a 2D pattern made by laying out the surface of a 3D figure flat. When folded, it forms the 3D solid.
• Cube Nets: A cube is unique in that it can be represented by 11 different nets.
• Utility: Nets are highly useful for visualizing the structure of a solid and for calculating its total surface area.
• Examples: The chapter illustrates nets for various shapes including cylinders, cones, and diverse pyramids.