Summary of Chapter 4: Cubes and Cube-Roots

1. Fundamentals of Cubes

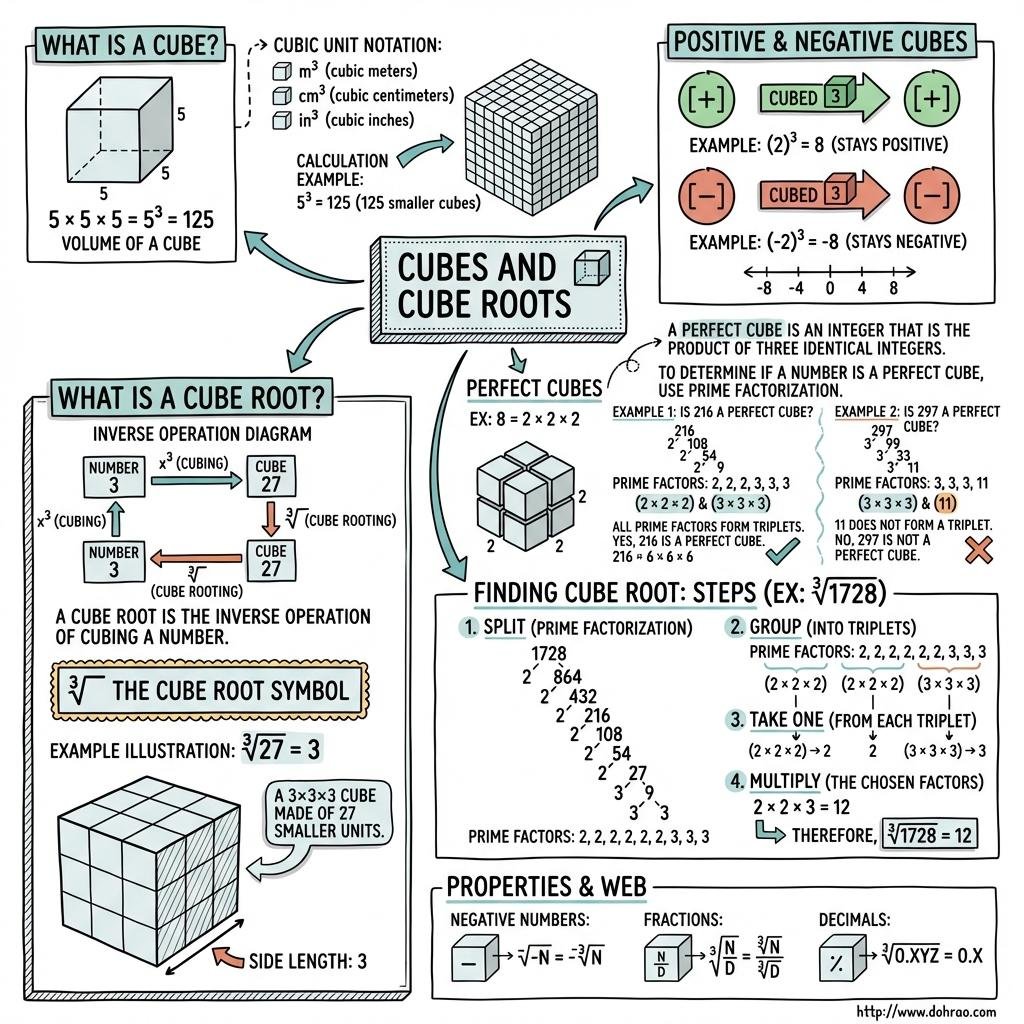
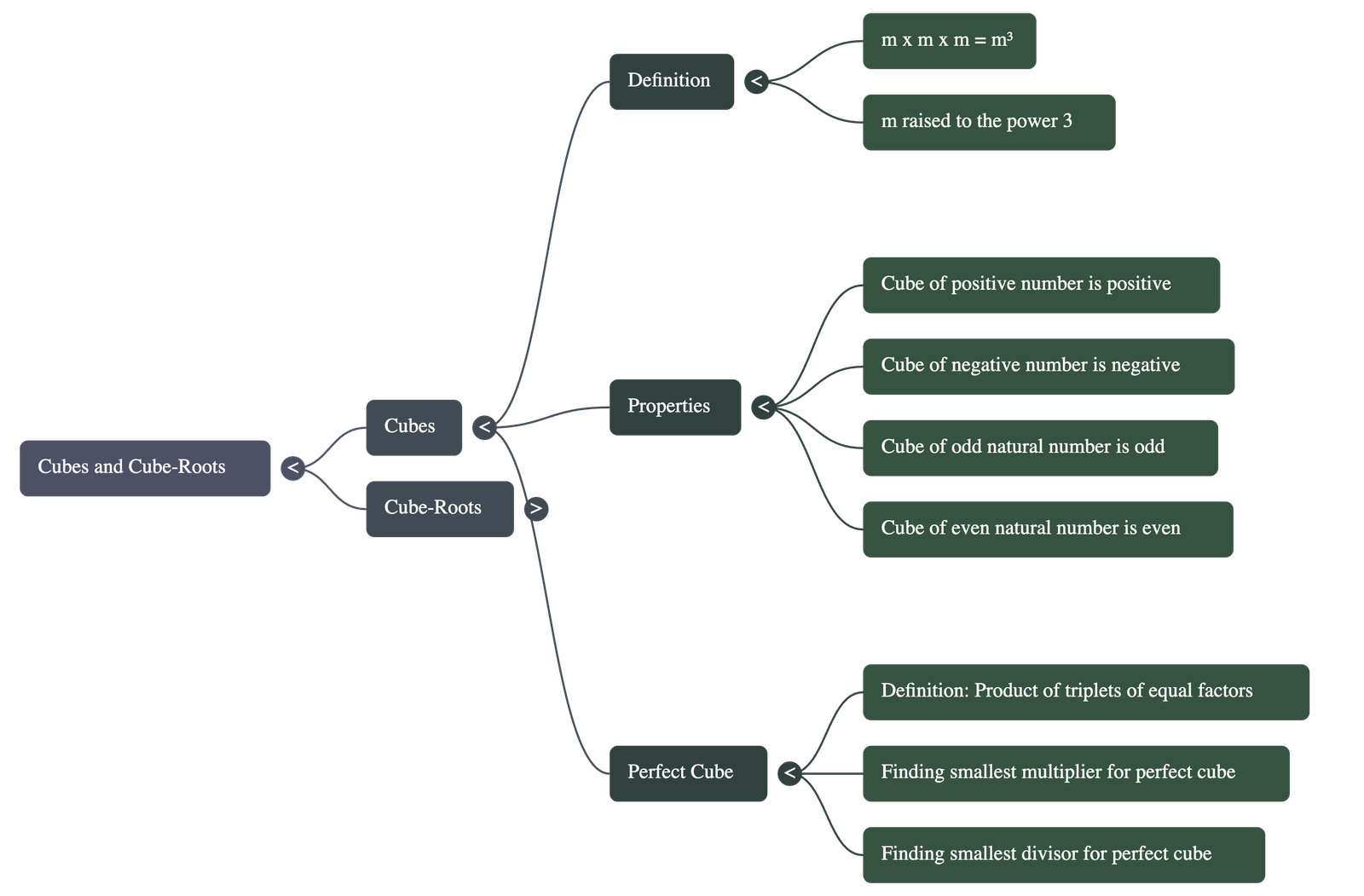
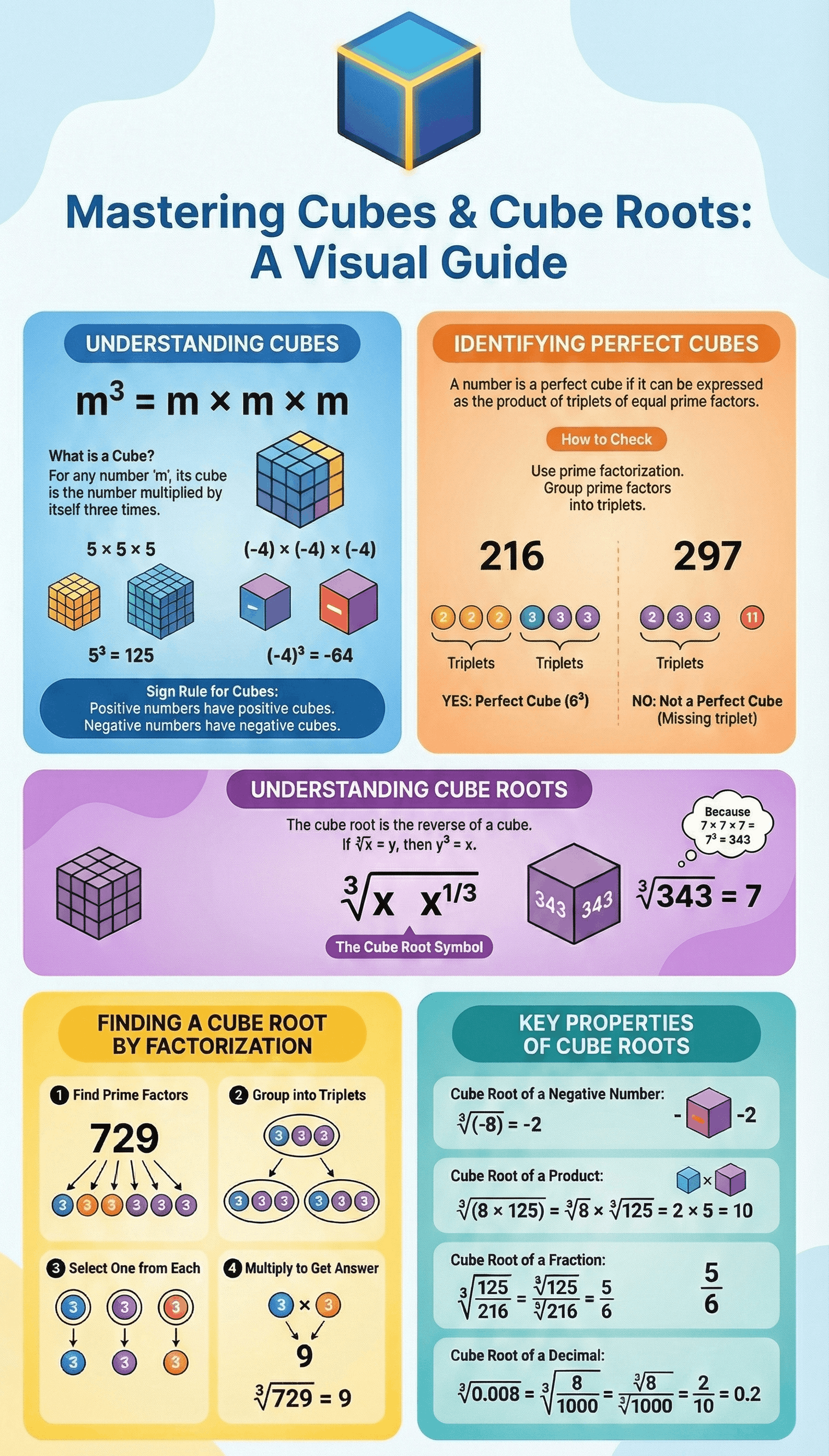
• Definition: For any number m, the product obtained by multiplying the number by itself three times (m × m × m) is called the cube of m, written as m³.
• Perfect Cubes: A natural number is a perfect cube if it can be expressed as the product of triplets of equal prime factors. For instance, 216 is a perfect cube because it factors into (2 × 2 × 2) × (3 × 3 × 3).
• Parity of Cubes: The cubes of even natural numbers are always even (e.g., 8³ = 512), and the cubes of odd natural numbers are always odd (e.g., 5³ = 125).
• Signs of Cubes: The cube of a positive number is positive, while the cube of a negative number is always negative.

2. Transforming Numbers into Perfect Cubes

• Prime Factorization Method: To determine if a number is a perfect cube, you must find its prime factors. If any factor does not appear in a group of three (a triplet), the number is not a perfect cube.
• Adjusting Numbers: If a number is not a perfect cube, you can find the smallest number to multiply or divide it by to make it one. This is done by identifying which prime factors are missing from a triplet (to multiply) or which factors are extra (to divide).

3. Understanding Cube-Roots

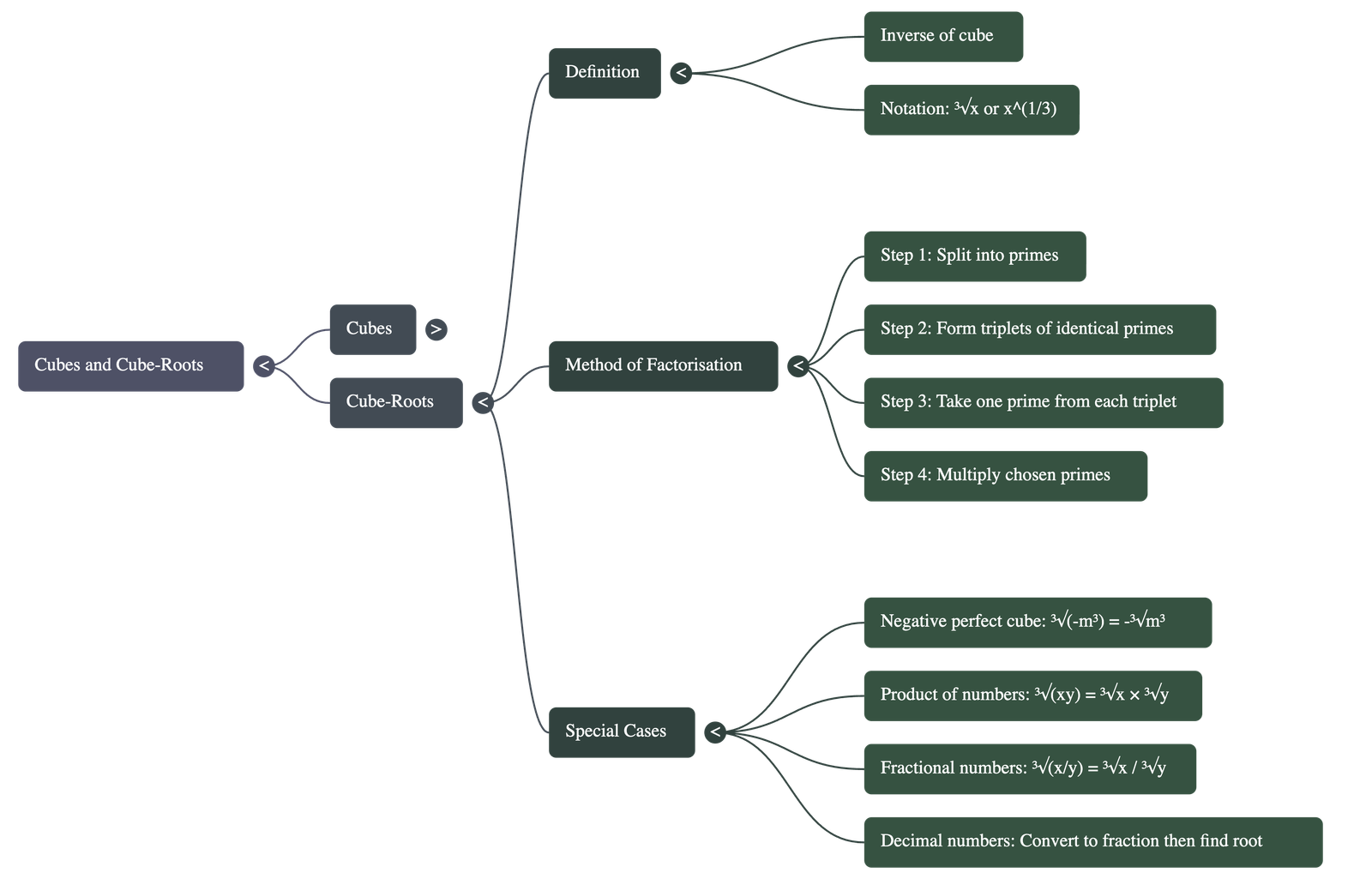
• Mathematical Definition: The cube-root of a number x is the value y such that y³ = x. This is denoted by the symbol ³√x or x^1/3.
• The Factorization Process: To find a cube-root manually:
  1. Resolve the number into its prime factors.
  2. Group these identical primes into triplets.
  3. Take one factor from each triplet.
  4. Multiply these factors together to find the cube-root.

4. Specific Rules for Cube-Roots

• Negative Perfect Cubes: The cube-root of a negative perfect cube is simply the negative of the cube-root of its absolute value. For example, ³√(-8) = -2.
• Product Rule: The cube-root of a product of numbers is equal to the product of their individual cube-roots: ³√(xy) = ³√x × ³√y.
• Fraction Rule: The cube-root of a fraction is the cube-root of the numerator divided by the cube-root of the denominator: ³√(x/y) = ³√x / ³√y.
• Decimal Rule: To find the cube-root of a decimal number, it is best to convert the decimal into a fraction first (e.g., 0.027 becomes 27/1000) and then calculate the cube-root of both parts.