1. Fundamental Definitions

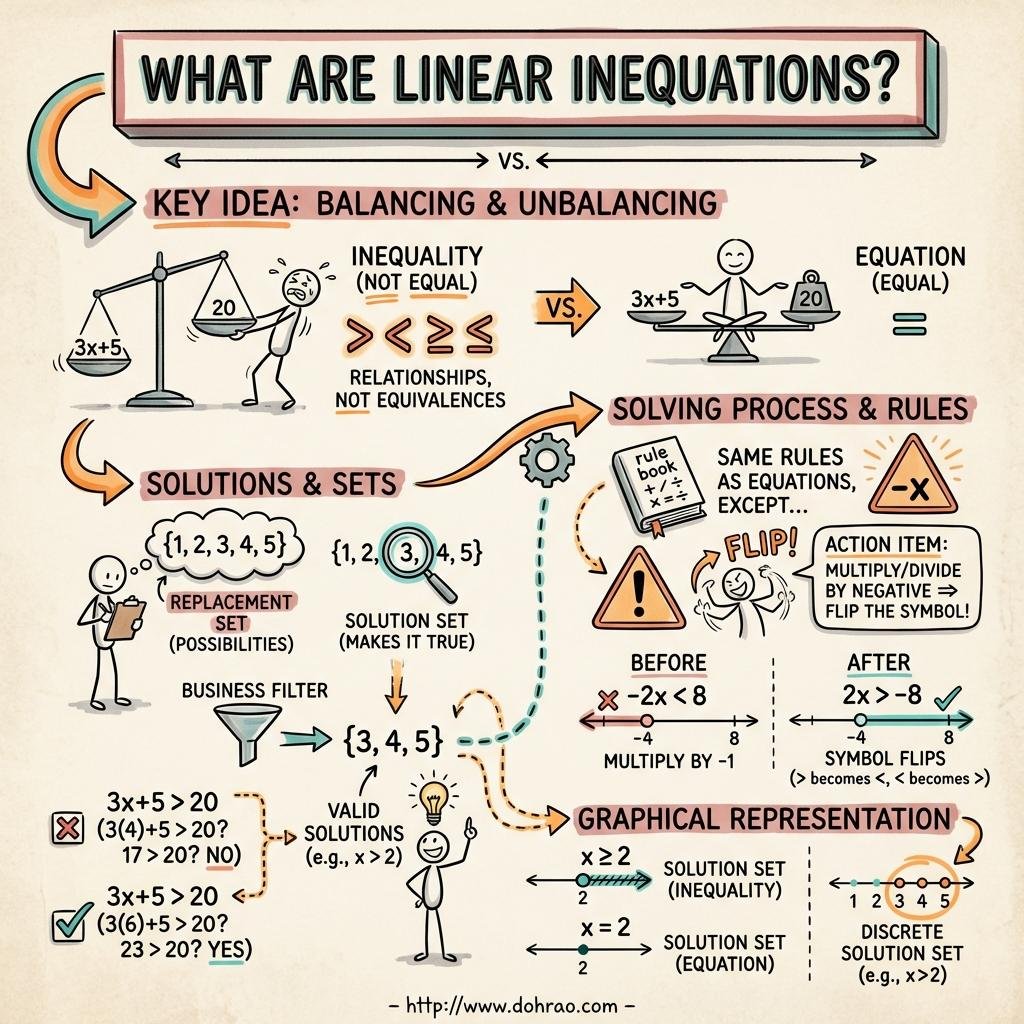
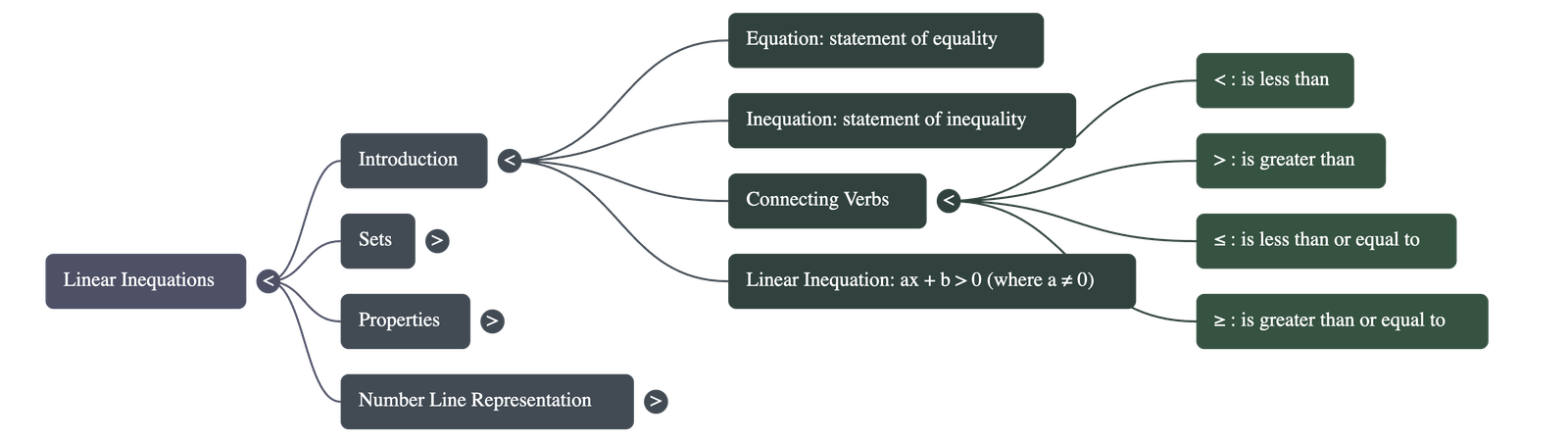
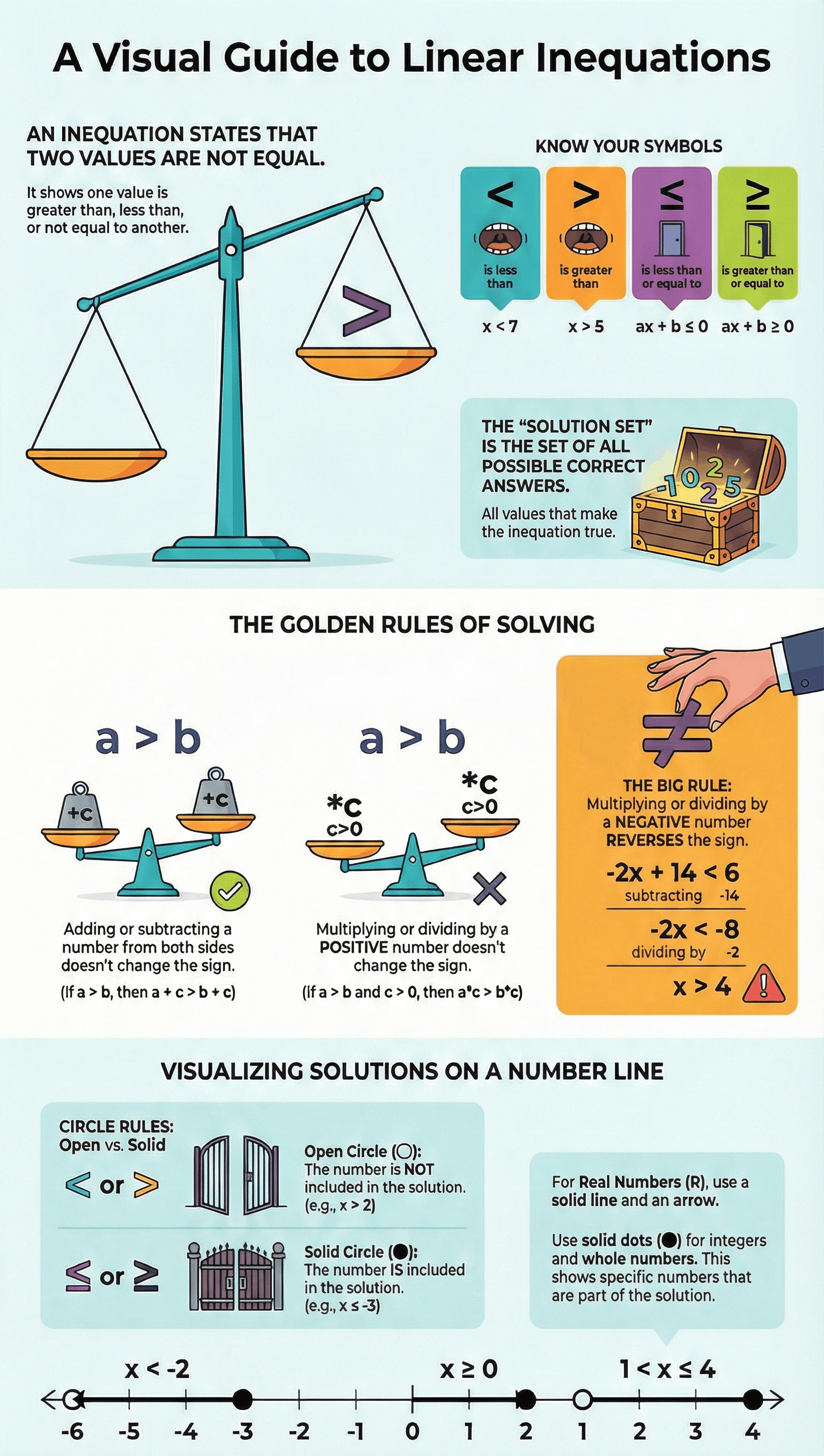
• Equation vs. Inequation: While an equation is a statement of equality (e.g., x = 5), an inequation is a statement showing that one thing is not equal to another, being either greater than or lesser than (e.g., x < 7 or x > 5).
• Connecting Verbs: These are the symbols used to show the relationship between values:
  • < : is less than
  • > : is greater than
  • ≤ : is less than or equal to
  • ≥ : is greater than or equal to
• Linear Inequation: If a and b are real numbers (and a is not zero), expressions like ax + b > 0 or ax + b ≤ 0 are defined as linear inequations.

2. Sets and Solutions

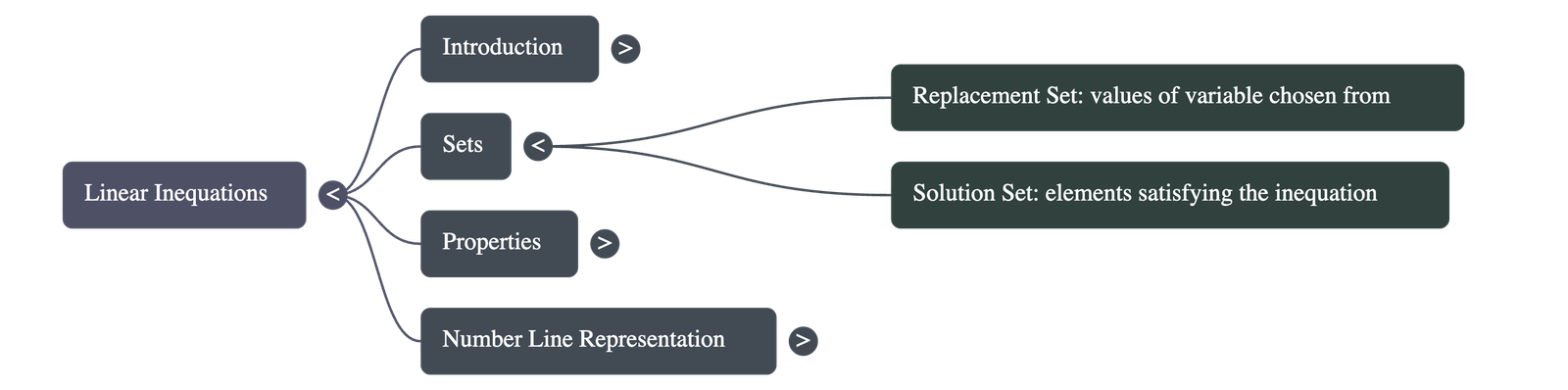
• Replacement Set: Also known as the universal set, this is the set of values from which the variable x is chosen.
• Solution Set: Also known as the truth set, this consists of only the elements from the replacement set that satisfy the given inequation.
• Variable Nature: The solution set changes depending on whether the replacement set consists of Natural numbers (N), Whole numbers (W), Integers (Z), or Real numbers (R).

3. Properties of Inequations

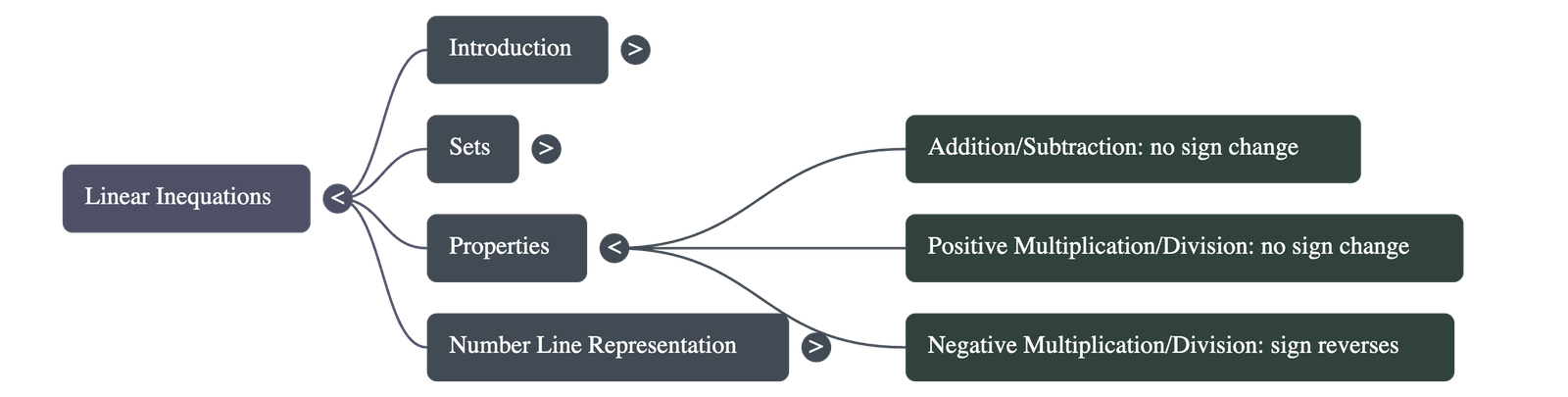
• Addition and Subtraction: Adding or subtracting the same number from both sides of an inequation does not change the sign of inequality.
• Positive Multiplication/Division: Multiplying or dividing each side by a positive number does not change the sign of inequality.
• Negative Multiplication/Division: Multiplying or dividing each side by a negative number reverses the sign of inequality (e.g., > becomes <).

4. Representation on a Number Line

• Discrete Solutions: For sets like Natural numbers or Integers, the solution is represented by thick dots on the specific numbers that satisfy the inequation.
• Real Number Solutions: When x is a real number, the solution is represented by a dark line.
  • A dark circle indicates that the end-point is included (used for ≤ or ≥).
  • A hollow circle indicates that the end-point is excluded (used for < or >).
• Infinite Solutions: A dark arrow on either end of the number line indicates that the solution set continues infinitely in that direction.