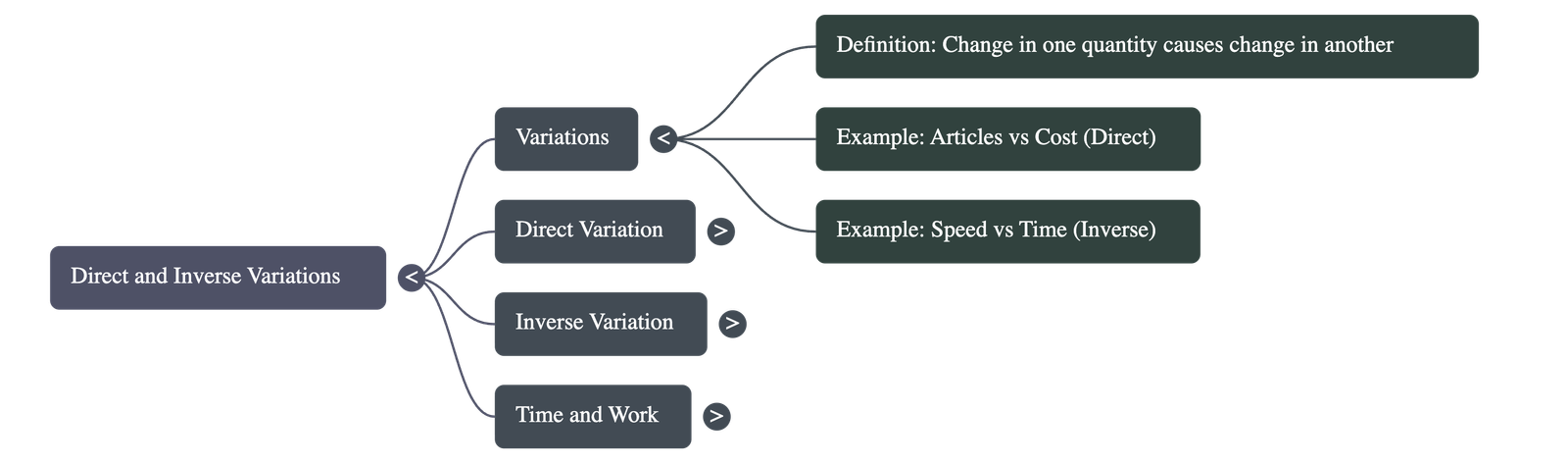
1. Introduction to Variations

• Definition: Two quantities are in variation if a change in one quantity causes a corresponding change in the other.
• Common Examples:
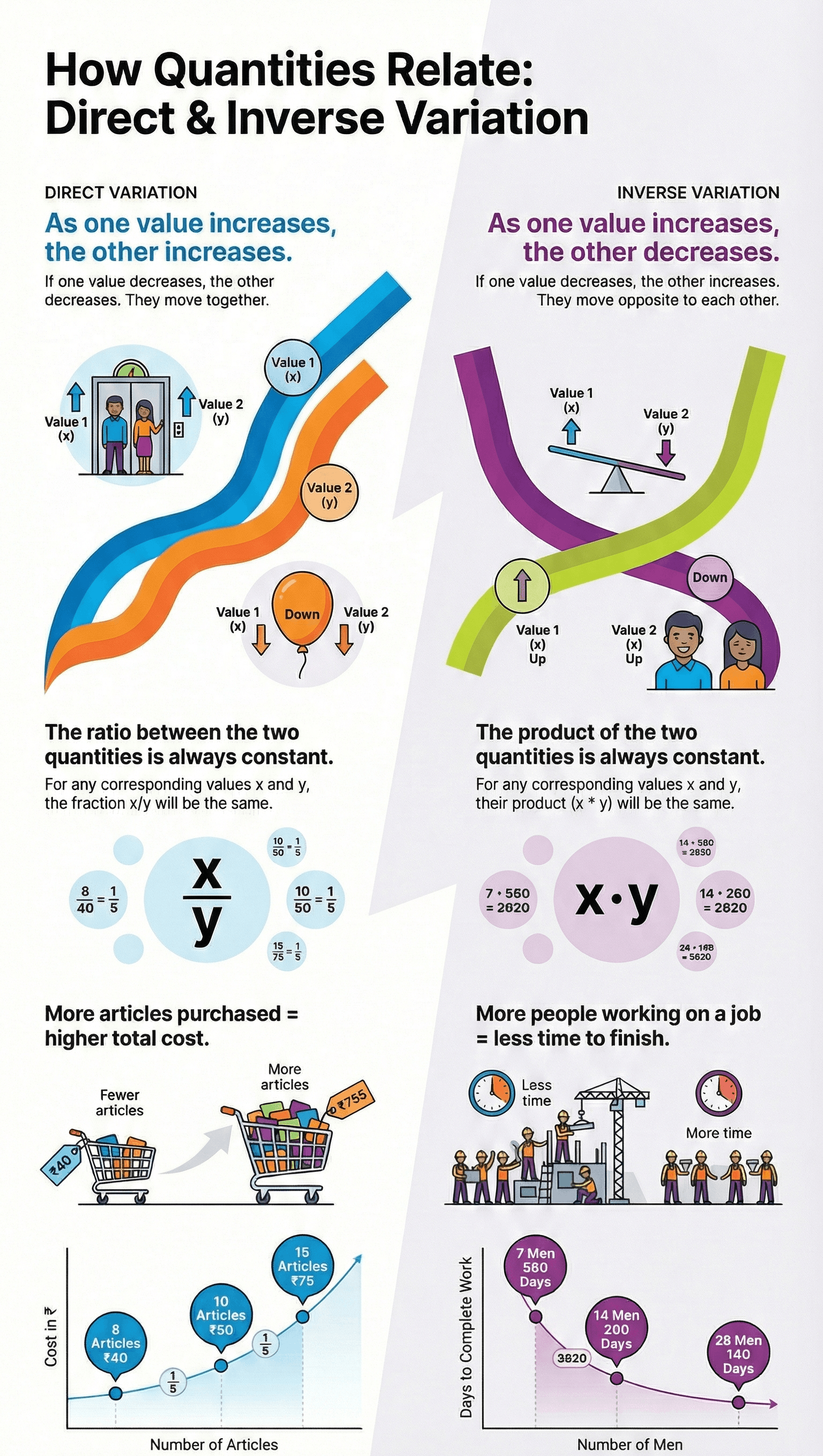
  • The more articles you buy, the higher the total cost.
  • The more money deposited in a bank, the more interest is earned.
  • The higher the speed of a car, the less time it takes to cover a specific distance.

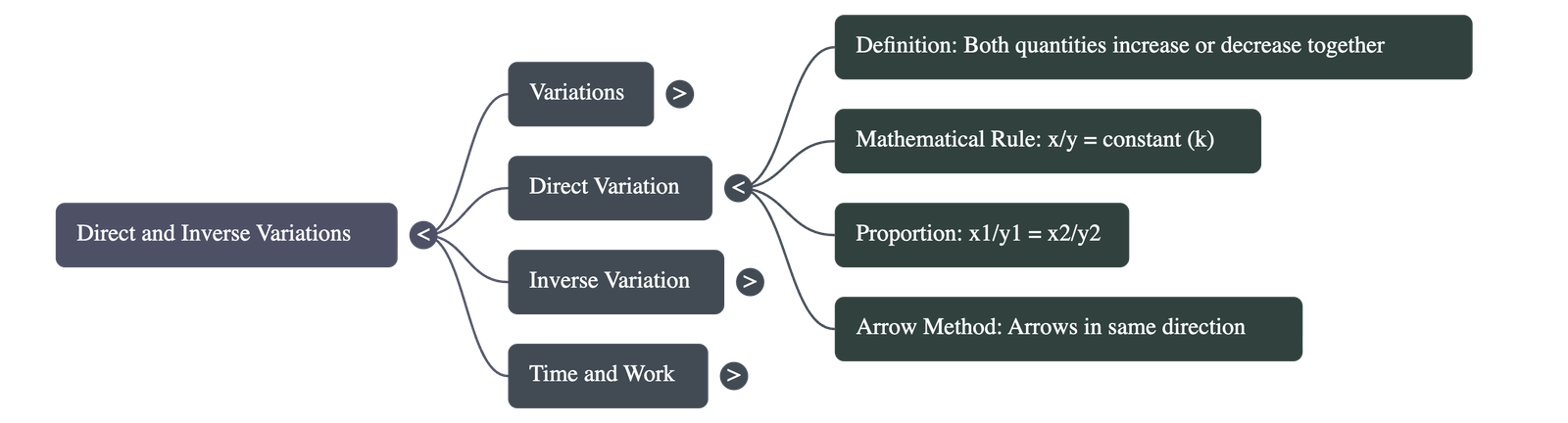
2. Direct Variation

• Concept: Direct variation occurs when an increase in one quantity causes an increase in the other, or a decrease in one causes a decrease in the other.
• Mathematical Rule: If two quantities x and y vary directly, their ratio (x/y) remains constant.
• Formula: x₁ / y₁ = x₂ / y₂ = constant.
• Arrow Method: When solving problems, arrows for both quantities are marked in the same direction (either both upward or both downward).

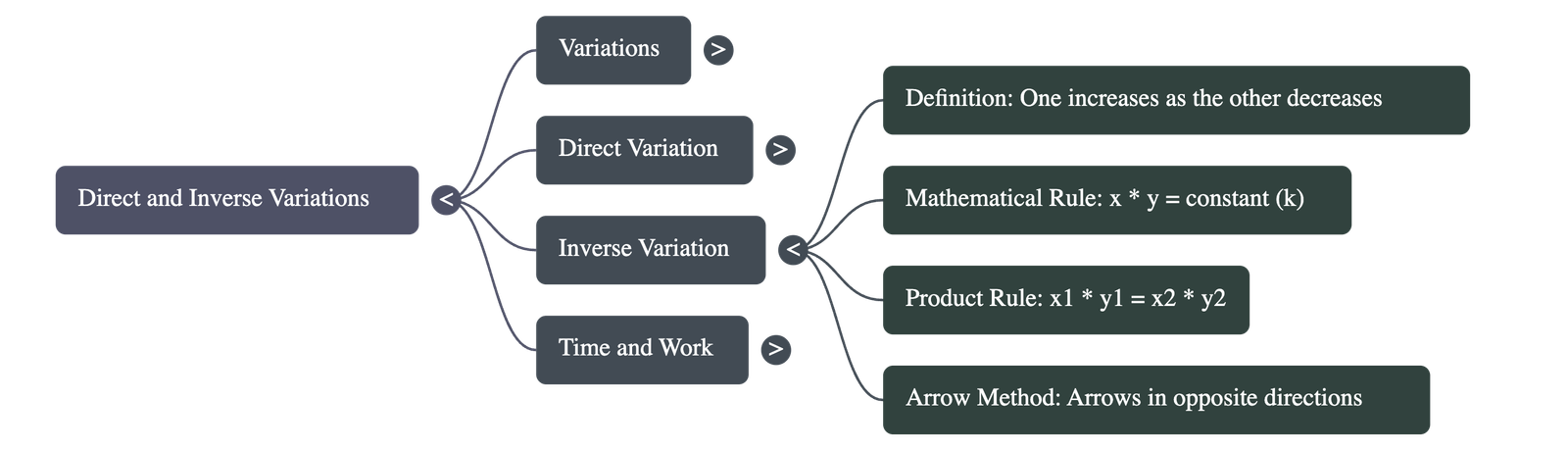
3. Inverse Variation

• Concept: Inverse variation occurs when an increase in one quantity causes a decrease in the other, or a decrease in one causes an increase in the other.
• Mathematical Rule: If two quantities x and y vary inversely, their product (x × y) remains constant.
• Formula: x₁y₁ = x₂y₂ = constant.
• Arrow Method: In calculations, arrows are marked in opposite directions (one upward and one downward).

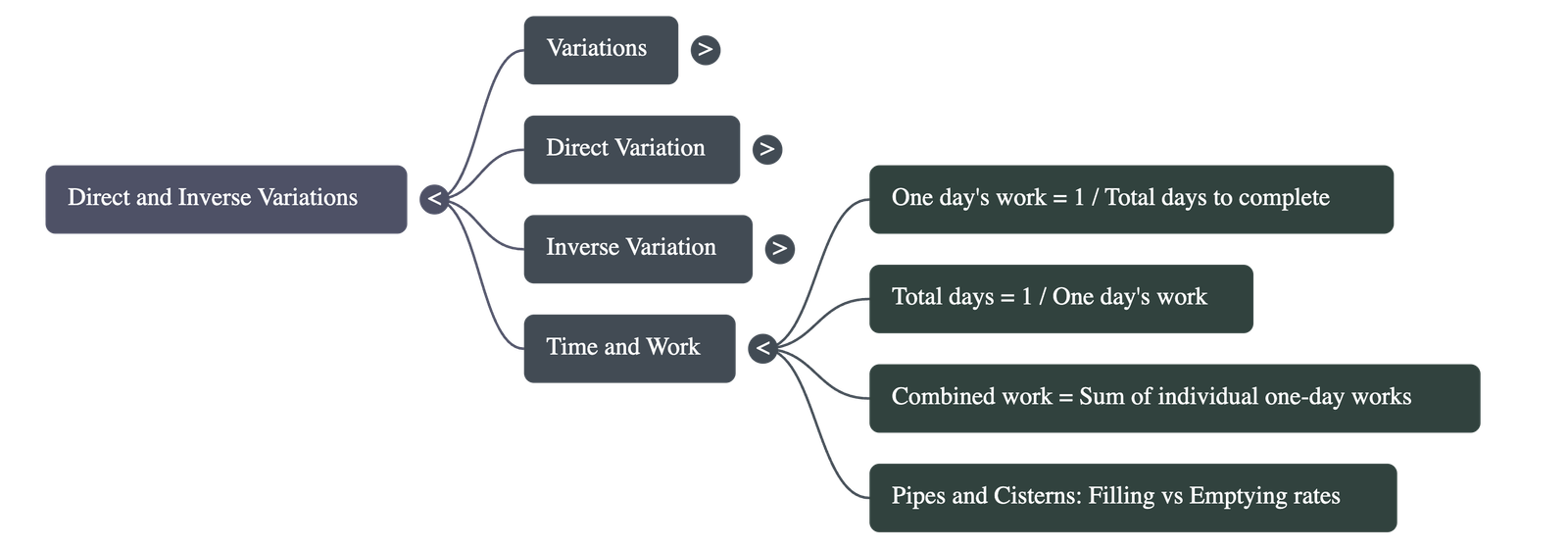
4. Time and Work Concepts

• One Day's Work: If a person can complete a piece of work in n days, then the work done in one day is 1/n.
• Total Time: Conversely, if a person's one day's work is 1/n, they will require n days to finish the entire task.
• Combined Work: When multiple people work together, their individual one-day work rates are added to find the total work done in one day.
• Formula for Time: Number of days required = (Total work to be completed) / (One day's work).

5. Pipes and Cisterns

• Filling Pipes: The work done by a pipe filling a tank is considered positive. If a pipe fills a tank in x minutes, it fills 1/x part of the tank in one minute.
• Emptying Pipes (Waste Pipes): The work done by a pipe emptying a tank is considered negative. If a pipe empties a full tank in y minutes, it empties 1/y part of the tank in one minute.
• Net Work: If multiple pipes are open at once, the net rate of filling or emptying is the sum of the rates of the filling pipes minus the rates of the emptying pipes.