Chapter Summary: Exponents (Powers)

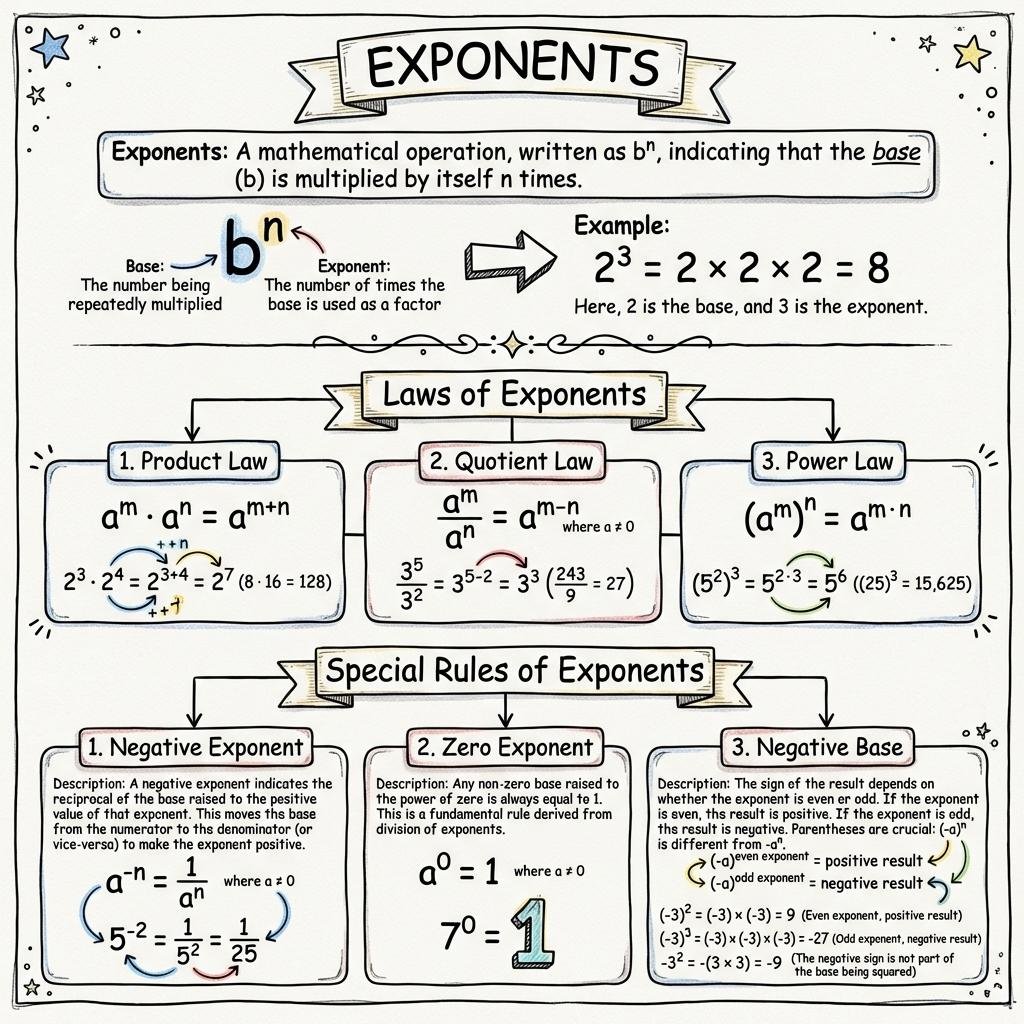
1. Fundamental Concepts

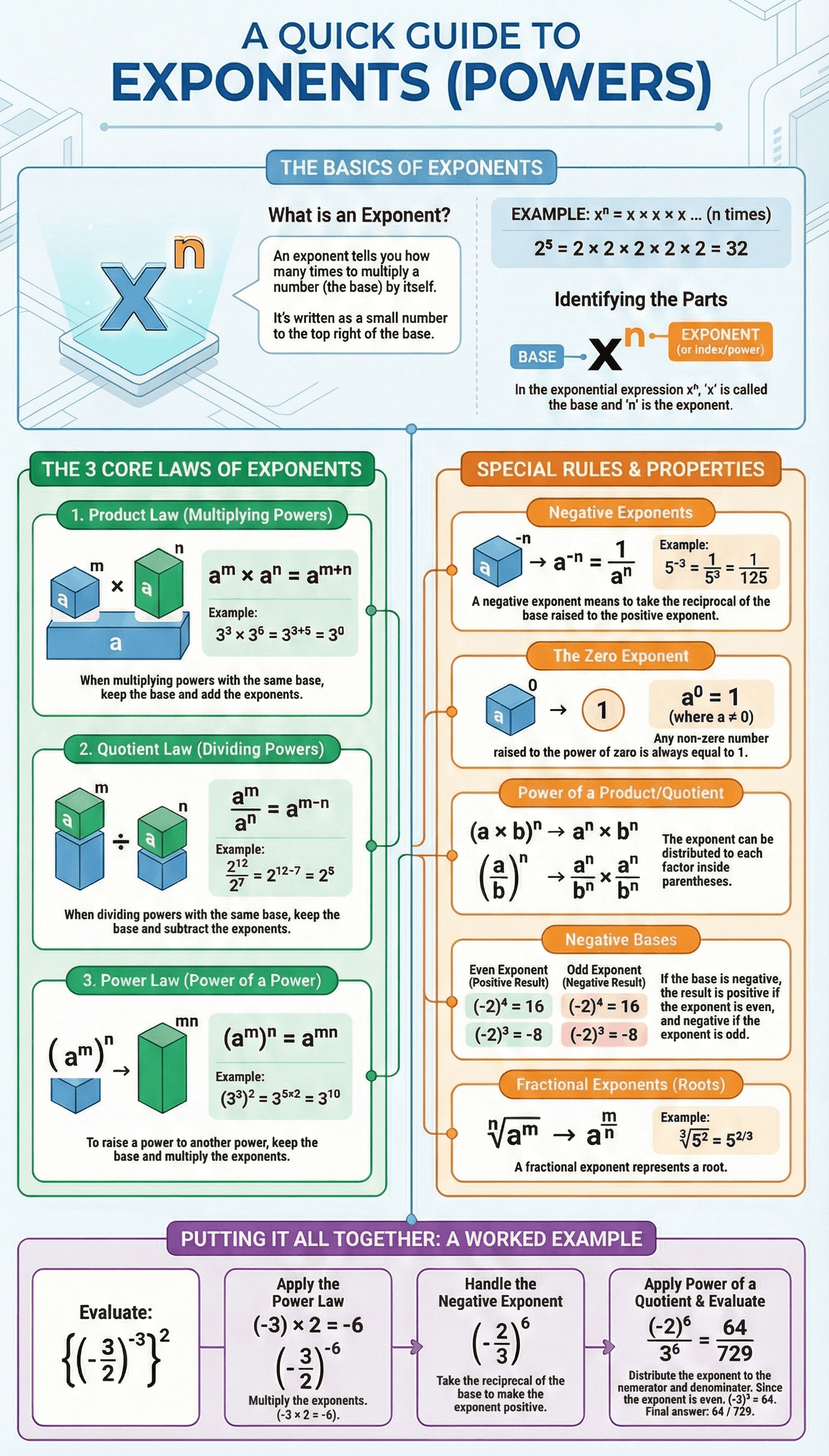
• Exponential Notation: If x is a real number and n is an integer, xⁿ represents x multiplied by itself n times.
• Components: In the expression xⁿ, x is the base and n is the exponent (also known as the index or power).
• Reading Notation: The term is read as "x raised to the power n."

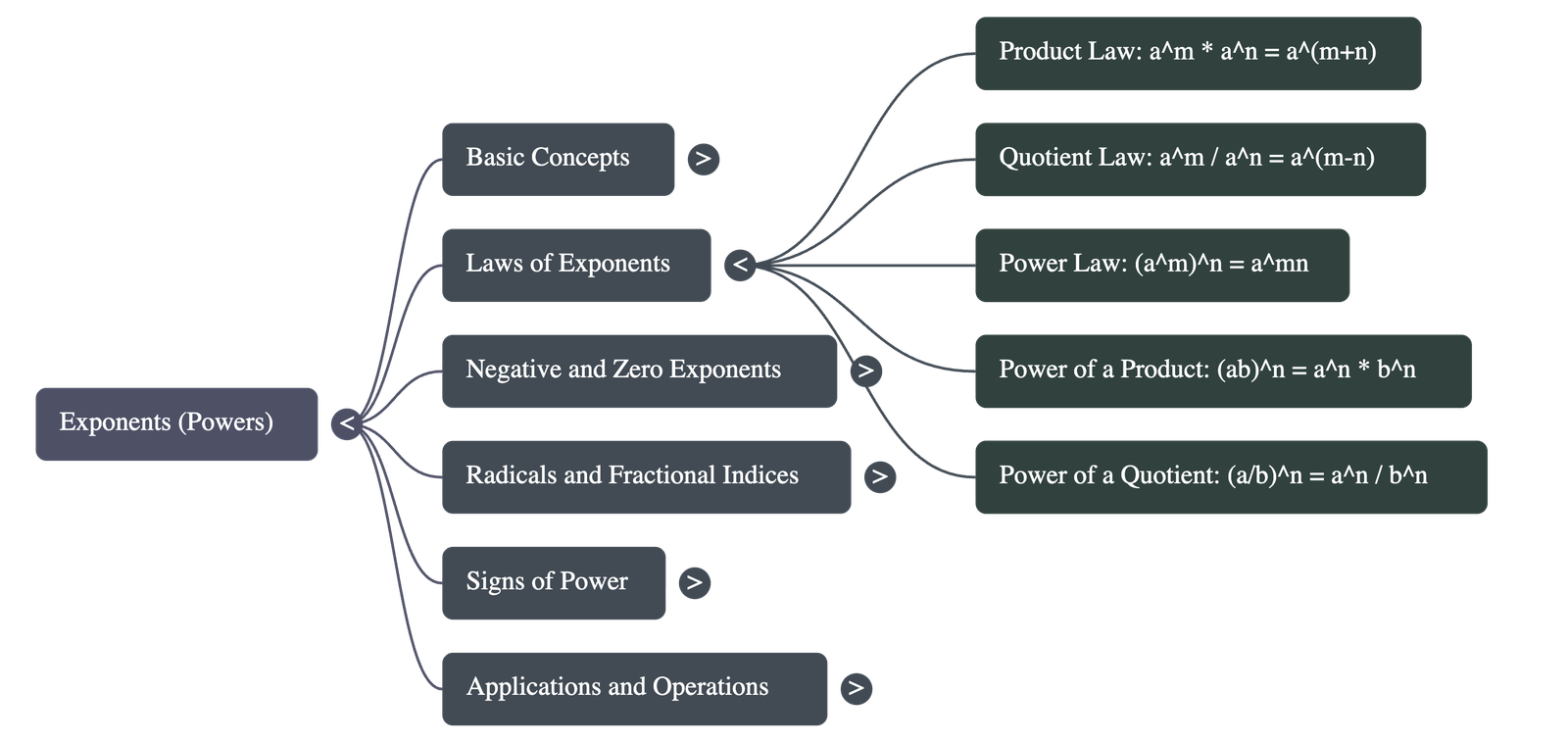
2. Laws of Exponents

• Product Law: When multiplying powers with the same base, add the exponents: a^m × aⁿ = a^m+n.
• Quotient Law: When dividing powers with the same base, subtract the exponents: a^m ÷ aⁿ = a^m-n.
• Power Law: To raise a power to another power, multiply the exponents: (a^m)ⁿ = a^mn.
• Power of a Product: The exponent applies to every factor inside the parentheses: (ab)ⁿ = aⁿbⁿ.
• Power of a Quotient: The exponent applies to both numerator and denominator: (a/b)ⁿ = aⁿ / bⁿ.

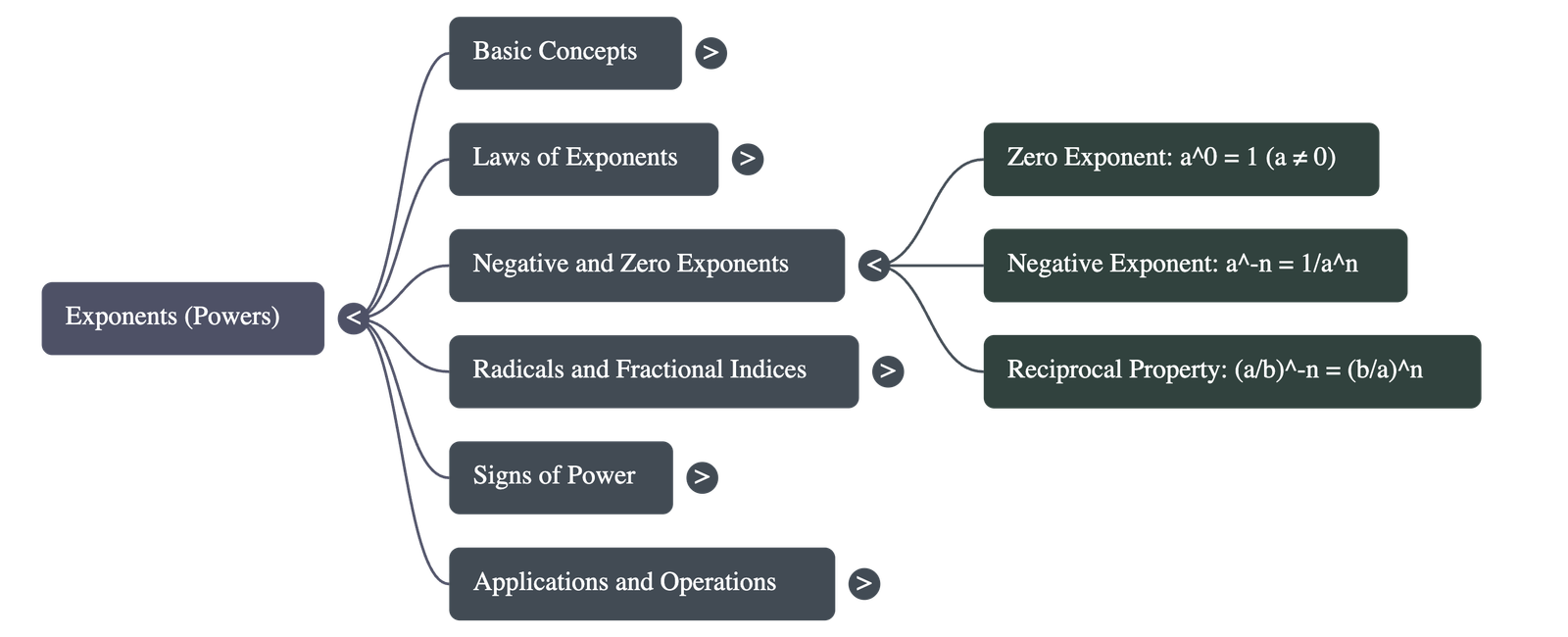
3. Negative and Zero Exponents

• Zero Exponent: Any non-zero number raised to the power of zero is always equal to 1 (a⁰ = 1).
• Negative Exponent: A negative exponent indicates the reciprocal of the base: a^-n = 1/aⁿ.
• Reciprocal Relationship: a^-n and aⁿ are reciprocals of each other.
• Notation Caution: Note the difference in signs: (-a)⁰ is 1, while -a⁰ is -1.