1. Fundamental Concepts of Interest

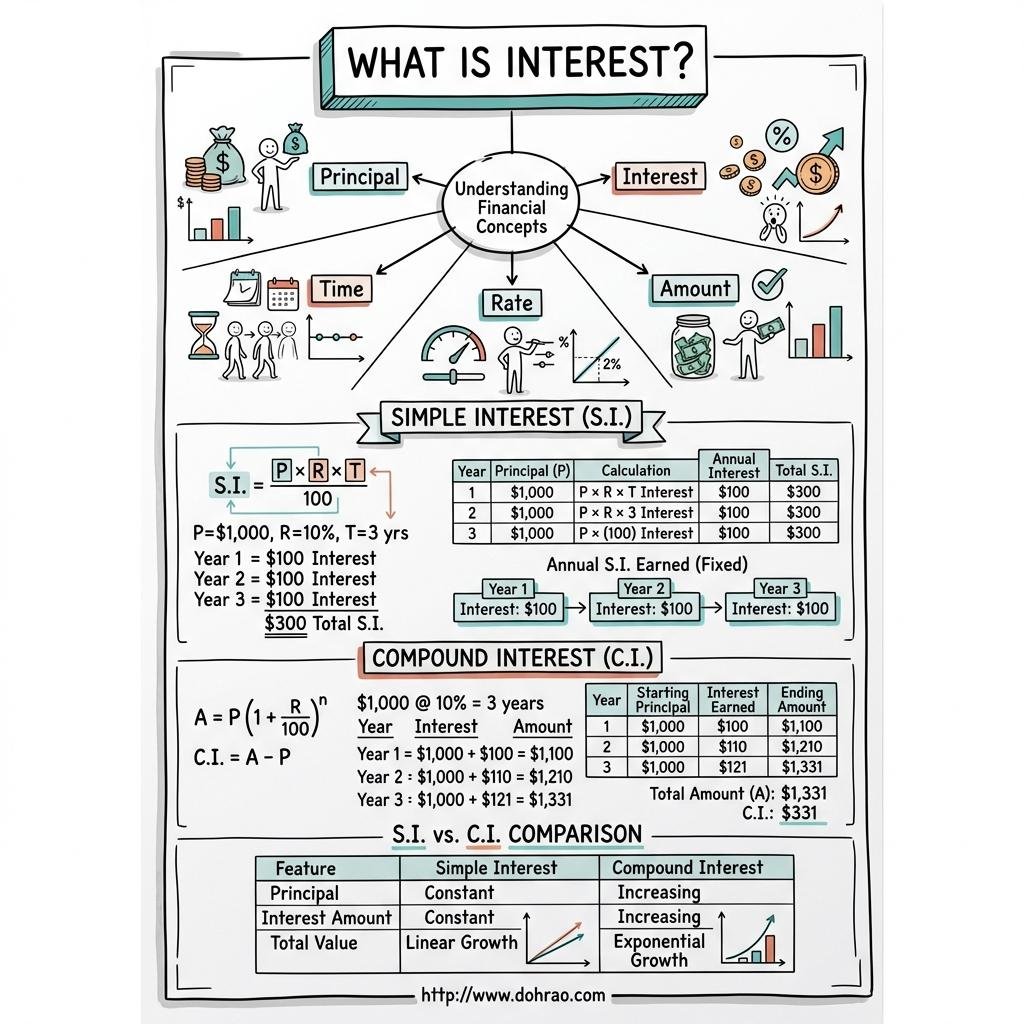
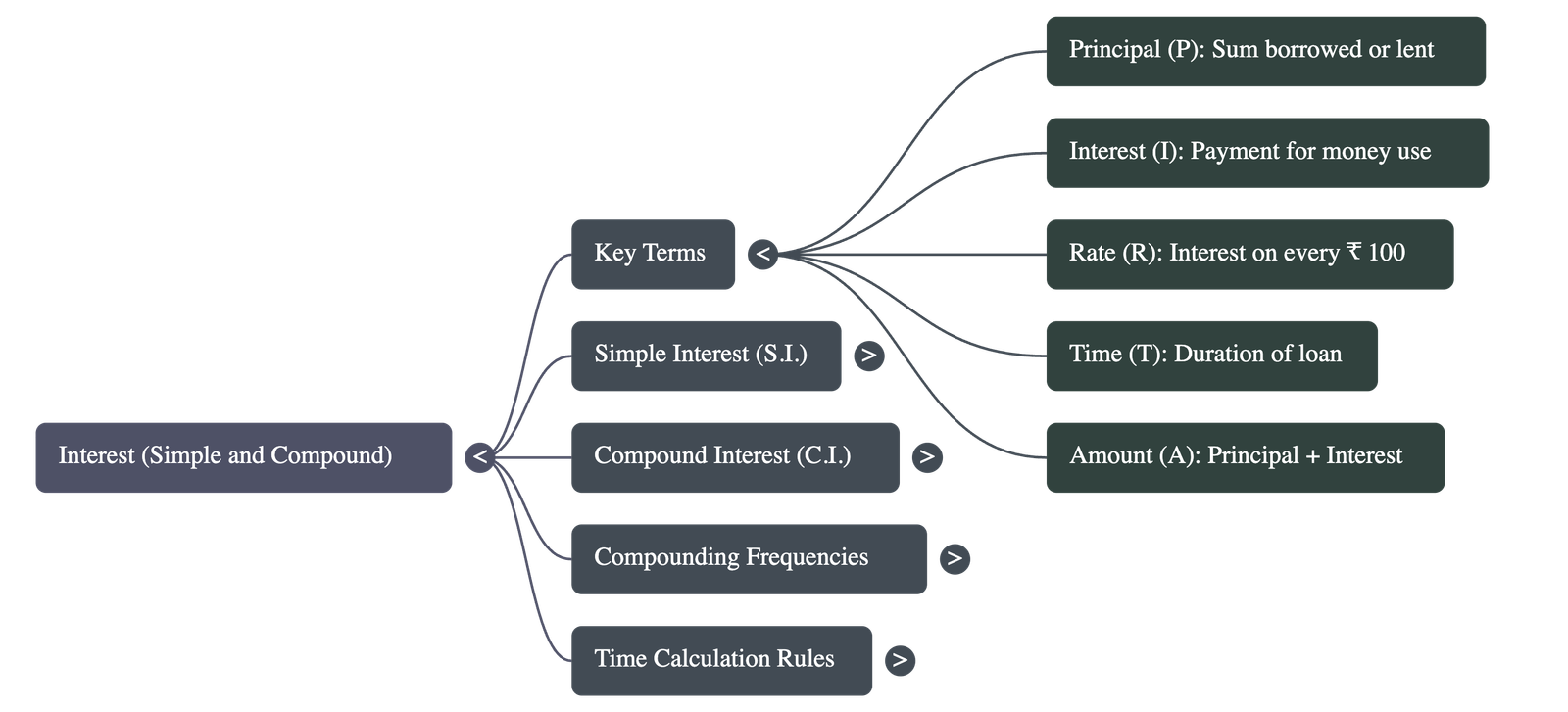
• Principal (P): The sum of money borrowed from or lent to another party.
• Interest (I): The additional money paid by a borrower to a lender for the use of the principal.
• Rate (R): The interest charged on every ₹100, typically expressed as a percentage per annum (per year) or per month.
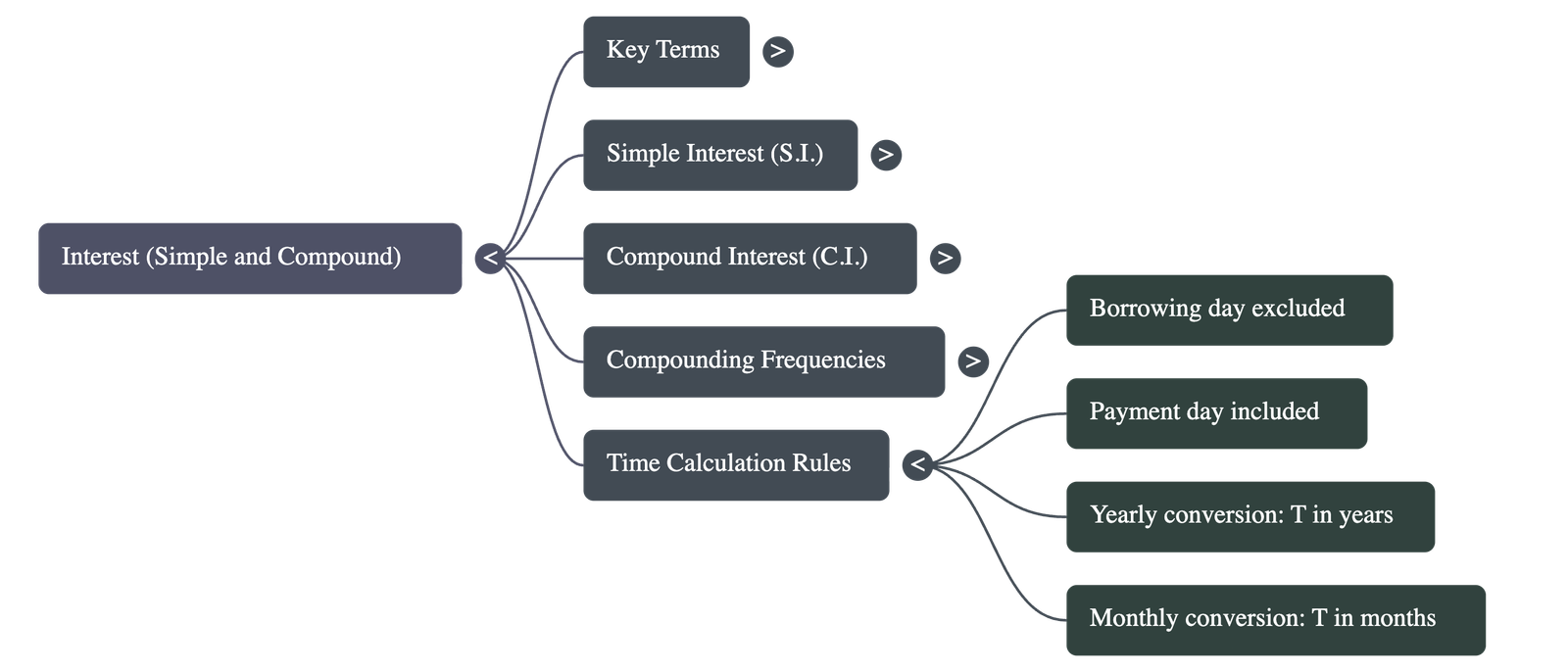
• Time (T): The duration for which the money is lent or borrowed. If the rate is per year, time must be calculated in years; if the rate is per month, time must be in months.
• Amount (A): The total sum of the principal and the interest earned (A = P + I).

2. Simple Interest (S.I.)

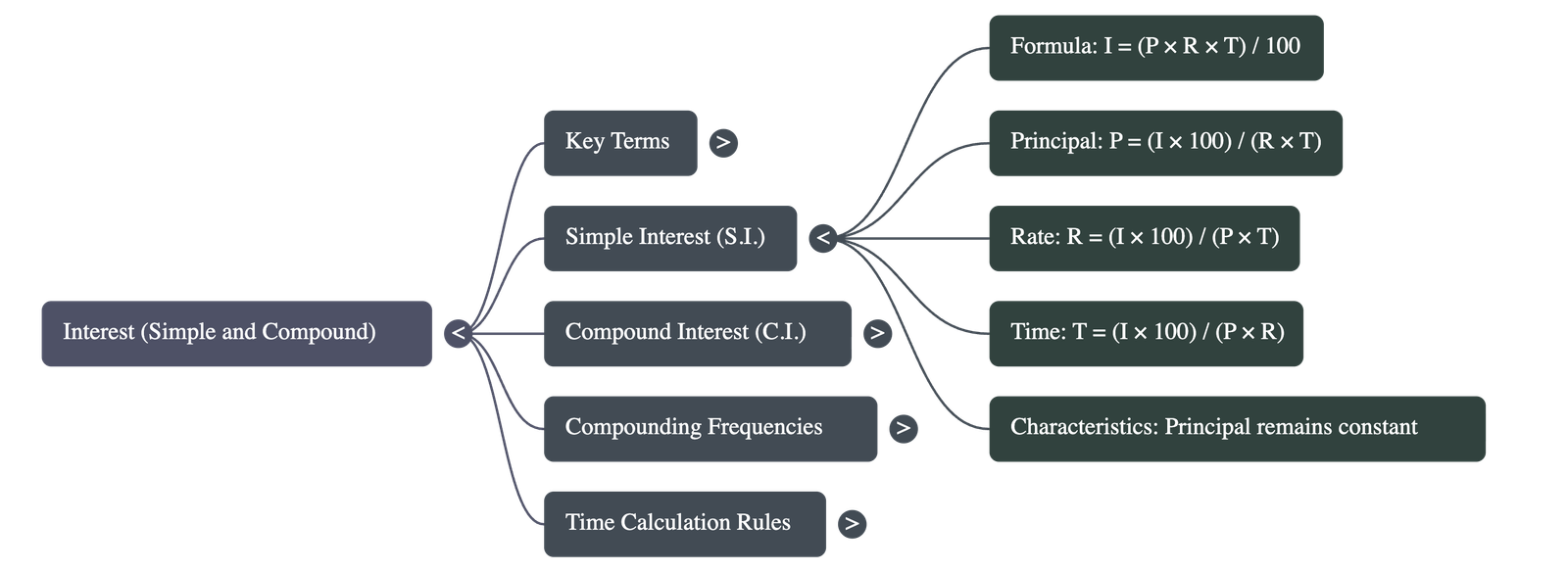
• Simple interest is calculated uniformly on the original principal throughout the entire loan period.
• Core Formula: Interest (I) = (P × R × T) / 100.
• Derived Formulas:
  • To find Principal: P = (I × 100) / (R × T)
  • To find Rate: R = (I × 100) / (P × T)
  • To find Time: T = (I × 100) / (P × R)
• Time Calculation Rule: When calculating interest by days, the day the money is borrowed is excluded, but the day the money is returned is included.

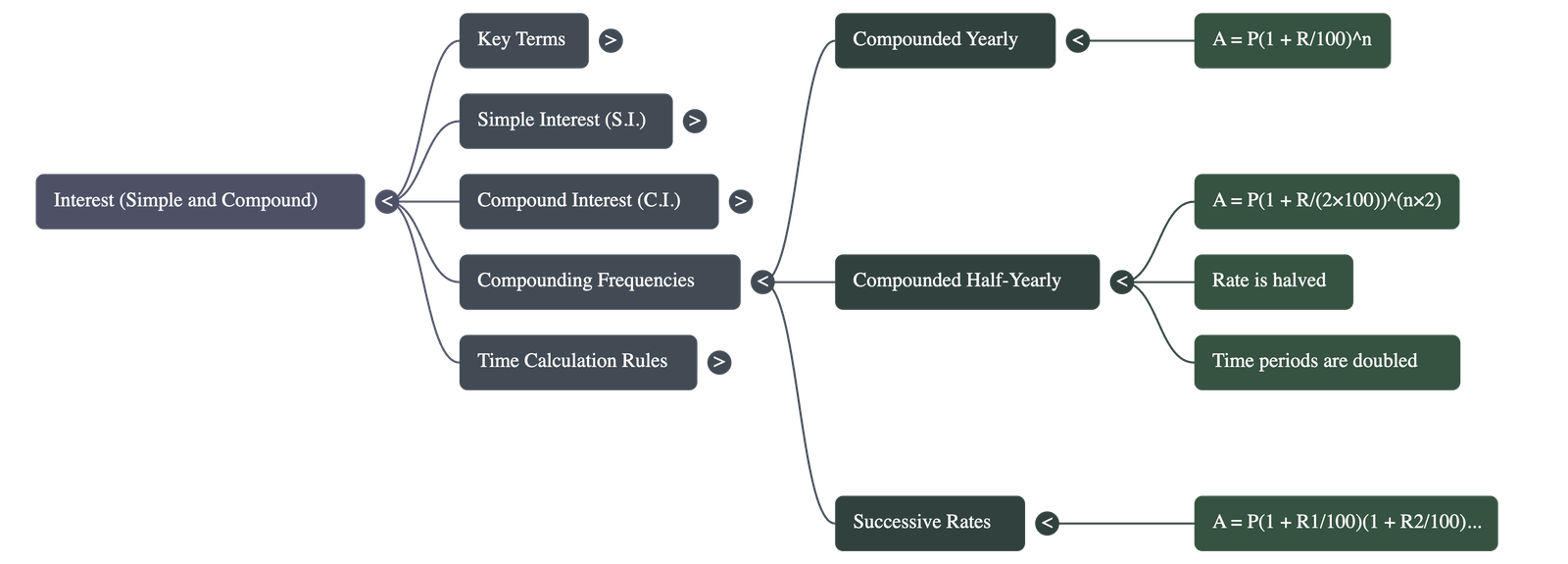
3. Compound Interest (C.I.) - The Method

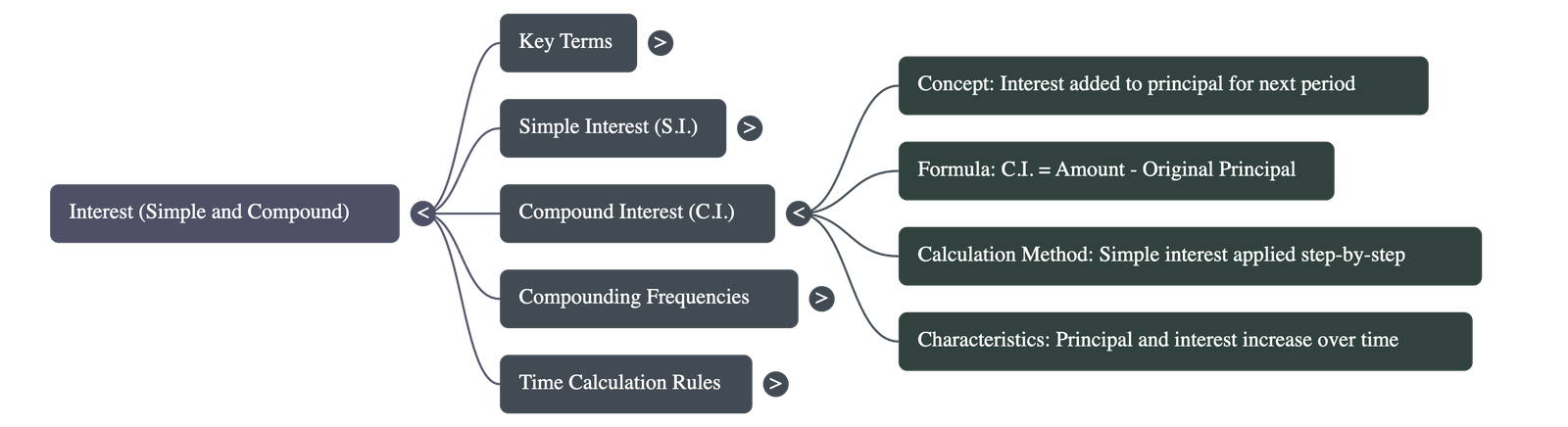
• Concept: Unlike simple interest, compound interest involves adding the interest earned at the end of a specific period to the principal to form a new principal for the next period.
• Calculation: The process is repeated for the duration of the loan. The final compound interest is the difference between the final amount and the original principal (C.I. = A - P).
• Comparison: In simple interest, the principal remains constant every year. In compound interest, the principal increases every year, and consequently, the interest earned also increases each year.

4. Compounding Variations

• Half-Yearly Compounding: Interest can be calculated and added to the principal every six months. In this case, the time period is doubled and the rate is effectively halved for each calculation step.
• Successive Rates: If the interest rate changes every year (e.g., R1 for the first year, R2 for the second), the amount is calculated by applying each rate consecutively to the growing principal.

5. Standard Formulae for Compound Interest

• Compounded Yearly: A = P(1 + R/100)ⁿ, where 'n' is the number of years.
• Compounded Half-Yearly: A = P(1 + R / (2 × 100))^{n × 2}.
• Successive Rates for 3 Years: A = P(1 + R1/100)(1 + R2/100)(1 + R3/100).