Quick Navigation:
| | | | |
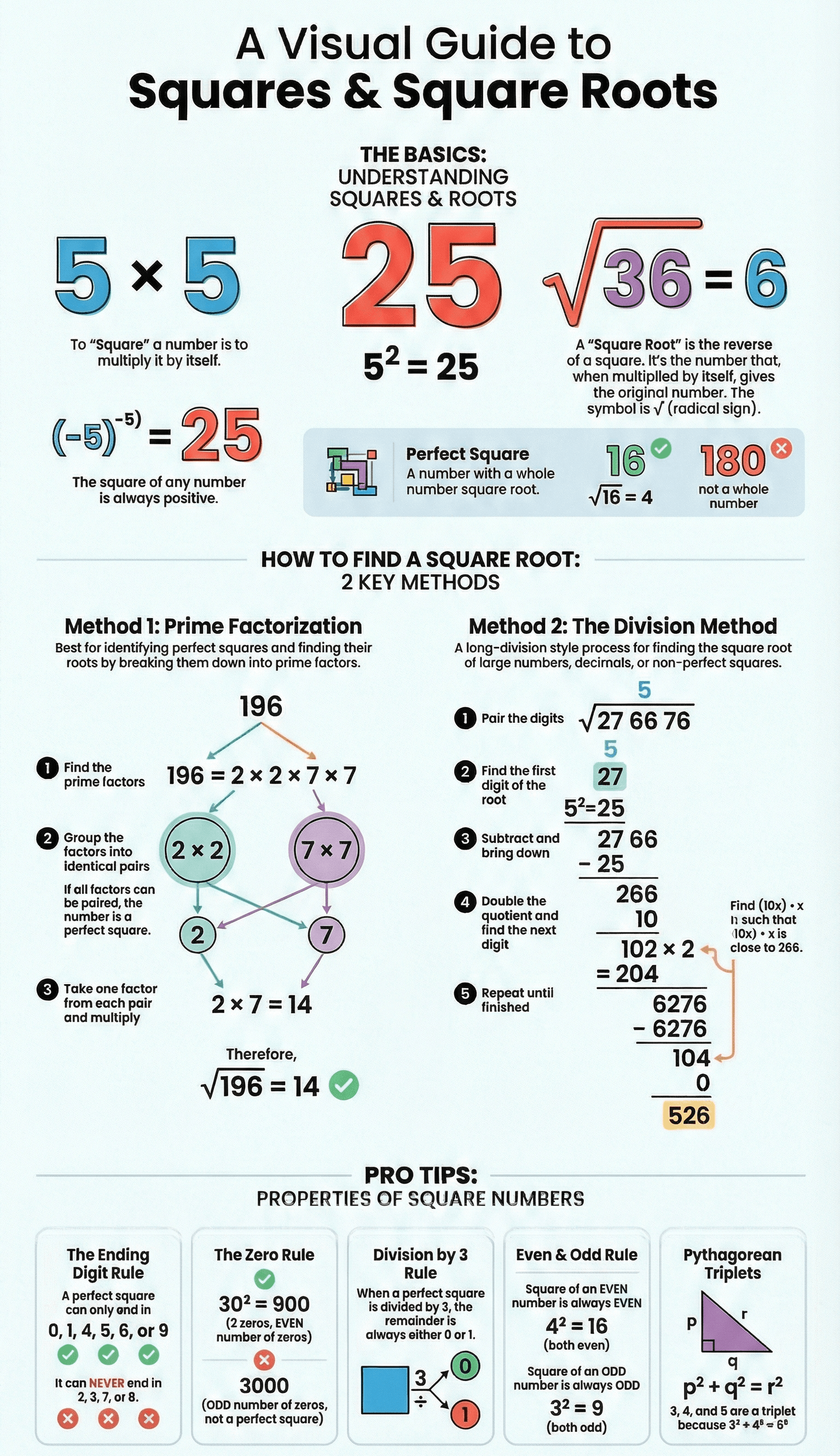
Quick Navigation:
| | | | |
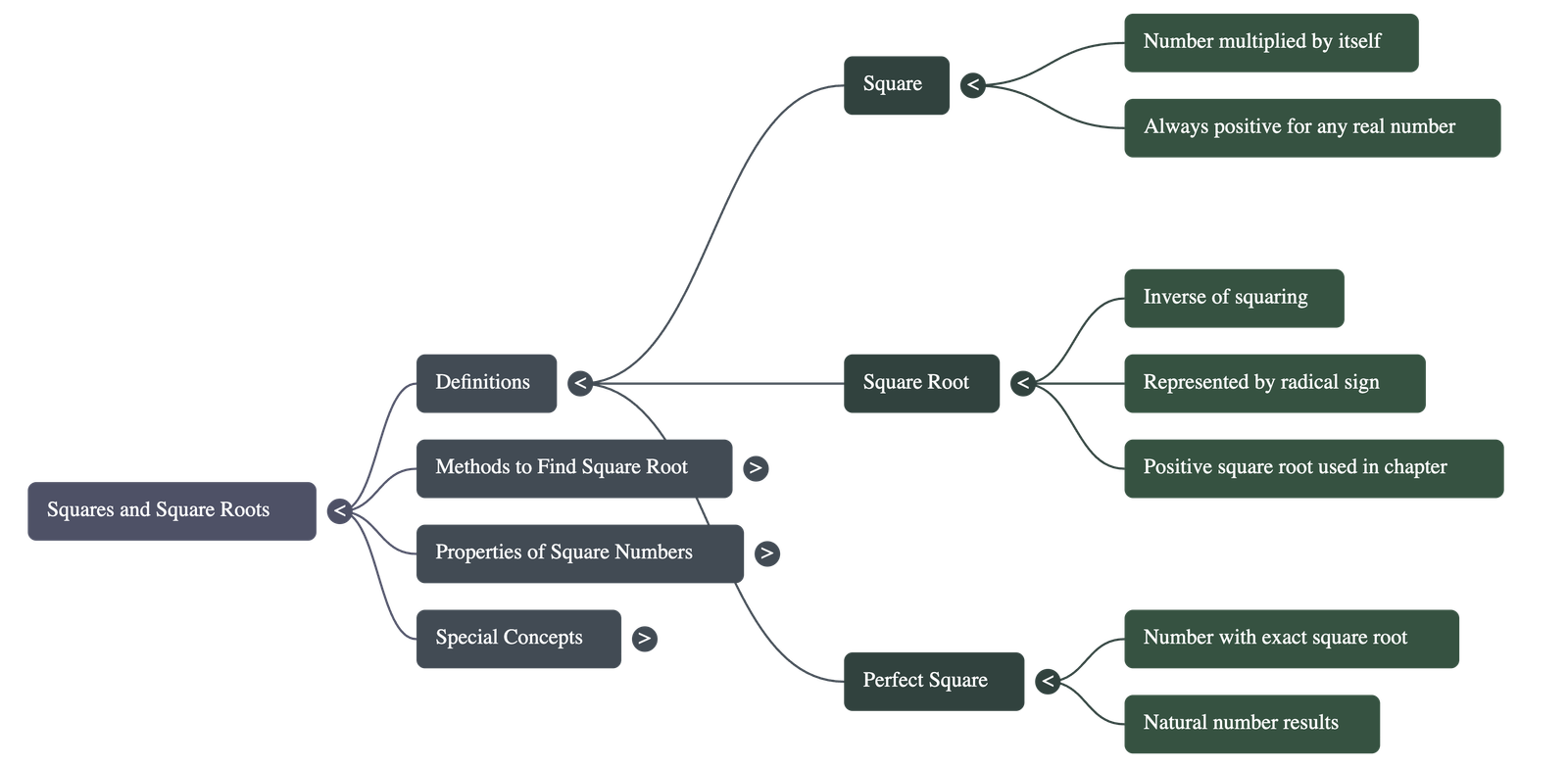
1. Fundamental Concepts
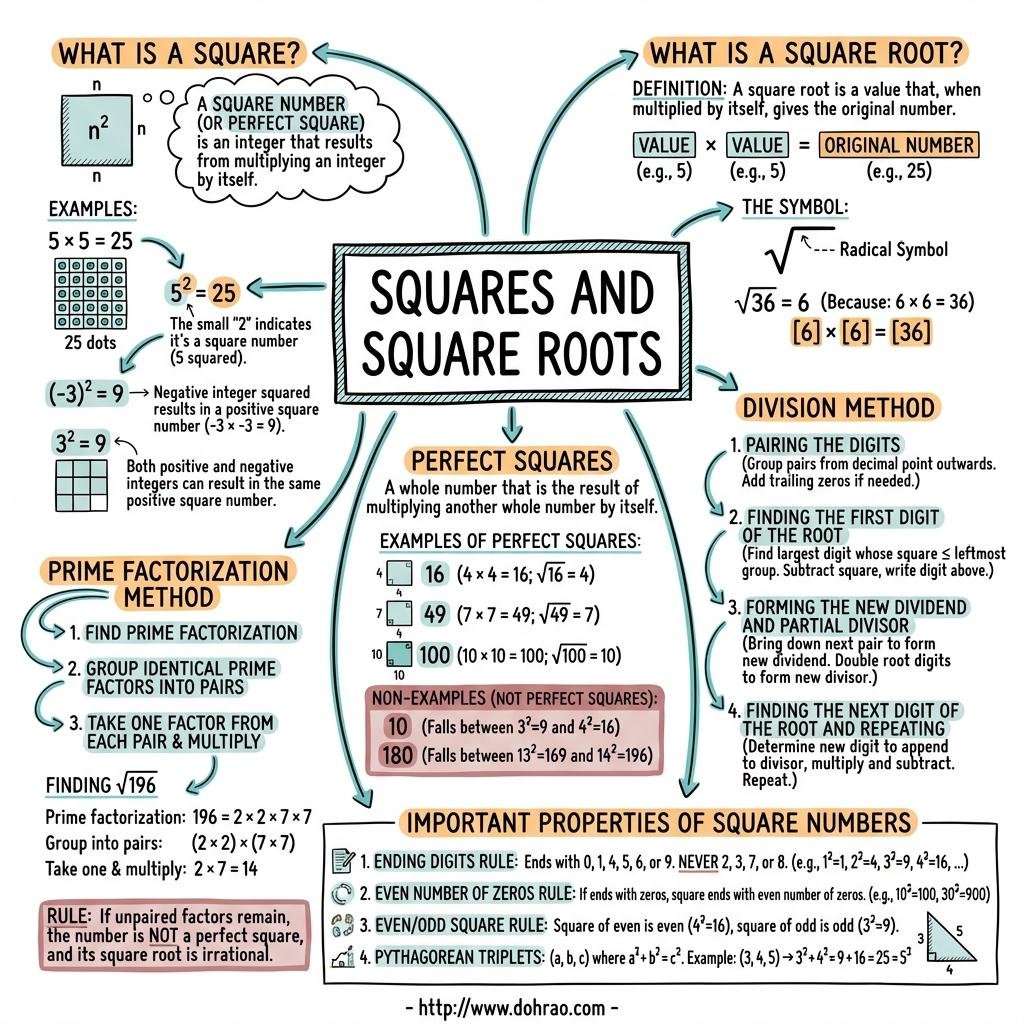
- Square: The product obtained when a number is multiplied by itself. For example, the square of 5 is 25.
- Square Root: The number which, when squared, results in the original value. It is represented by the radical sign √.
- Perfect Square: A number whose exact square root can be obtained, such as 16, 49, or 1.21.
- General Rules:
- Squares of even numbers are always even; squares of odd numbers are always odd.
- The square of any number (positive or negative) is always positive.
- Square roots of negative numbers are not possible within the scope of this chapter.
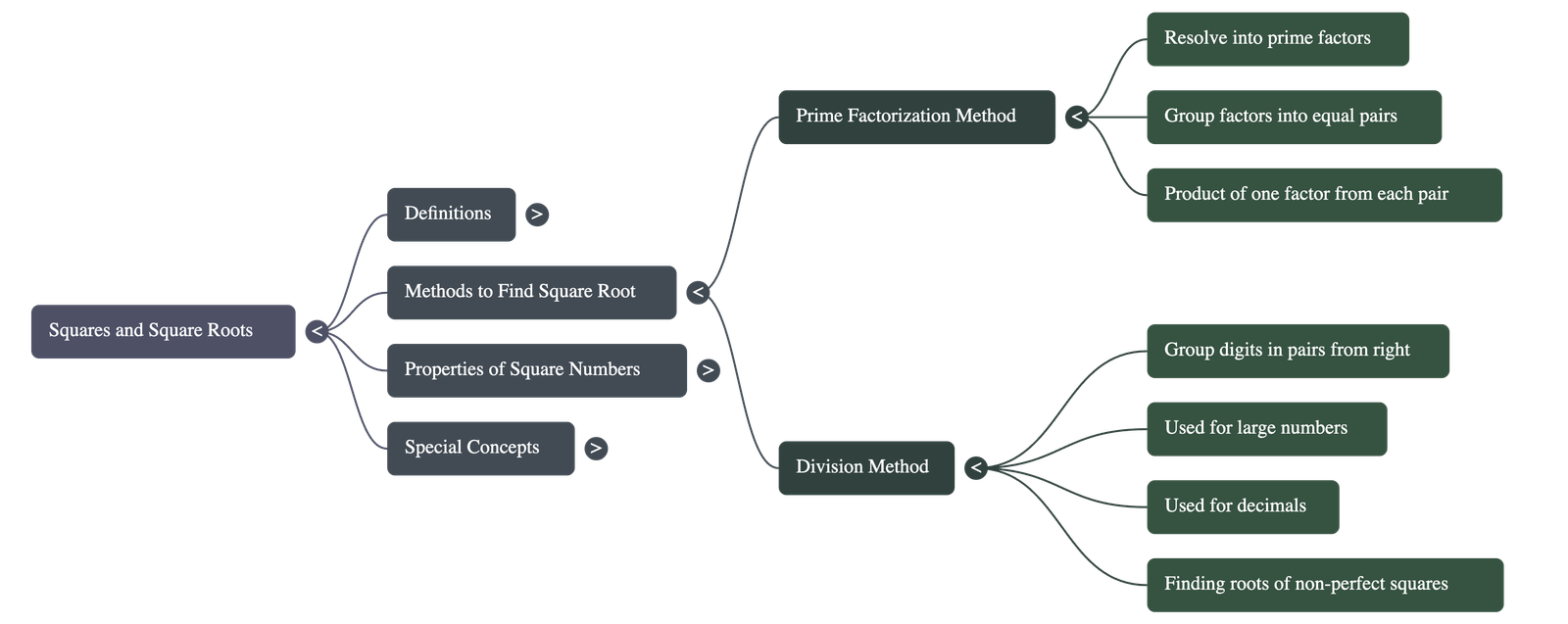
2. Methods to Find Square Roots
- Prime Factor Method: Resolve the number into its prime factors and group them into identical pairs. The product of one factor from each pair is the square root. If a factor remains unpaired, the number is not a perfect square.
- Division Method: Used primarily for large numbers and decimals. Digits are grouped in pairs (called periods) starting from the decimal point.
- For integers, grouping goes from right to left.
- For decimals, grouping goes from left to right.
- Fractional Square Roots: The square root of a fraction is calculated by finding the square root of the numerator and the square root of the denominator separately.
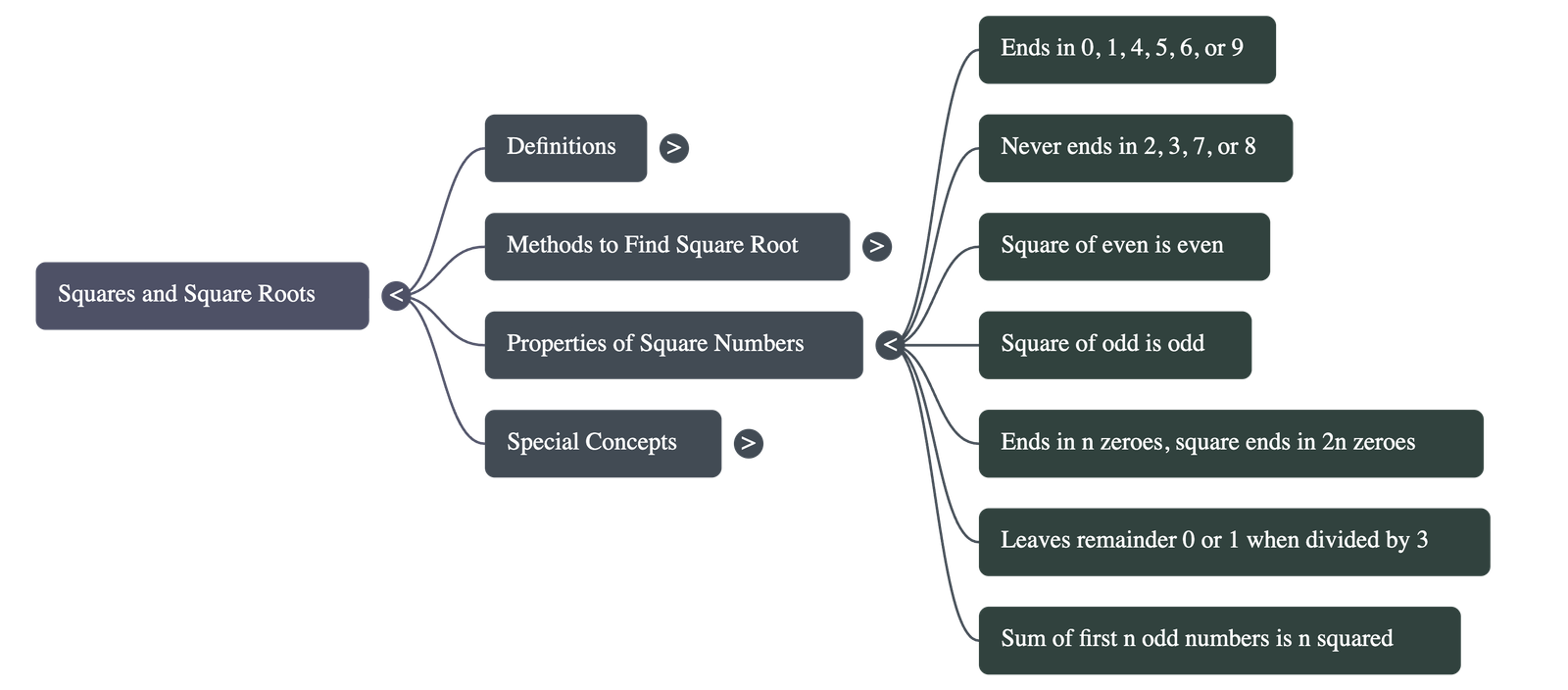
3. Properties of Square Numbers
- Ending Digits: A square number always ends in 0, 1, 4, 5, 6, or 9.
- Impossible Endings: Numbers ending in 2, 3, 7, or 8 are never perfect squares.
- Unit's Place Patterns:
- If a number ends in 1 or 9, its square ends in 1.
- If a number ends in 4 or 6, its square ends in 6.
- Zeroes: If a number ends in n zeroes, its square ends in 2n zeroes (always an even number of zeroes).
- Division by 3: A perfect square, when divided by 3, always leaves a remainder of 0 or 1.
- Decimal Places: The square of a decimal number always contains an even number of decimal places.
4. Special Mathematical Patterns
- Consecutive Squares: For any natural number n, the difference between the squares of two consecutive numbers is equal to their sum: (n + 1)² - n² = (n + 1) + n.
- Sum of Odd Numbers: The sum of the first n odd natural numbers is equal to n².
- Pythagorean Triplets: Three natural numbers (p, q, r) form a triplet if the sum of the squares of two numbers equals the square of the third (p² + q² = r²). For example, 3, 4, and 5.
5. Practical Applications
- Approximation: To find a square root correct to n decimal places, the calculation is carried out to n+1 places and then rounded off.
- Correction to Perfect Squares: The sources detail how to find the least number that must be added to or subtracted from a non-perfect square to make it a perfect square using the division method.
- Divisibility: To find the smallest perfect square divisible by a set of numbers, one finds the L.C.M. and then multiplies it by the required factors to ensure every prime factor is paired.
Quick Navigation:
| | | | |
1 / 1
Quick Navigation:
| | | | |