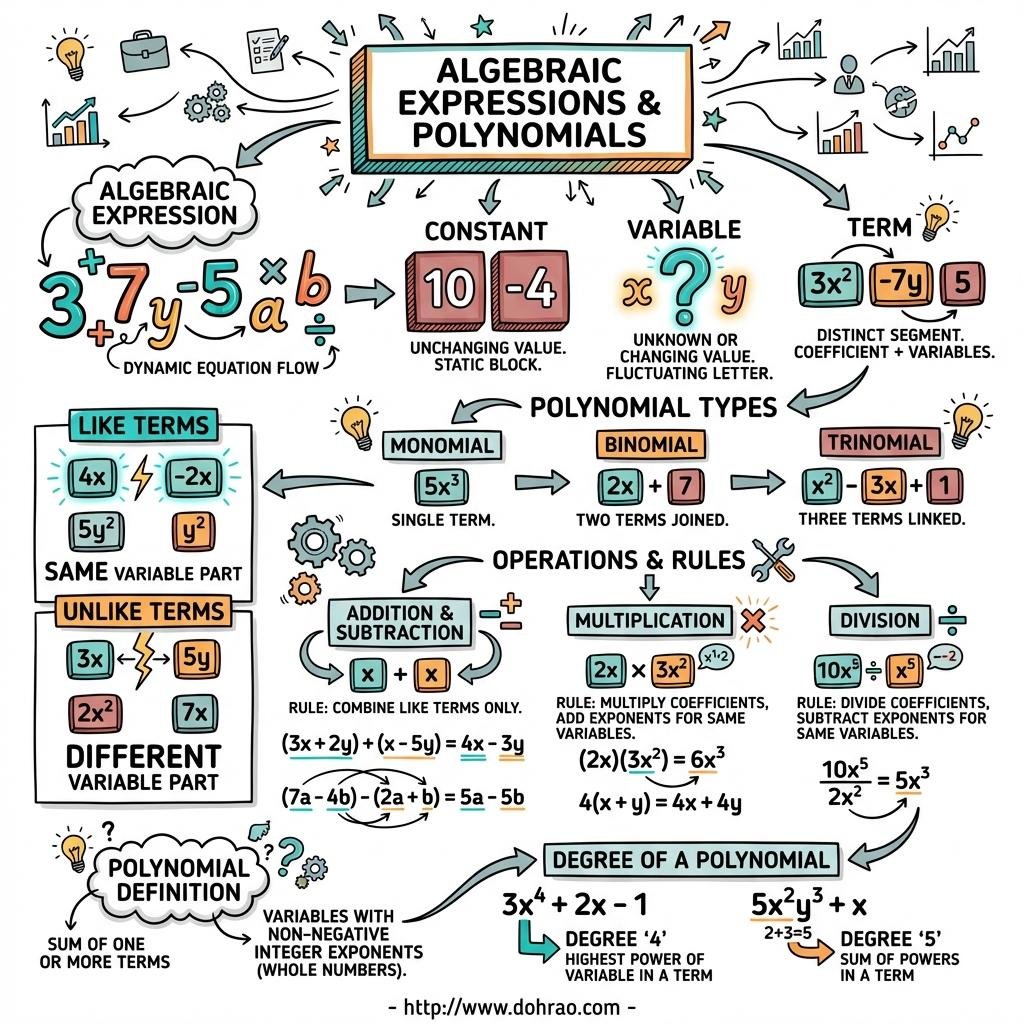
1. Fundamental Components

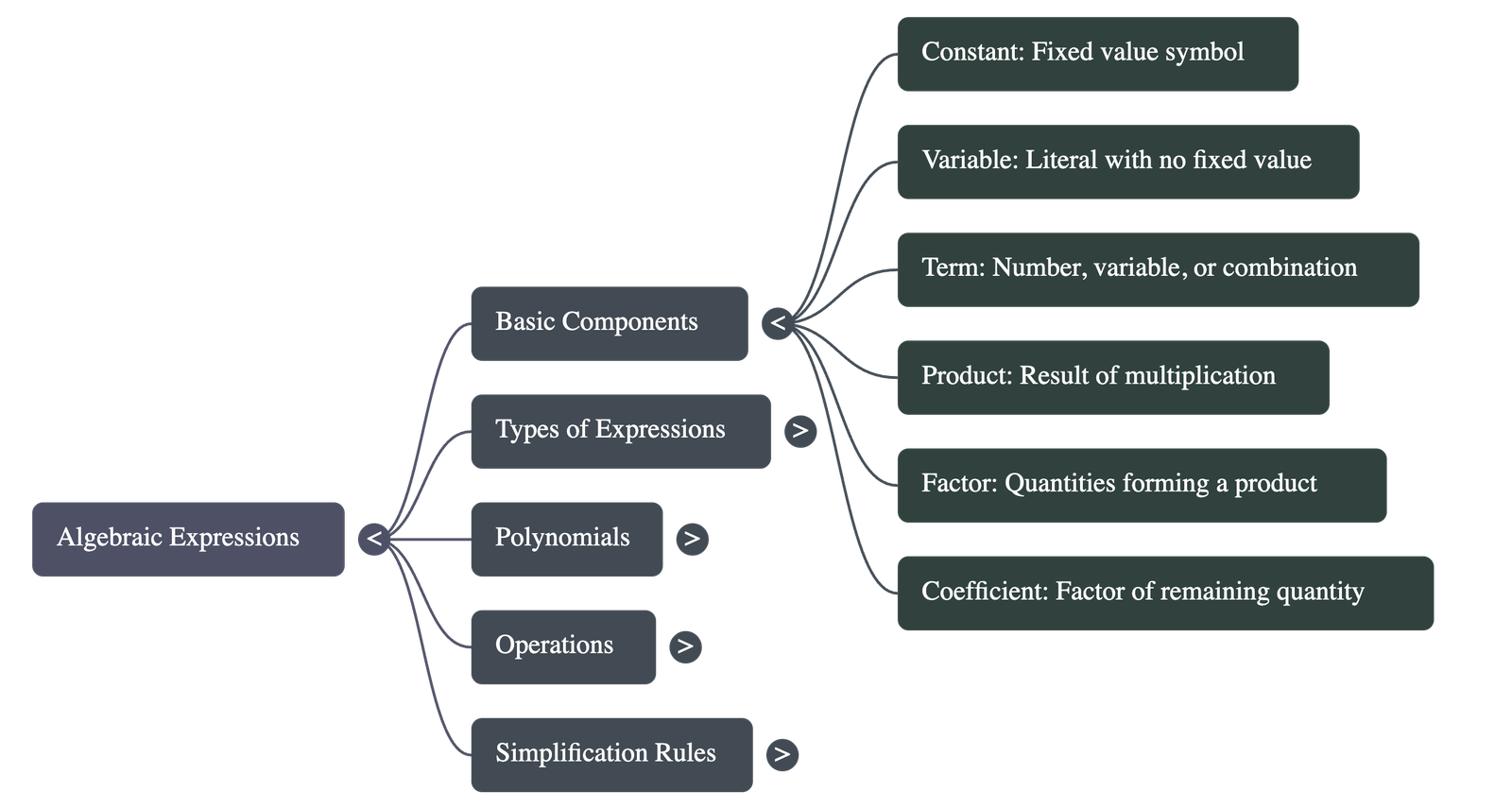
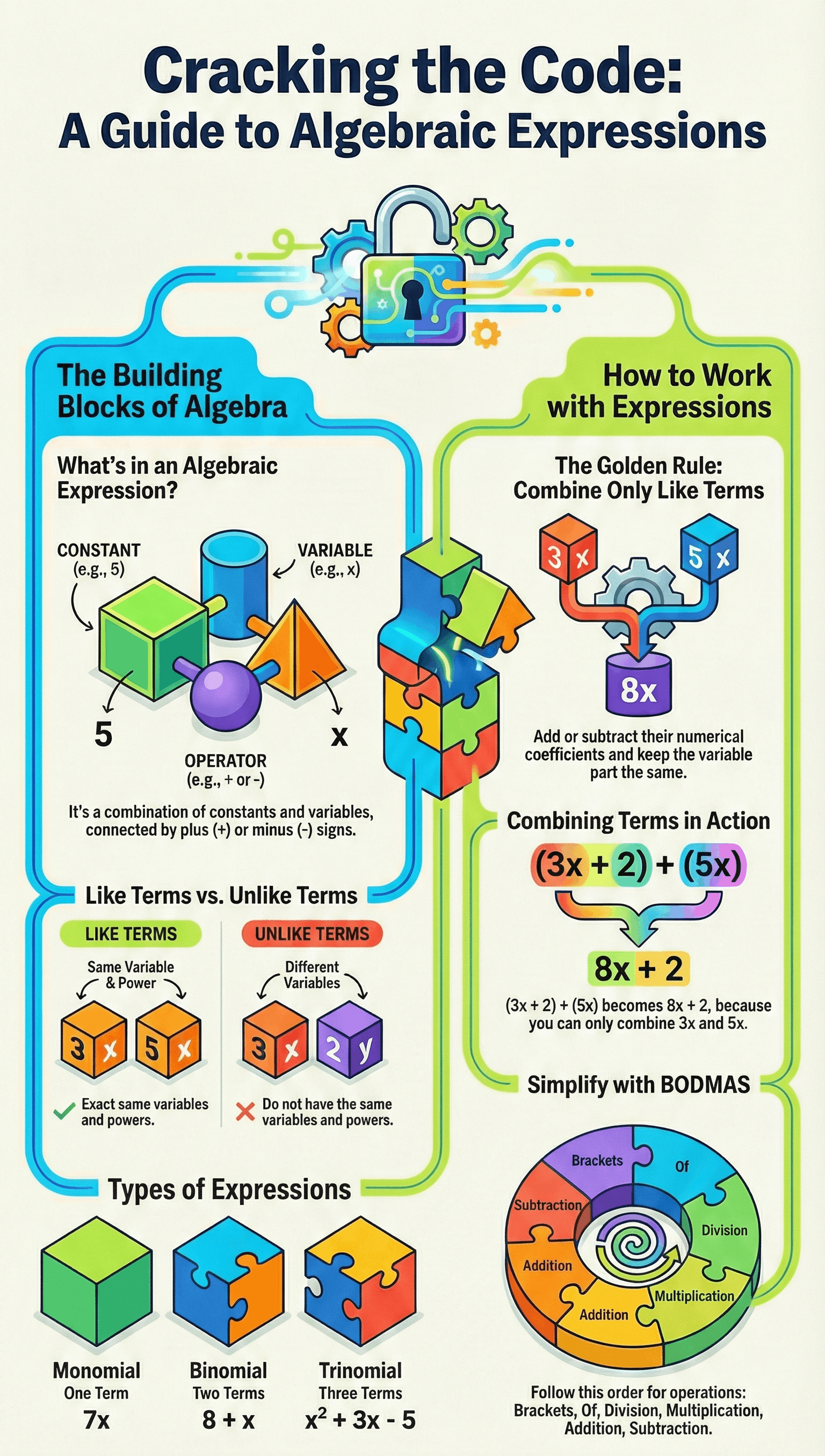
• Constants: Symbols that have a fixed numerical value (e.g., 8, -15, √3).
• Variables (Literals): Symbols that do not have a fixed value and can be assigned various values based on requirements (e.g., x, y, z).
• Terms: A number, a variable, or a combination of them in the form of a product or quotient (e.g., 7x, 3xy, -6/x).

2. Types of Algebraic Expressions

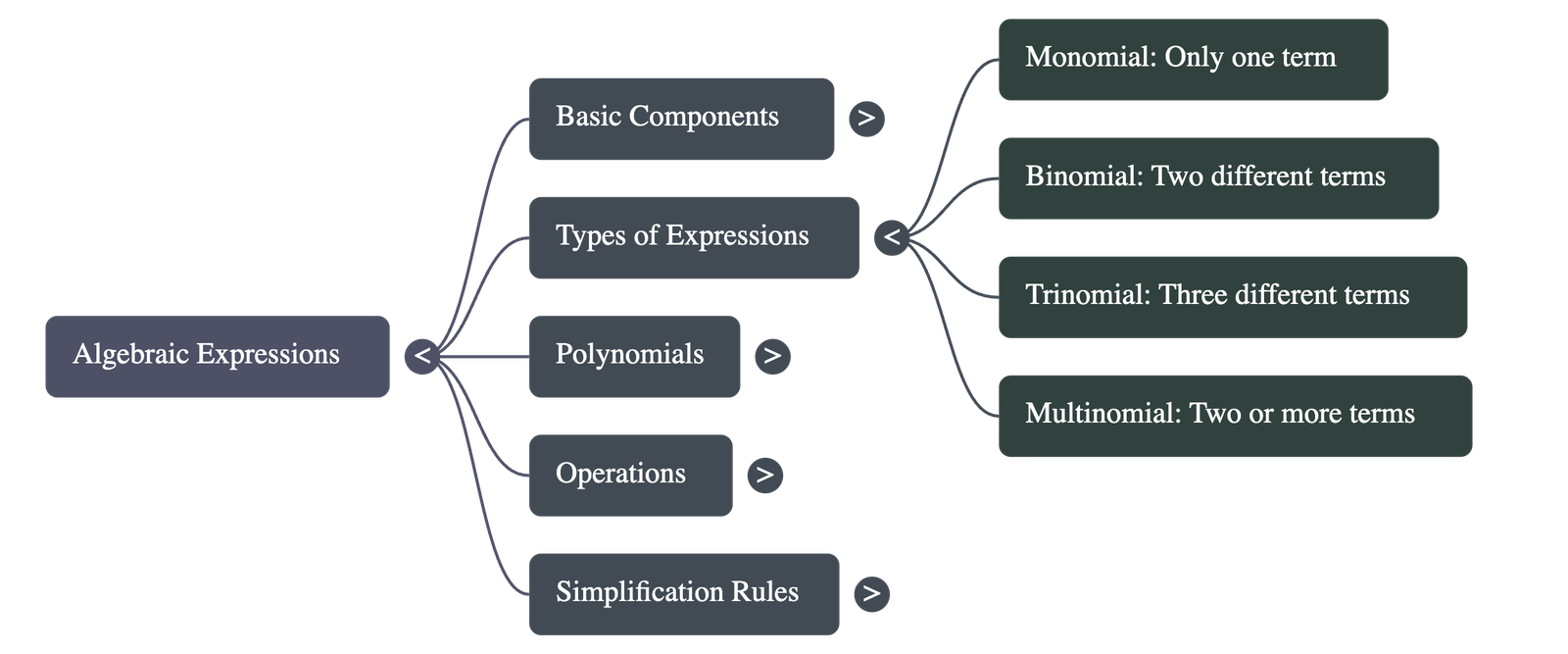
• Algebraic Expression: A collection of terms connected by addition (+) or subtraction (-) signs.
• Monomial: An expression containing only one term.
• Binomial: An expression containing exactly two different terms.
• Trinomial: An expression containing exactly three different terms.
• Multinomial: An expression containing two or more terms. Every binomial and trinomial is also a multinomial.

3. Concept of Polynomials

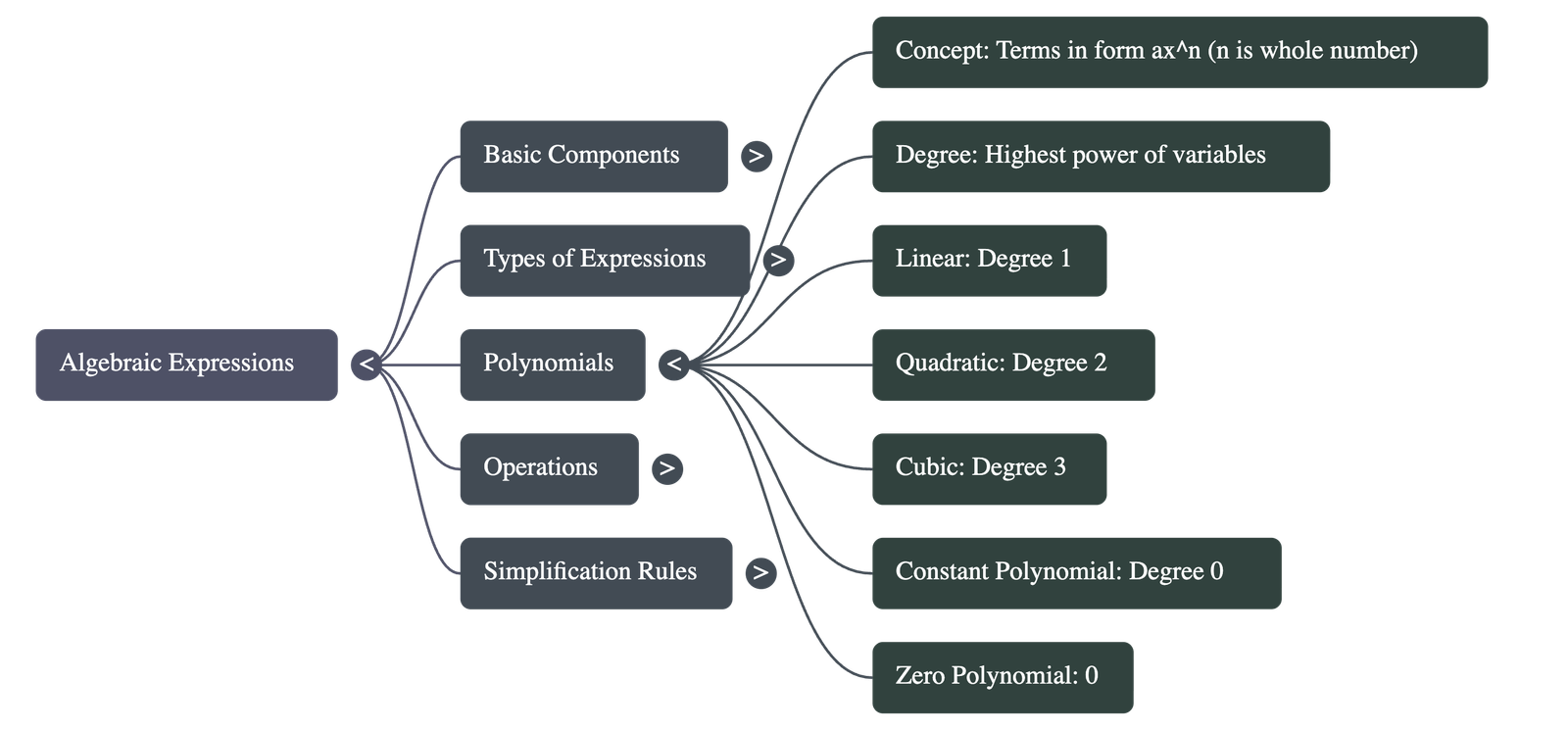
• Definition: An algebraic expression where each term follows the form axⁿ, and n must be a whole number. If the exponent is negative or a fraction, it is not a polynomial.
• Degree of a Polynomial:
  • For a single variable, it is the highest power of that variable.
  • For multiple variables, it is the highest sum of the powers of variables in any single term.
• Classification by Degree:
  • Linear: Degree 1
  • Quadratic: Degree 2
  • Cubic: Degree 3
  • Constant: Degree 0

4. Factors and Coefficients

• Factors: Each quantity (constant or variable) that is multiplied to form a product. The constant part is the numeral factor, and the variable part is the literal factor.
• Coefficients: Any factor of a term is called the coefficient of the remaining part of that term.
• Like Terms: Terms that have the exact same literal coefficients (variables and powers). Only like terms can be added or subtracted.

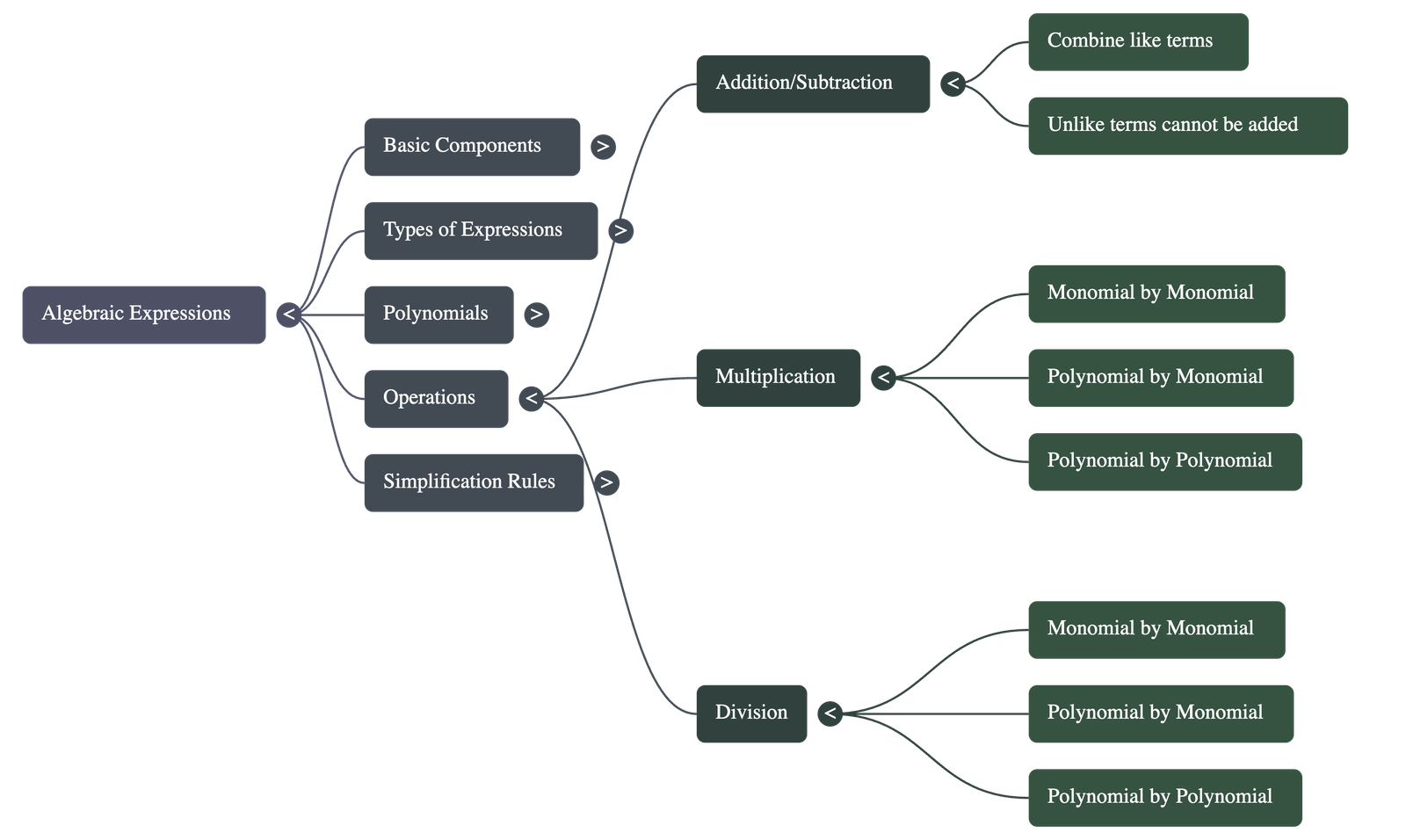
5. Basic Operations

• Addition & Subtraction: Performed by combining the numerical coefficients of like terms. Unlike terms must be kept separate.
• Multiplication:
  • When multiplying literals, powers are added: x^m × xⁿ = x^m+n.
  • Polynomial multiplication involves multiplying each term of one expression by every term of the other.
• Division:
  • When dividing literals, powers are subtracted: x^m ÷ xⁿ = x^m-n.
  • The relationship holds: Dividend = (Quotient × Divisor) + Remainder.

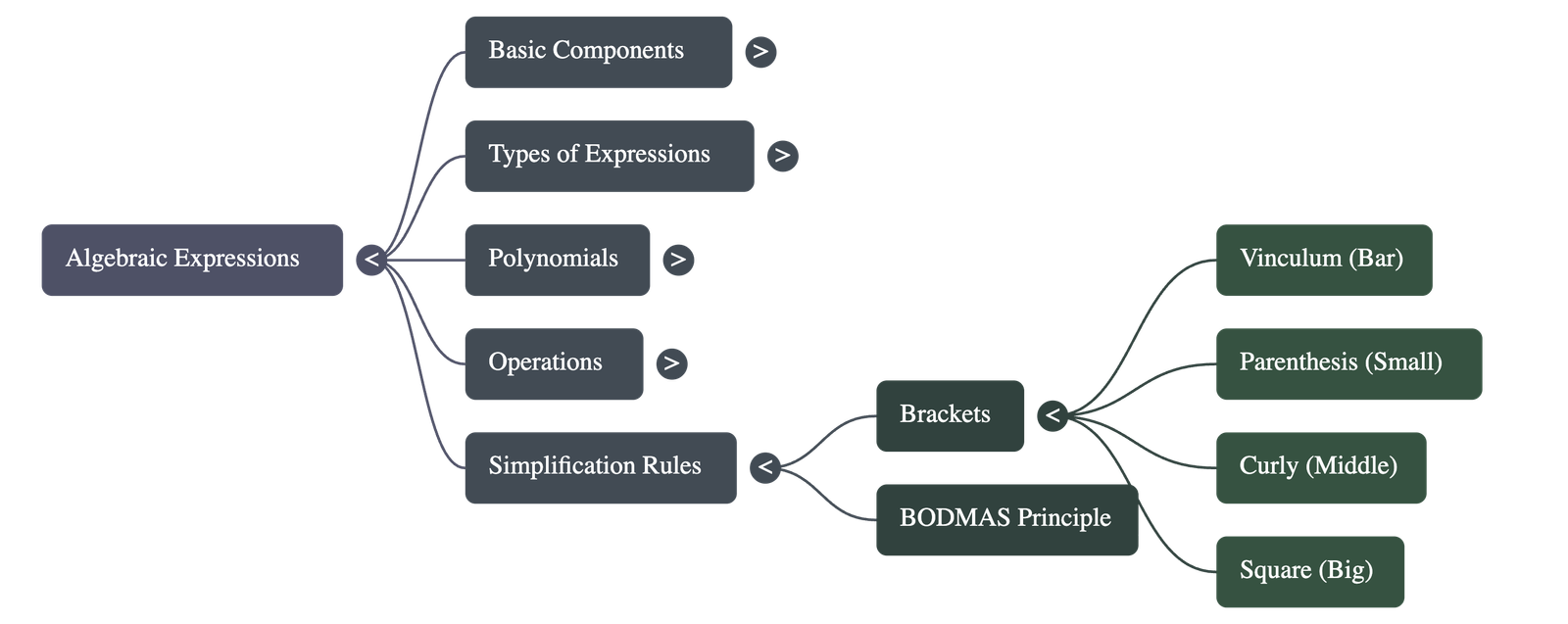
6. Simplification and BODMAS

• Brackets: Operations must follow a specific order of removal: 1. Vinculum (bar), 2. Parenthesis (round), 3. Curly brackets, 4. Square brackets.
• BODMAS Principle: The order of operations is Brackets, Of, Division, Multiplication, Addition, and Subtraction.