Understanding Shapes (Including Polygons)

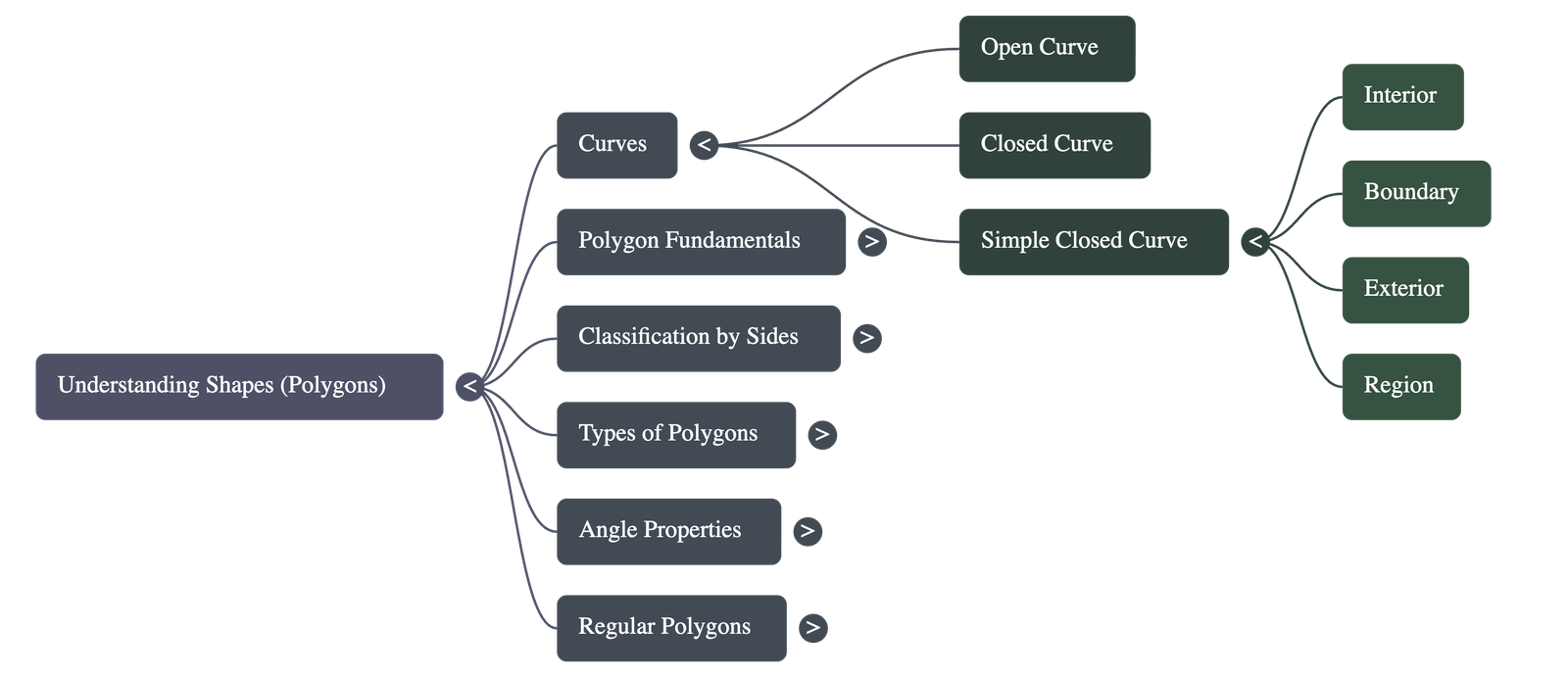
1. Introduction to Curves

• Mathematical Definition: In geometry, even a straight line is considered a curve.
• Open Curve: A curve that does not cut itself.
• Closed Curve: A curve that cuts itself to enclose a space.
• Simple Closed Curve: A closed curve that does not pass through any of its points more than once.
• Regions: A simple closed curve divides a plane into three parts: the interior, the boundary, and the exterior. The interior combined with the boundary is known as the region.

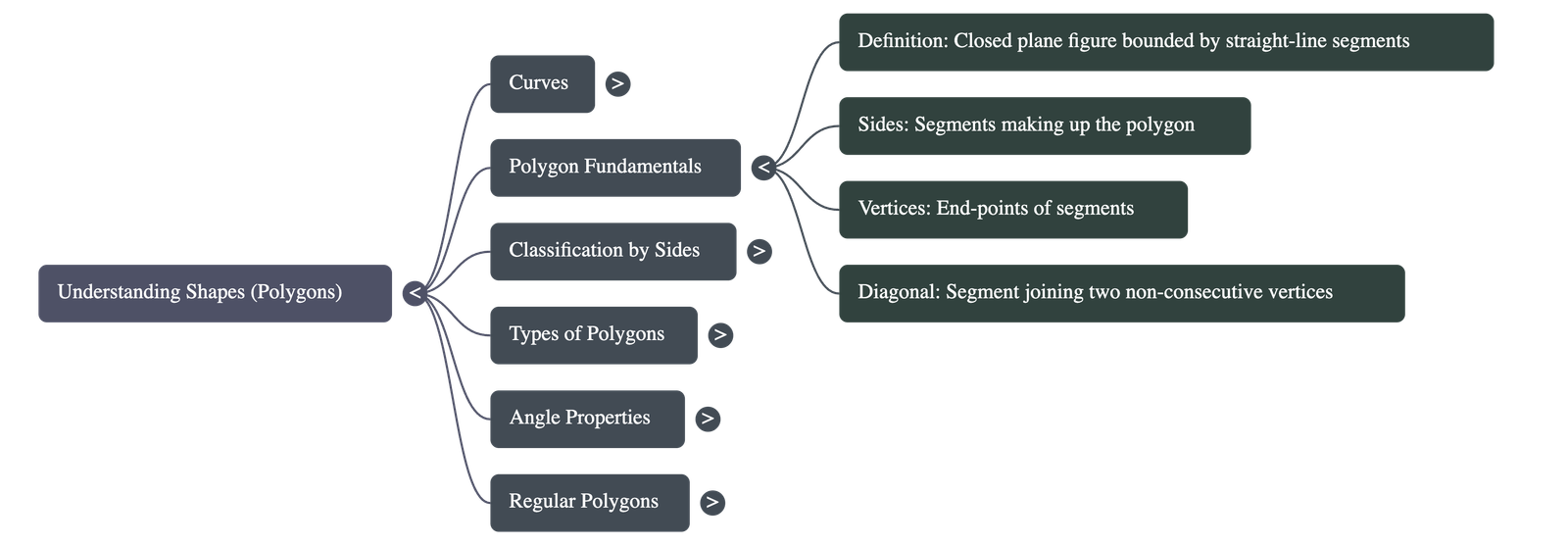
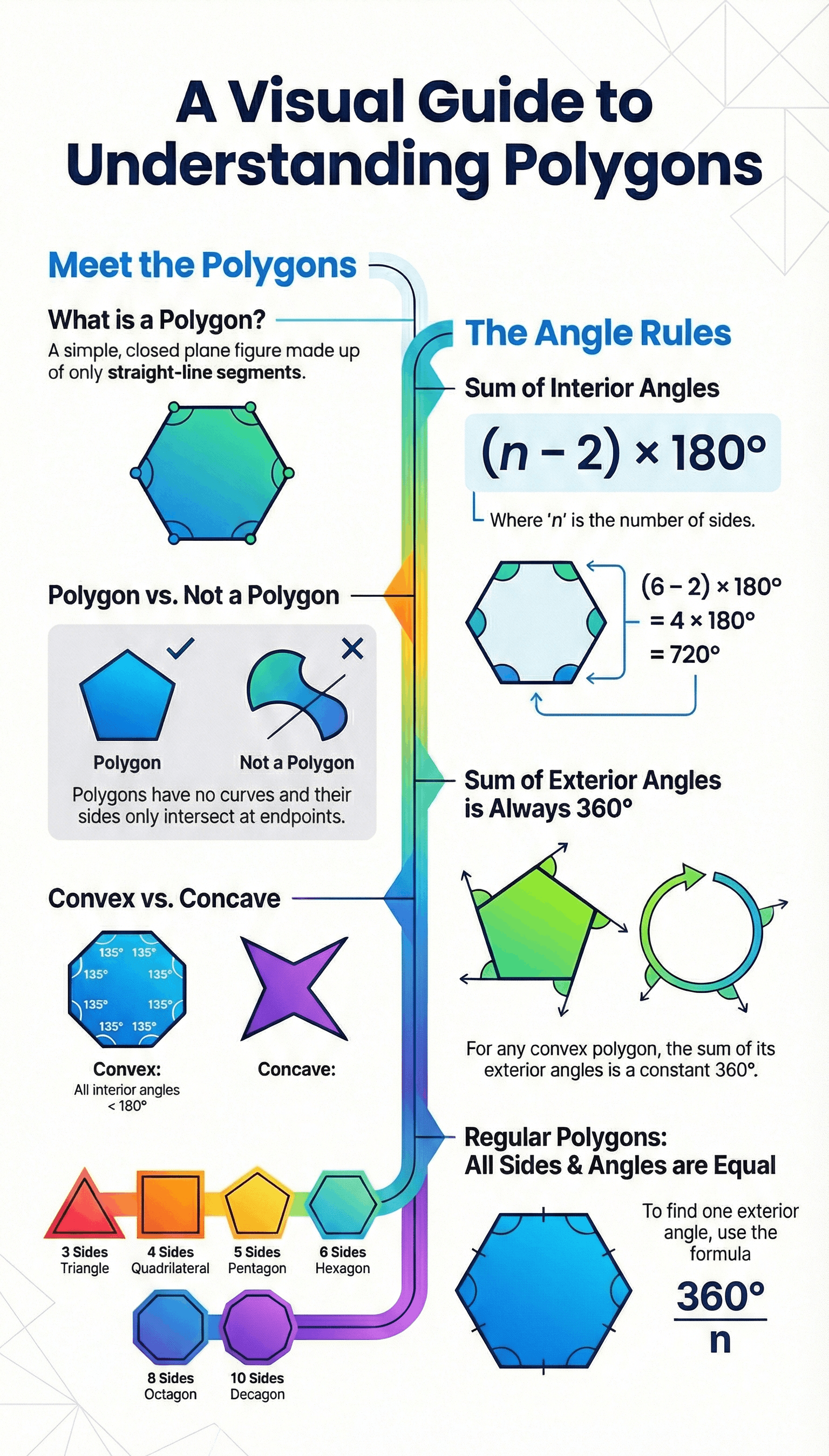
2. Polygons and Their Classification

• Definition: A polygon is a closed plane figure bounded by straight-line segments. The segments must intersect only at their endpoints, and each endpoint must be shared by exactly two segments.
• Components: The segments forming the polygon are sides, and their endpoints are vertices.
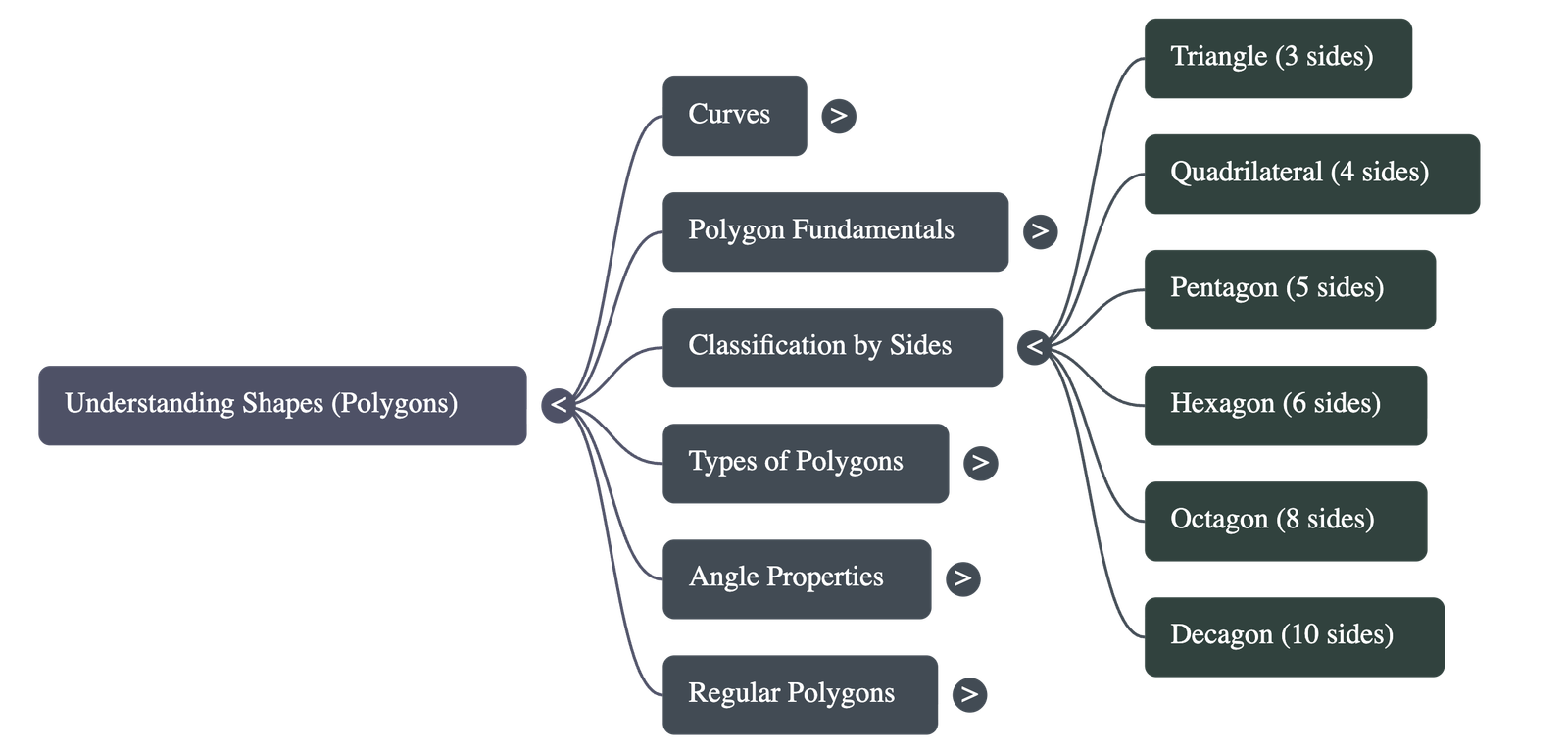
• Naming Conventions: Polygons are named based on their number of sides:
  • 3 Sides: Triangle
  • 4 Sides: Quadrilateral
  • 5 Sides: Pentagon
  • 6 Sides: Hexagon
  • 8 Sides: Octagon
  • 10 Sides: Decagon
• Diagonal: A line segment joining any two non-consecutive vertices.

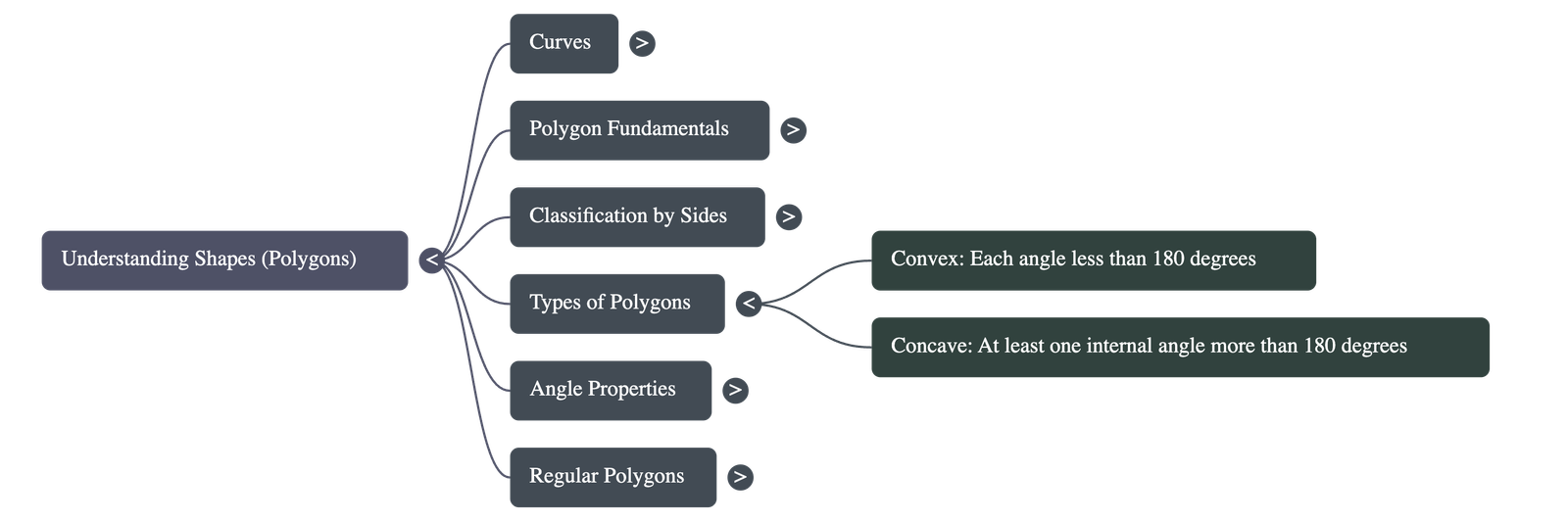
3. Types of Polygons

• Convex Polygon: A polygon where every internal angle is less than 180°. (Unless stated otherwise, "polygon" usually refers to a convex one).
• Concave (Re-entrant) Polygon: A polygon where at least one internal angle is more than 180°.

4. Key Angle Formulas

• Sum of Interior Angles: For a polygon with n sides, the sum is calculated as:
  (n - 2) × 180°   OR   (2n - 4) right angles
• Sum of Exterior Angles: If the sides are produced in order, the sum of all exterior angles is always 360° (4 right angles), regardless of the number of sides.
• Side Constraints: The number of sides in a polygon must be a natural number and cannot be less than 3.

5. Regular Polygons

• Definition: A polygon is "regular" if all its interior angles are equal, all its sides are equal, and all its exterior angles are equal.
• Individual Angle Formulas: For a regular polygon with n sides:
  • Each Interior Angle: [(2n - 4) × 90°] / n
  • Each Exterior Angle: 360° / n
• Calculating Sides: If the exterior angle is known, the number of sides n is:
  n = 360° / Exterior Angle
• The Linear Pair Property: At any vertex of a polygon, the Interior Angle + Exterior Angle = 180°, as they form a straight line.