Chapter 14: Linear Equations in One Variable

1. Fundamentals of Equations

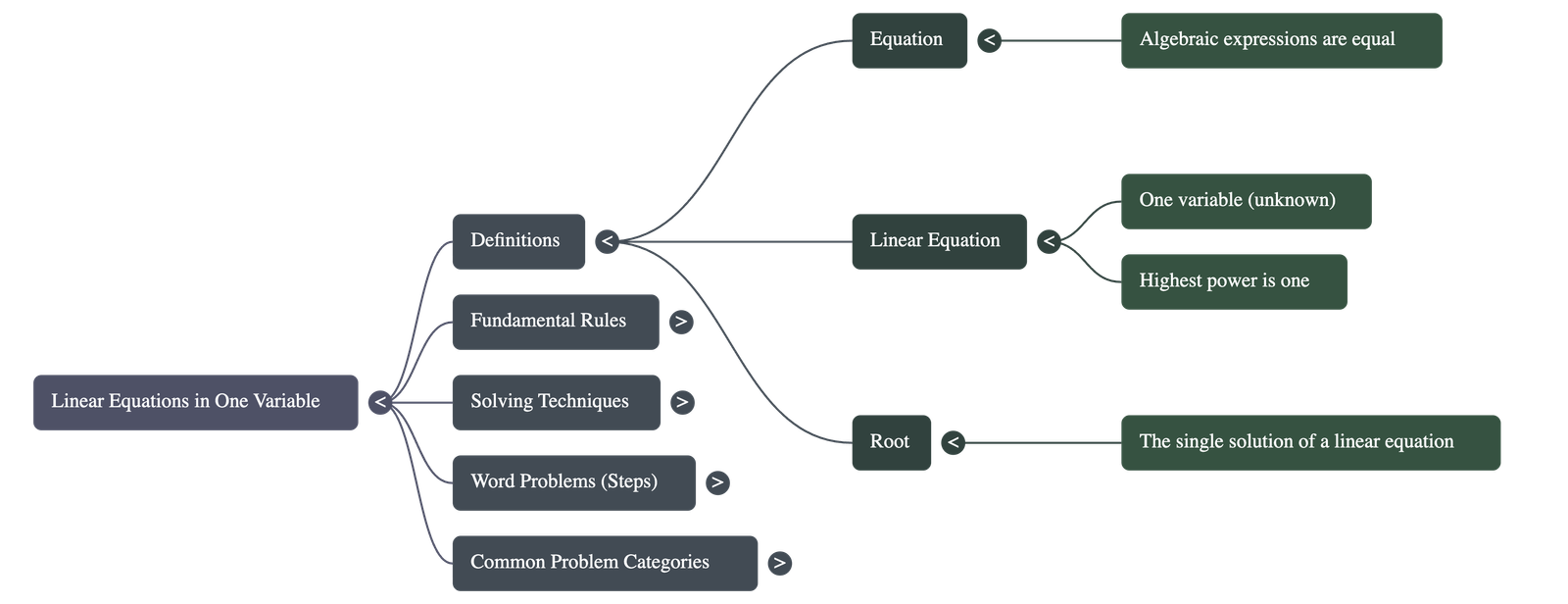
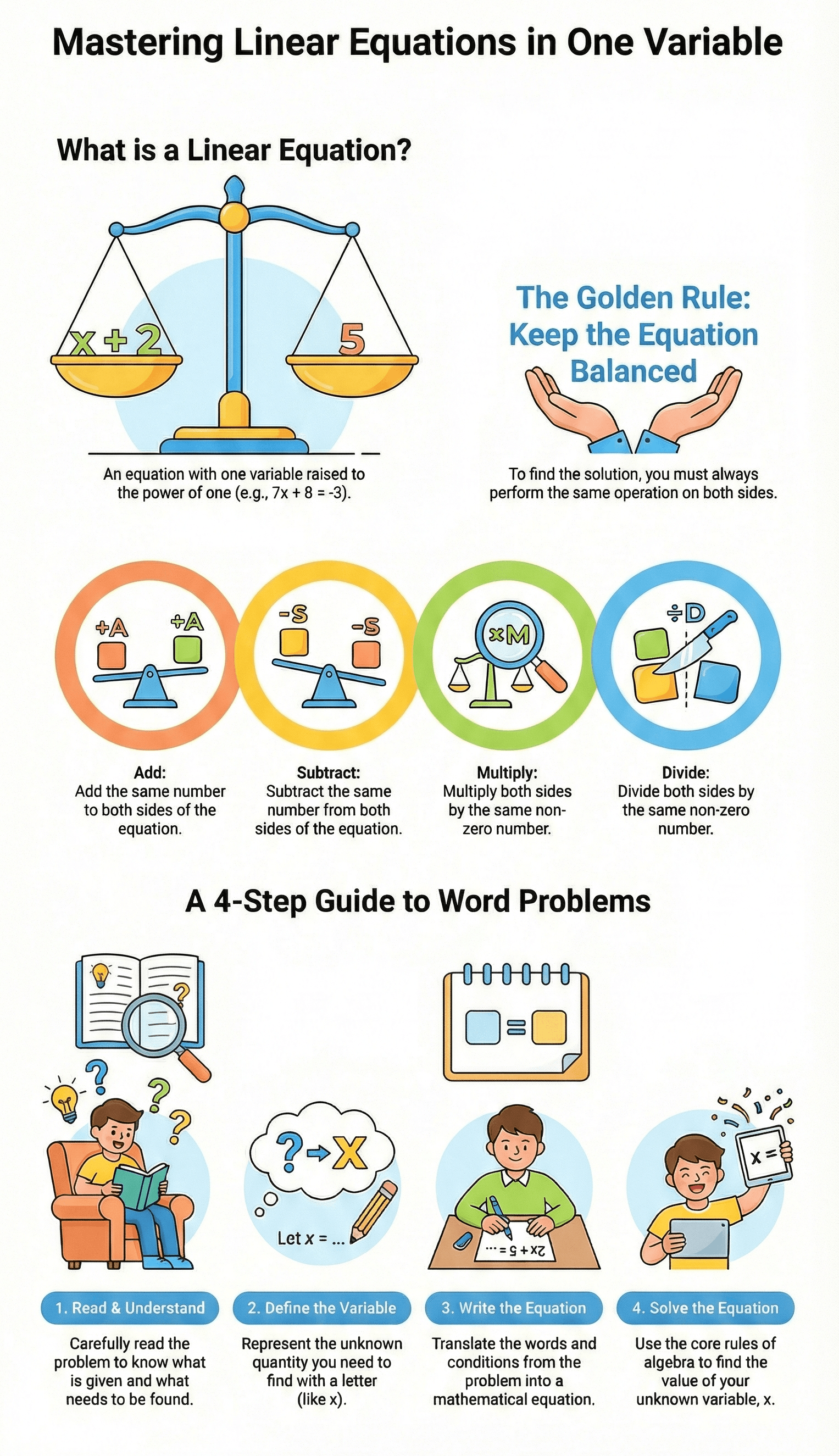
• Definition of an Equation: A statement asserting that two algebraic expressions are equal.
• Linear Equation in One Variable: An equation involving only one unknown variable where the highest power of that variable is one.
• The Root: A linear equation has exactly one solution, which is formally referred to as its root.

2. Rules for Maintaining Equation Equality

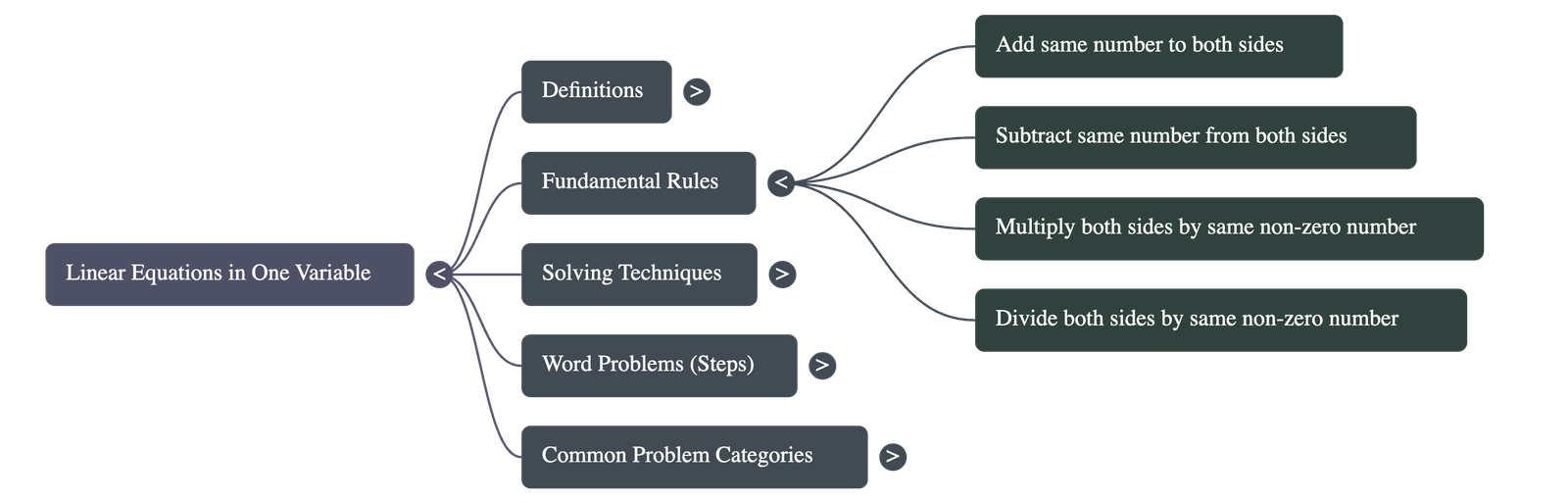
An equation remains unchanged and balanced when the following operations are applied to both sides:

• Adding the same number.
• Subtracting the same number.
• Multiplying by the same non-zero number.
• Dividing by the same non-zero number.

3. Methods for Solving Equations

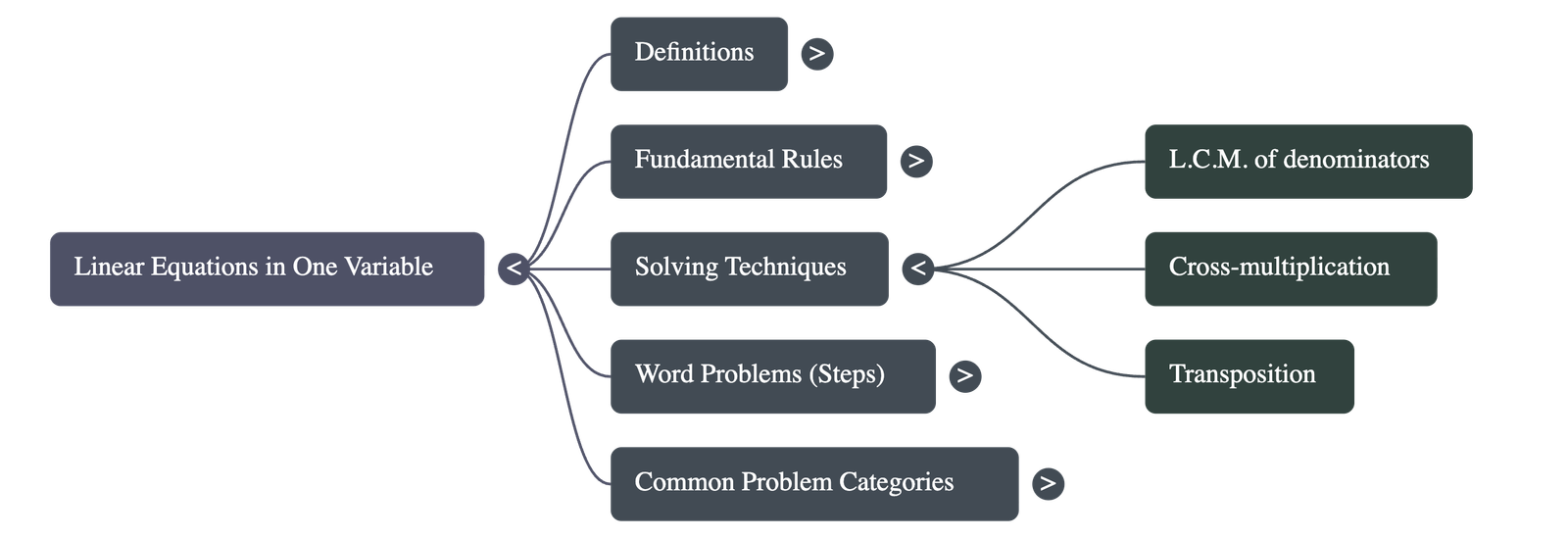
• Transposition: Moving terms from one side to the other by changing their signs.
• Cross-Multiplication: Used when equations are in a fractional format (e.g., a/b = c/d) to eliminate denominators.
• LCM Method: When dealing with multiple denominators, multiplying every term by the Least Common Multiple (LCM) of the denominators simplifies the equation into a linear form.

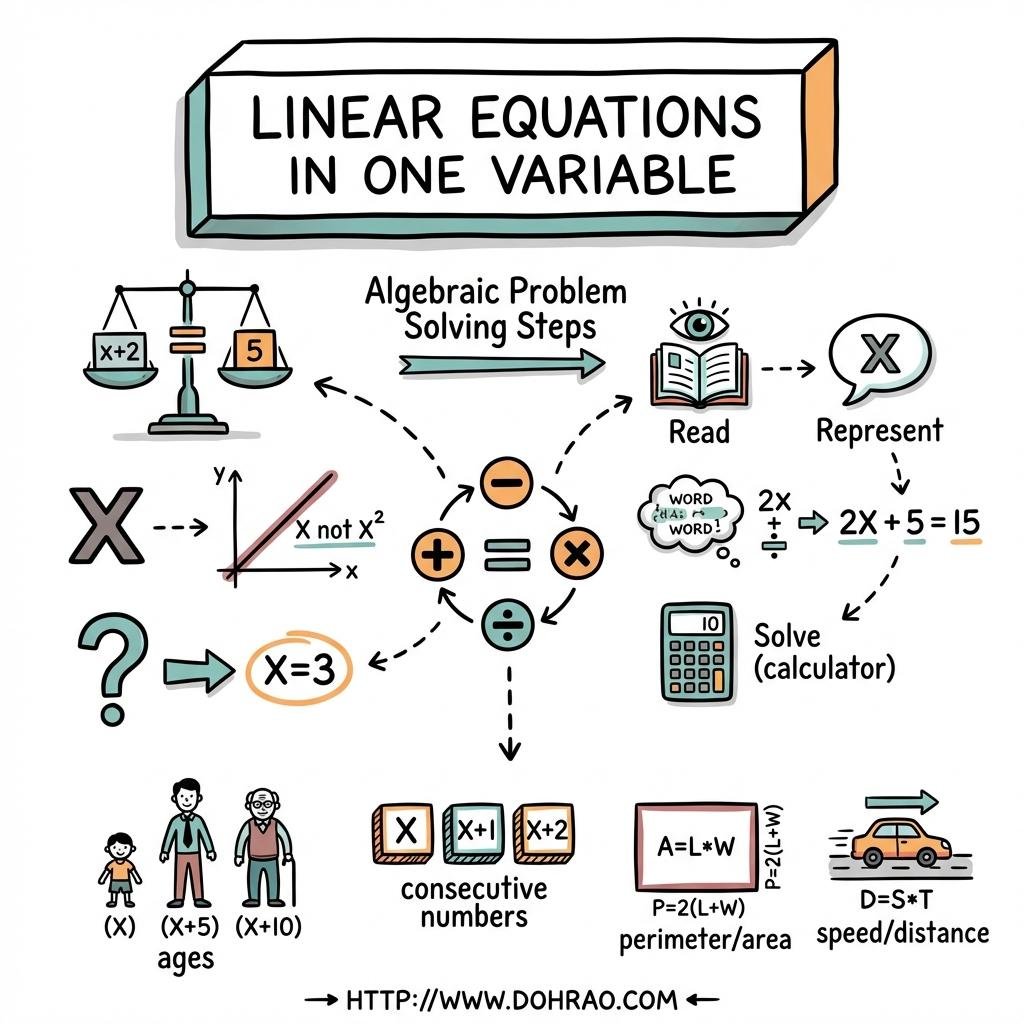
4. Strategies for Word Problems

Solving real-world problems involves a systematic four-step process:

1. Analysis: Read the problem carefully to identify what is given and what needs to be found.
2. Variable Assignment: Represent the unknown quantity using a letter (typically x, y, or a).
3. Formulation: Write a mathematical relation (equation) based on the conditions provided in the problem.
4. Resolution: Solve the equation to find the value of the unknown.

5. Common Problem Categories

• Number Systems:
  • Consecutive integers: x, x+1, x+2...
  • Consecutive even or odd numbers: x, x+2, x+4...
  • Consecutive multiples (e.g., of 3): x, x+3, x+6...
• Geometry: Problems involving the perimeter and dimensions (length and width) of shapes like rectangles.
• Age Problems: Comparing ages at different points in time (e.g., "five years ago" or "ten years hence").
• Kinematics: Using the relationship Time = Distance / Speed to find unknown distances or times.
• Practical Applications: Solving for fractions, ratios, and monetary calculations involving wages and fines.