Quick Navigation:
| | |
Quadratic Equations
1. Introduction and Historical Background
- Quadratic equations arise frequently in real-life situations, such as calculating dimensions of a room given its area and a relationship between length and breadth.
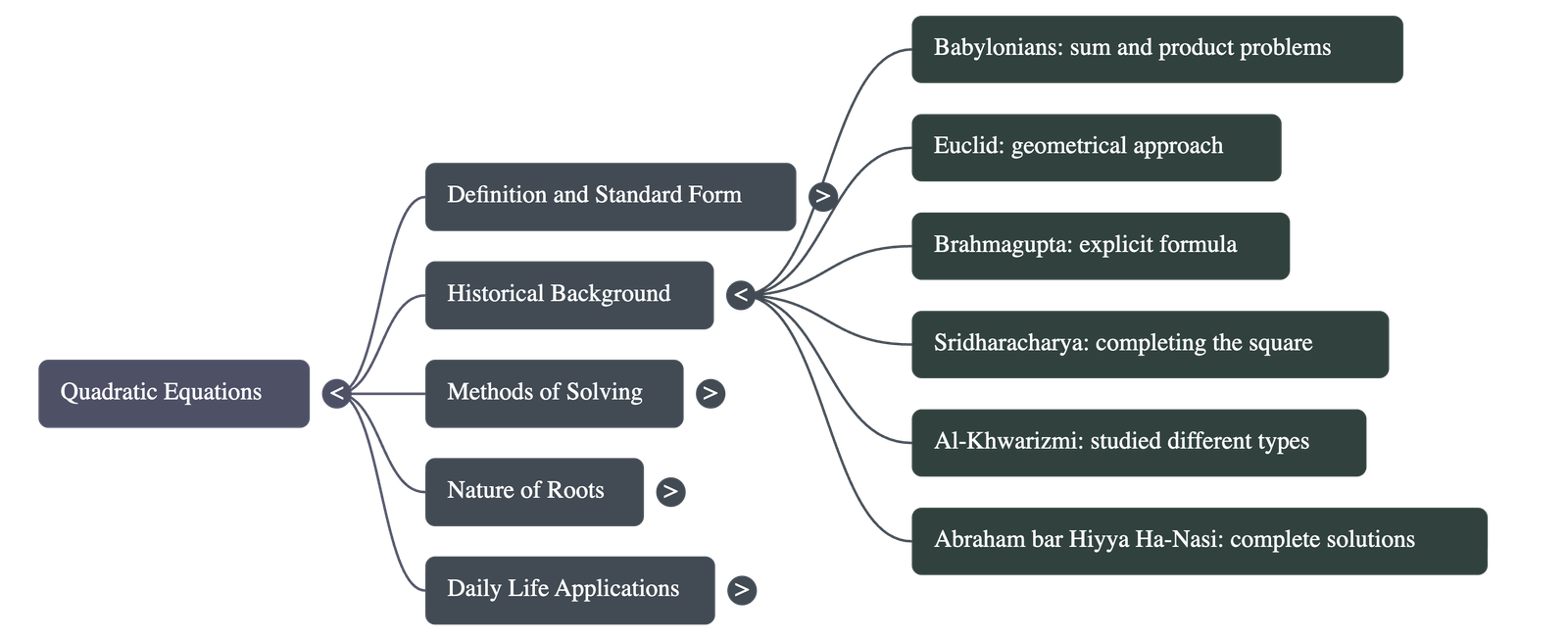
- Babylonians were likely the first to solve quadratic equations (finding two numbers with a given sum and product).
- Euclid developed a geometrical approach to finding lengths that correspond to solutions of quadratic equations.
- Brahmagupta (C.E. 598–665) provided an explicit formula to solve equations of the form ax2 + bx = c.
- Sridharacharya (C.E. 1025) derived the quadratic formula using the method of completing the square.
- Al-Khwarizmi (approx. C.E. 800) and Abraham bar Hiyya Ha-Nasi also contributed significantly to the study of these equations.
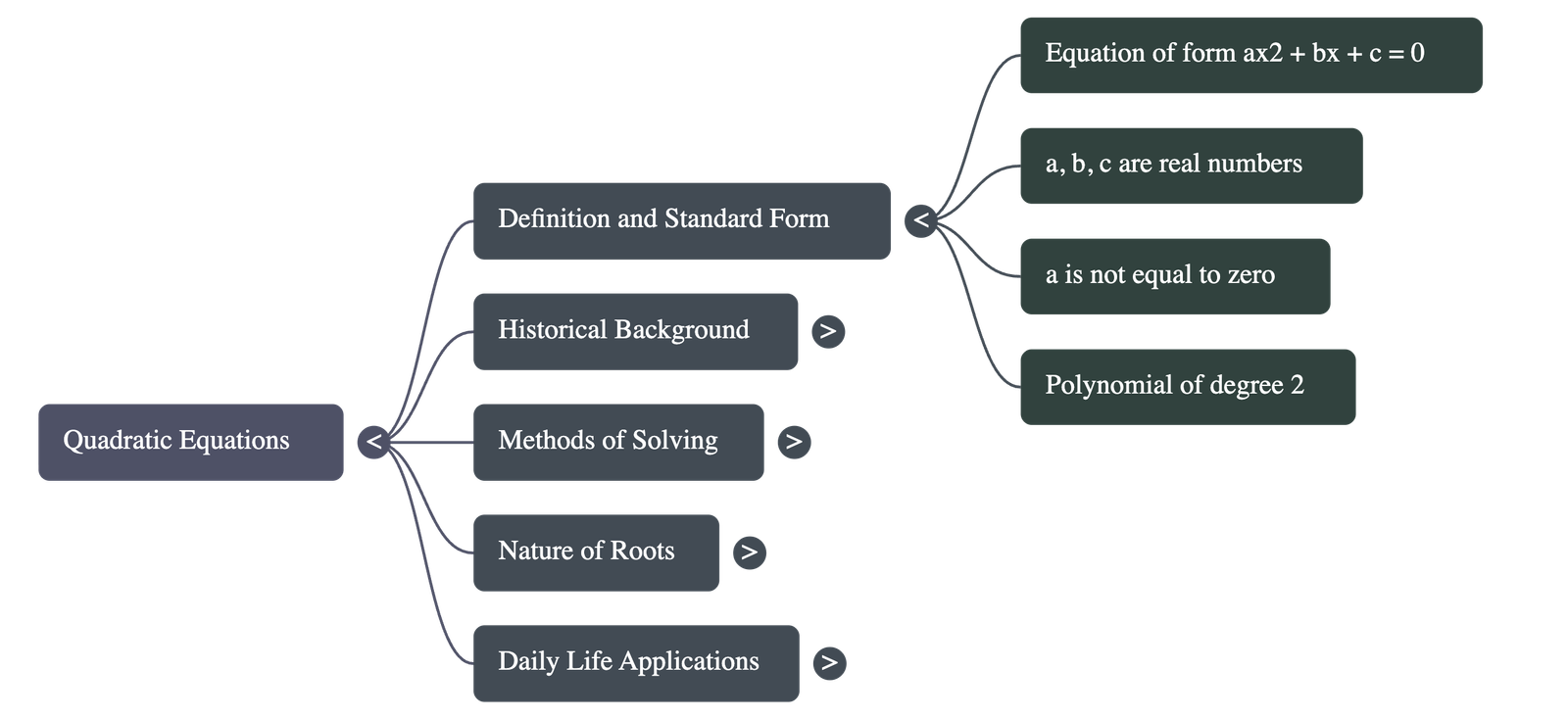
2. Definition of a Quadratic Equation
- A quadratic equation in the variable x is an equation of the form:
ax2 + bx + c = 0where a, b, and c are real numbers and a ≠ 0.
- Any equation of the form p(x) = 0, where p(x) is a polynomial of degree 2, is a quadratic equation.
- Writing the terms in descending order of their degrees yields the standard form of the equation.
- Equations may sometimes appear cubic or linear initially but simplify into quadratic equations (e.g., (x + 1)2 = 2(x - 3)).
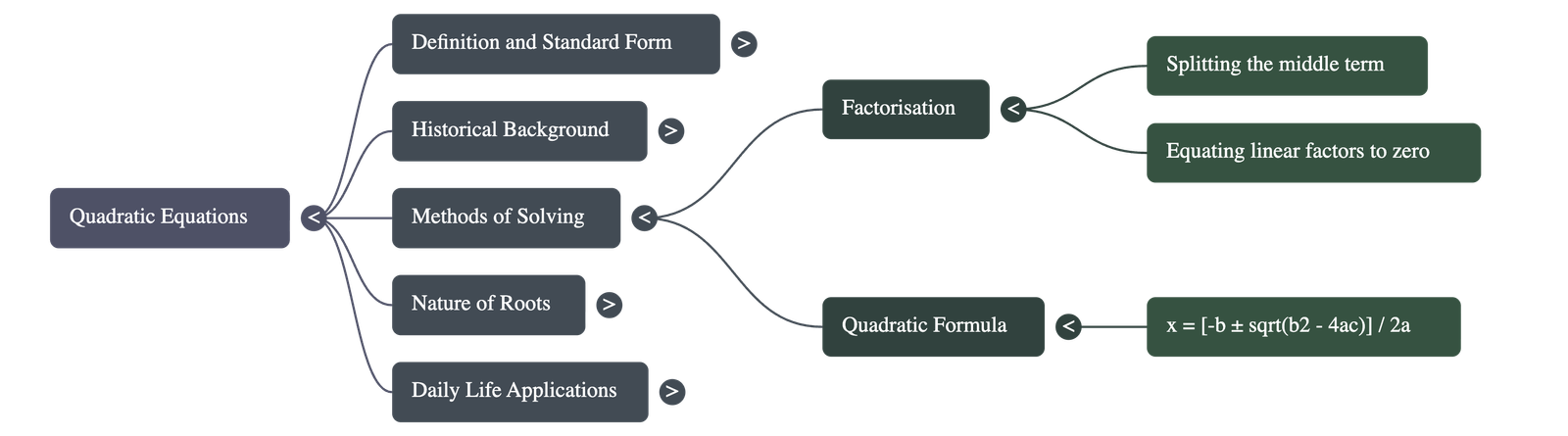
3. Solution by Factorisation
- A real number α is called a root of the quadratic equation ax2 + bx + c = 0 if aα2 + bα + c = 0.
- The roots of the quadratic equation are identical to the zeroes of the corresponding quadratic polynomial.
- A quadratic equation can have at most two roots.
- Method:
- Split the middle term bx into two parts such that their product equals the product of ax2 and c.
- Factorise the equation into two linear factors.
- Equate each factor to zero to find the values of x.
- Example: To solve 2x2 - 5x + 3 = 0, split -5x into -2x and -3x, factorise to get (2x - 3)(x - 1) = 0, yielding roots 3/2 and 1.
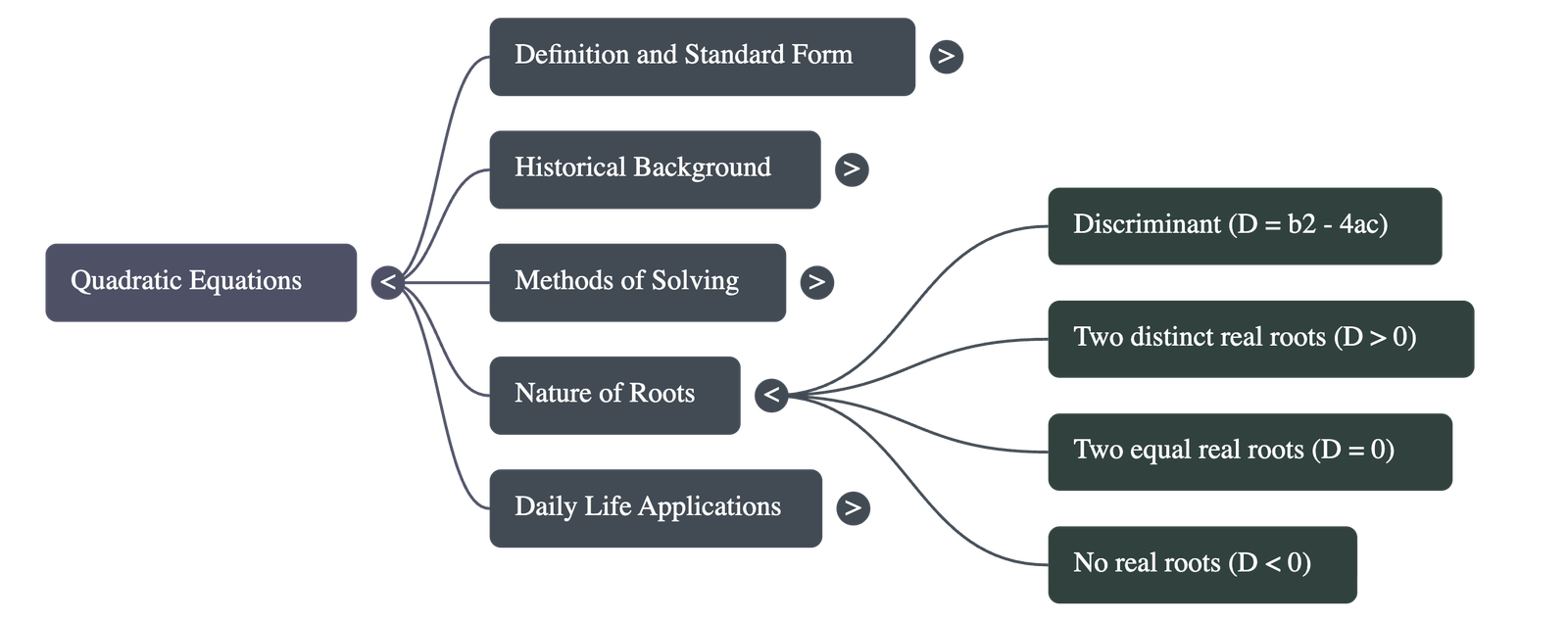
4. Nature of Roots and Discriminant
- The roots of ax2 + bx + c = 0 can be calculated using the quadratic formula:
x = -b ± √(b2 - 4ac) 2a
- The term b2 - 4ac is known as the discriminant of the quadratic equation. It determines the nature of the roots.
- There are three cases for the nature of roots:
- Two distinct real roots: If b2 - 4ac > 0.
- Two equal real roots (Coincident roots): If b2 - 4ac = 0. (In this case, x = -b/2a).
- No real roots: If b2 - 4ac < 0 (the square root of a negative number is not real).
5. Applications
- Quadratic equations are used to solve word problems involving areas, perimeters, and numbers.
- When solving real-world problems (like length or time), negative roots are often ignored if they do not make physical sense in the context of the problem.
Quick Navigation:
| | |
1 / 1
Quick Navigation:
| | |