Polynomials

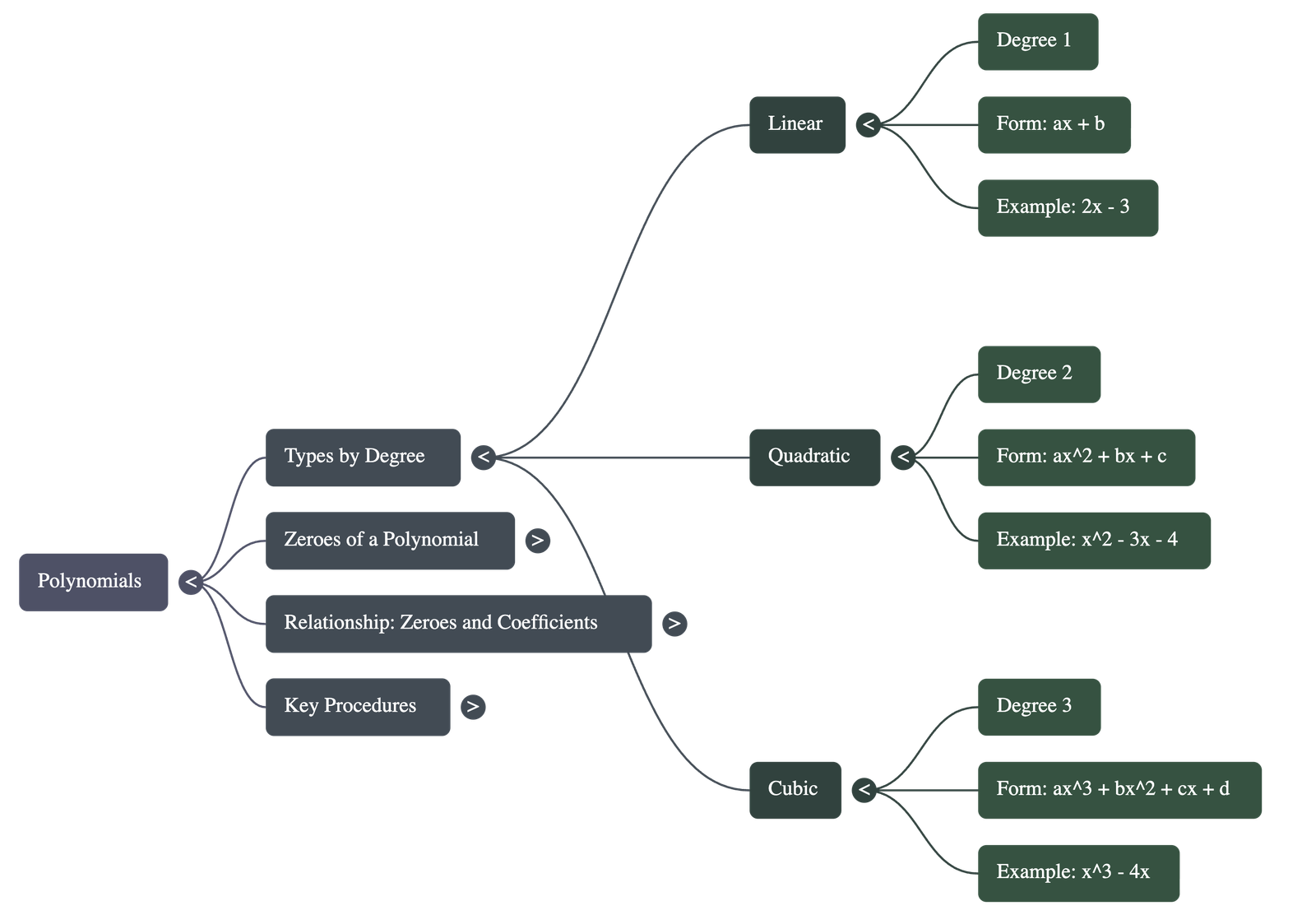
1. Introduction to Polynomials

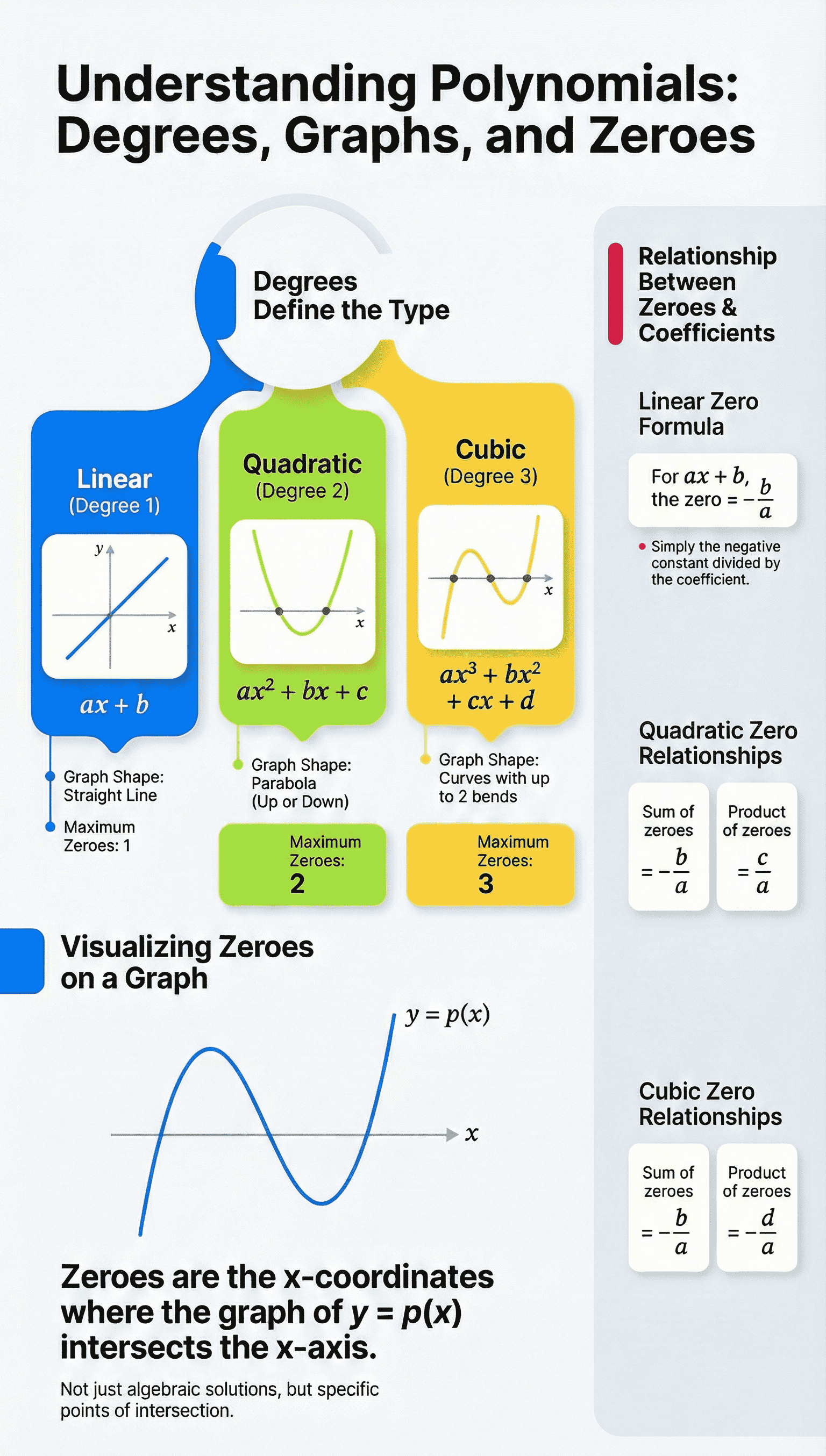
• Definition: If p(x) is a polynomial in x, the highest power of x in p(x) is called the degree of the polynomial.
• Linear Polynomial: A polynomial of degree 1.
  (General form: ax + b, where a ≠ 0)
• Quadratic Polynomial: A polynomial of degree 2. The word 'quadratic' comes from 'quadrate', meaning square.
  (General form: ax² + bx + c, where a ≠ 0)
• Cubic Polynomial: A polynomial of degree 3.
  (General form: ax³ + bx² + cx + d, where a ≠ 0)

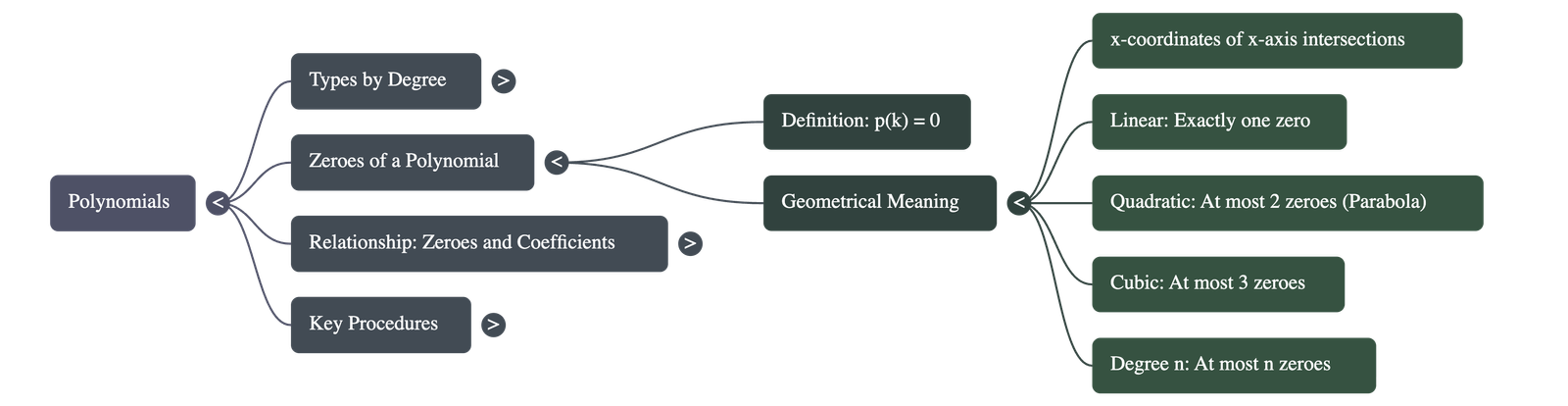
2. Zeroes of a Polynomial

A real number k is said to be a zero of a polynomial p(x) if p(k) = 0.

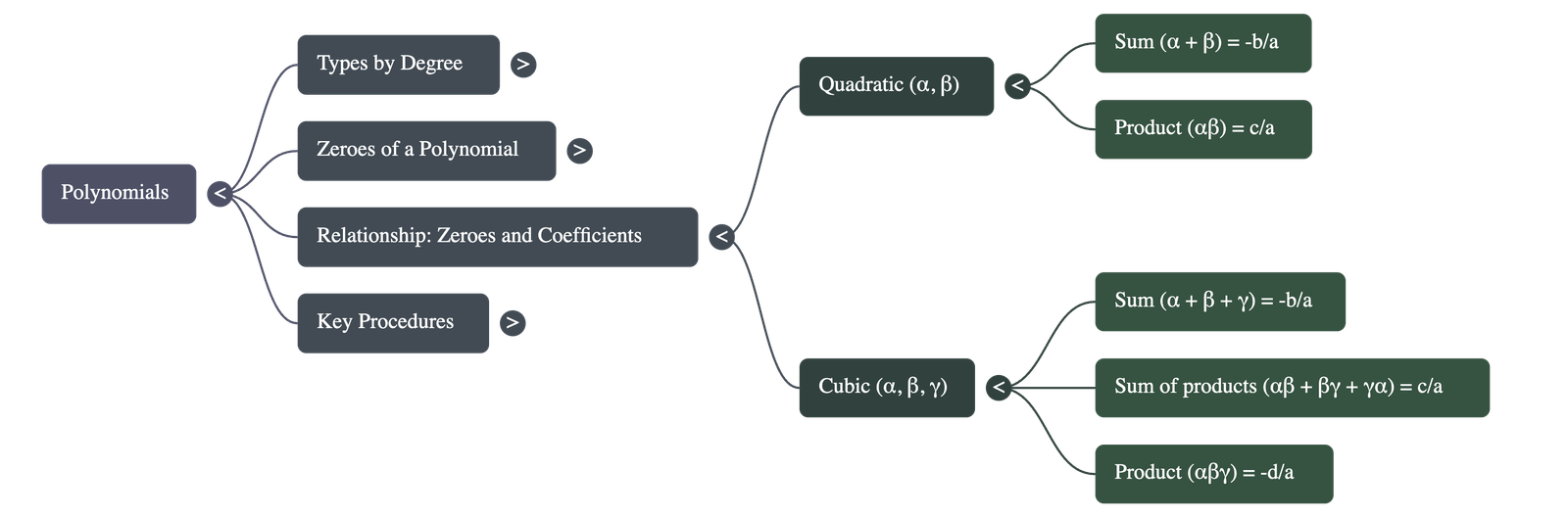
• For a linear polynomial ax + b, the zero is -b/a.
• The zero of a linear polynomial is related to its coefficients:
  Zero = -(Constant term) / (Coefficient of x).

3. Geometrical Meaning of Zeroes

The zeroes of a polynomial p(x) are geometrically the x-coordinates of the points where the graph of y = p(x) intersects the x-axis.

Linear Polynomials

• The graph of y = ax + b is a straight line.
• It intersects the x-axis at exactly one point.
• A linear polynomial has exactly one zero.

Quadratic Polynomials (Parabolas)

• The graph of y = ax² + bx + c is a curve called a parabola.
• It opens upwards if a > 0 and downwards if a < 0.
• The graph can intersect the x-axis in three ways:
  1. Two distinct points: The polynomial has two distinct zeroes.
  2. One point (touching): The two points coincide; the polynomial has two equal zeroes (effectively one zero).
  3. No points: The graph is strictly above or below the x-axis; the polynomial has no real zeroes.
• Conclusion: A quadratic polynomial has at most 2 zeroes.

Cubic Polynomials

• The graph can intersect the x-axis at most at 3 points.
• A cubic polynomial has at most 3 zeroes.
• General Rule: A polynomial p(x) of degree n has at most n zeroes.