Surface Areas and Volumes

1. Introduction

• The chapter builds upon previous knowledge of basic solids: cuboids, cones, cylinders, and spheres.
• Real-world objects are often combinations of these standard shapes. Examples include:
  • A truck container made of a cylinder with hemispheres at both ends.
  • A test tube made of a cylinder and a hemisphere.
  • Buildings and monuments constructed from various geometric forms.
• The primary goal of this chapter is to learn how to calculate the surface areas and volumes of these complex, combined solids.

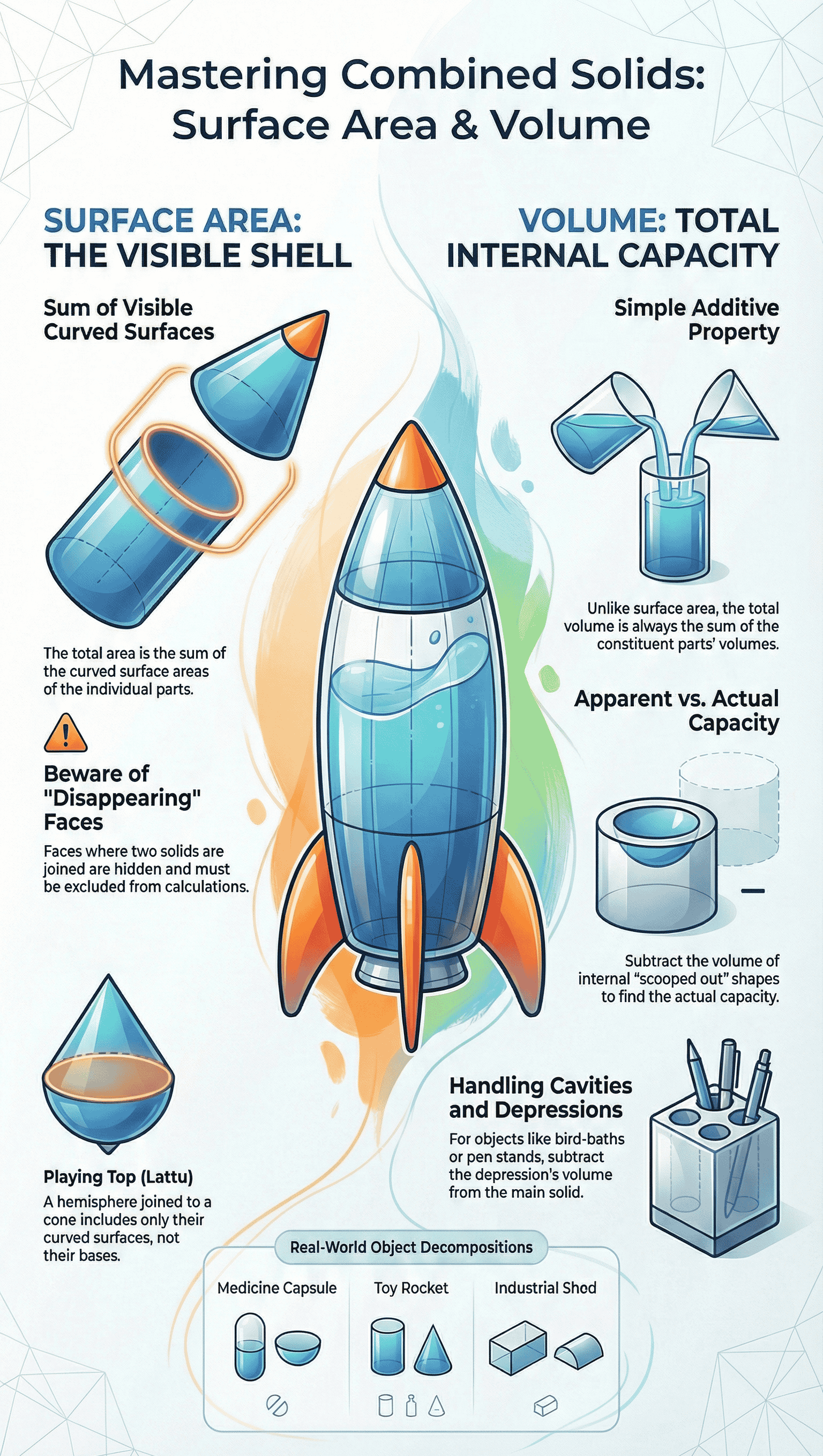
2. Surface Area of a Combination of Solids

When calculating the surface area of a combined solid, the problem is broken down into simpler, known geometric parts.

• Key Concept: The total surface area of a new solid is the sum of the curved surface areas (CSA) of the individual parts that are visible.
• Methodology:
  • Identify the individual solids that make up the object.
  • Visualize which surfaces are exposed and which are hidden (joined together).
  • Add the areas of the exposed surfaces.
• Illustrative Examples:
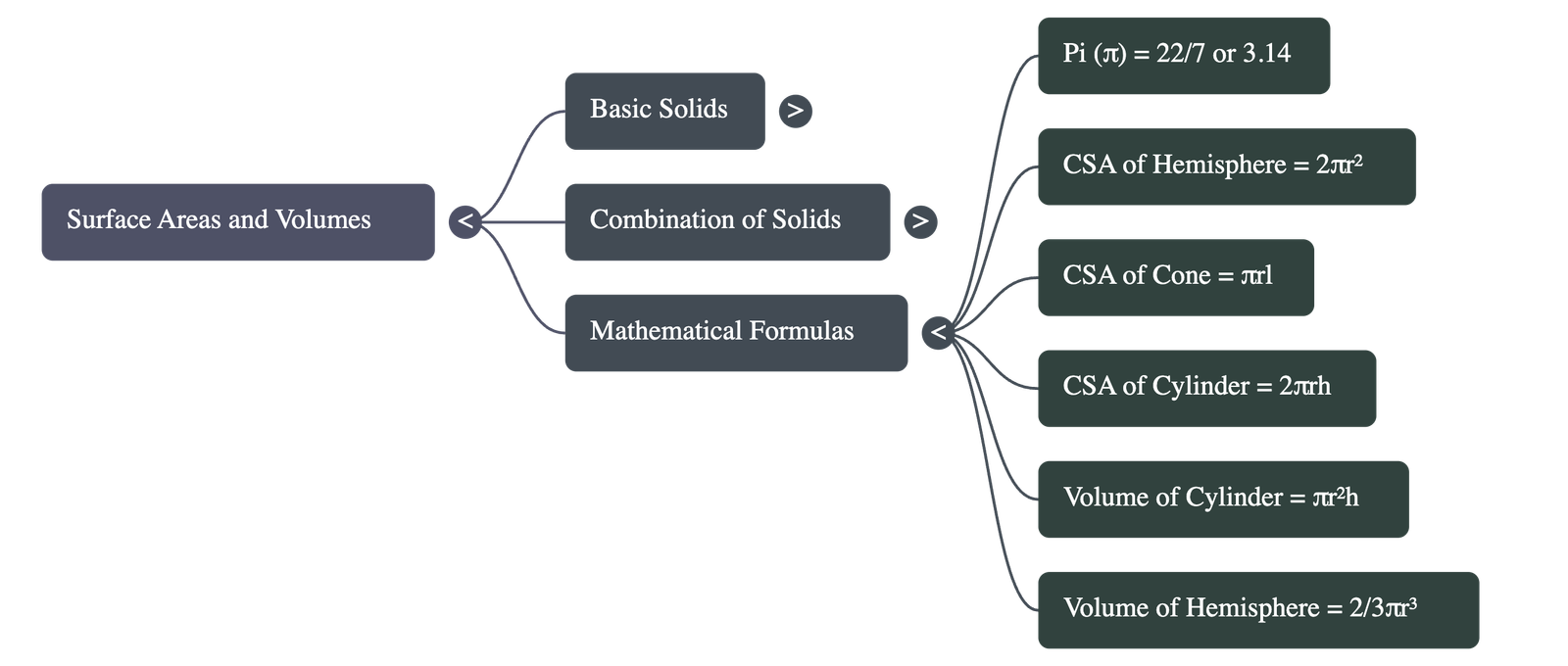
  • Toy Top (Lattu): Shaped like a cone surmounted by a hemisphere. The total surface area is the CSA of the hemisphere plus the CSA of the cone. The circular bases where they join are not calculated because they are internal.
  • Decorative Block: A cube with a hemisphere fixed on top. The surface area is the Total Surface Area (TSA) of the cube, minus the base area of the hemisphere (which covers part of the cube), plus the CSA of the hemisphere.
  • Bird-Bath: A cylinder with a hemispherical depression hollowed out. The total surface area is the CSA of the cylinder plus the CSA of the hemisphere.

3. Volume of a Combination of Solids

Calculating volume differs slightly from surface area because internal boundaries do not reduce the total capacity.

• Key Concept: The volume of a solid formed by joining two basic solids is simply the sum of the volumes of the constituents.
• Illustrative Examples:
  • Industrial Shed: Shaped like a cuboid topped by a half-cylinder. The total volume is the volume of the cuboid portion plus one-half the volume of the cylinder.
  • Solid Toy: A cone standing on a hemisphere. The total volume is the volume of the cone plus the volume of the hemisphere.
• Calculating Capacity vs. Volume:
  • Sometimes solids have depressions that reduce capacity. For example, a glass with a raised hemispherical bottom has an "apparent capacity" (volume of the cylinder) and an "actual capacity" (volume of cylinder minus volume of the hemisphere).

4. Chapter Summary

• ✔ Surface Area: To determine the surface area of an object formed by combining basic solids (cuboid, cone, cylinder, sphere, hemisphere), identify the visible surfaces and sum their areas.
• ✔ Volume: To find the volume of combined objects, calculate the volume of each individual constituent solid and add them together. If a portion is hollowed out, that volume is subtracted.