Quick Navigation:
| | |
Some Applications of Trigonometry
1. Introduction: Heights and Distances
- This chapter explores the practical application of trigonometry in real-life situations.
- It builds upon the previous study of trigonometric ratios to calculate heights of objects and distances between points without needing to measure them physically.
2. Key Definitions and Concepts
-
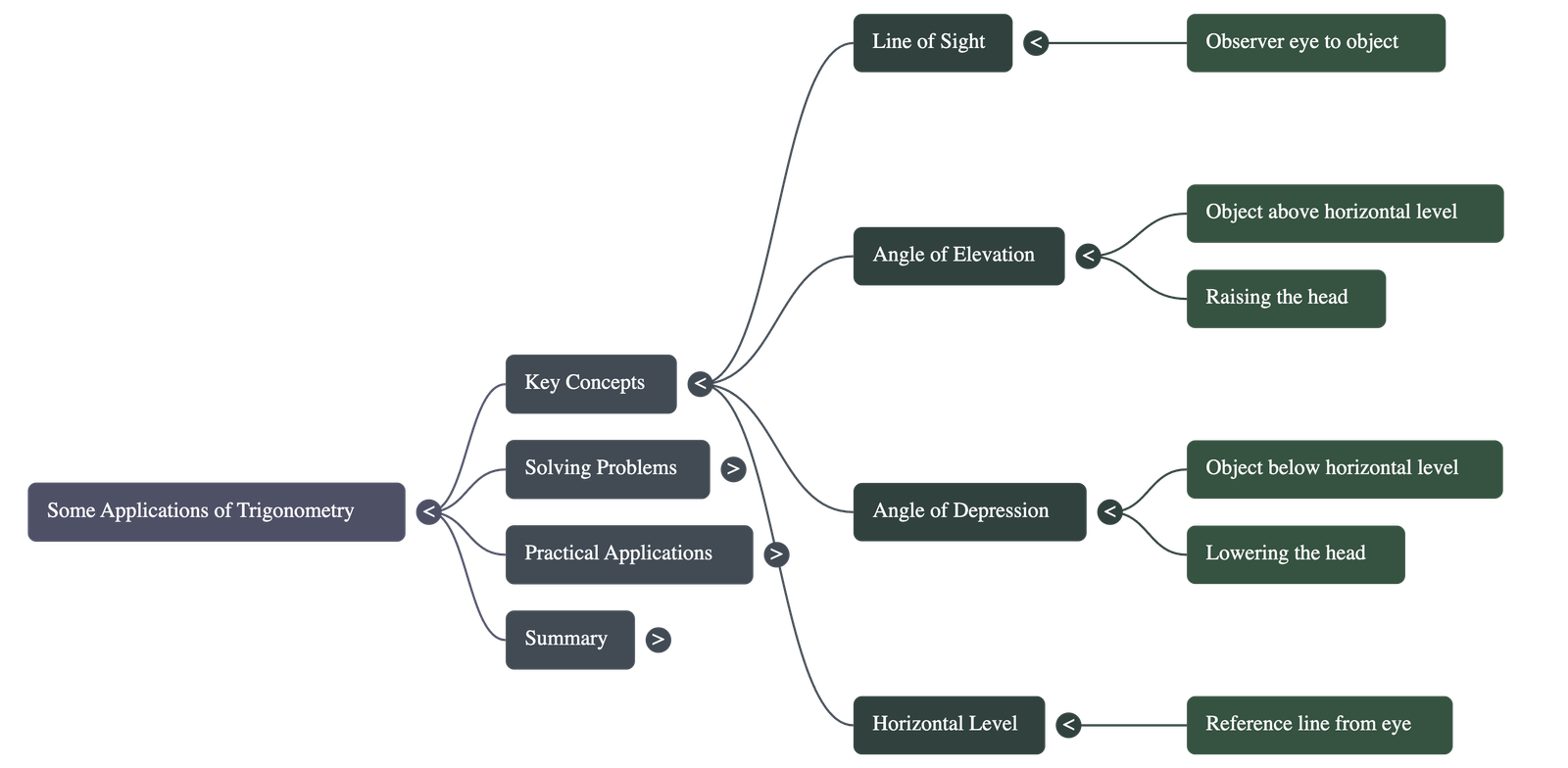
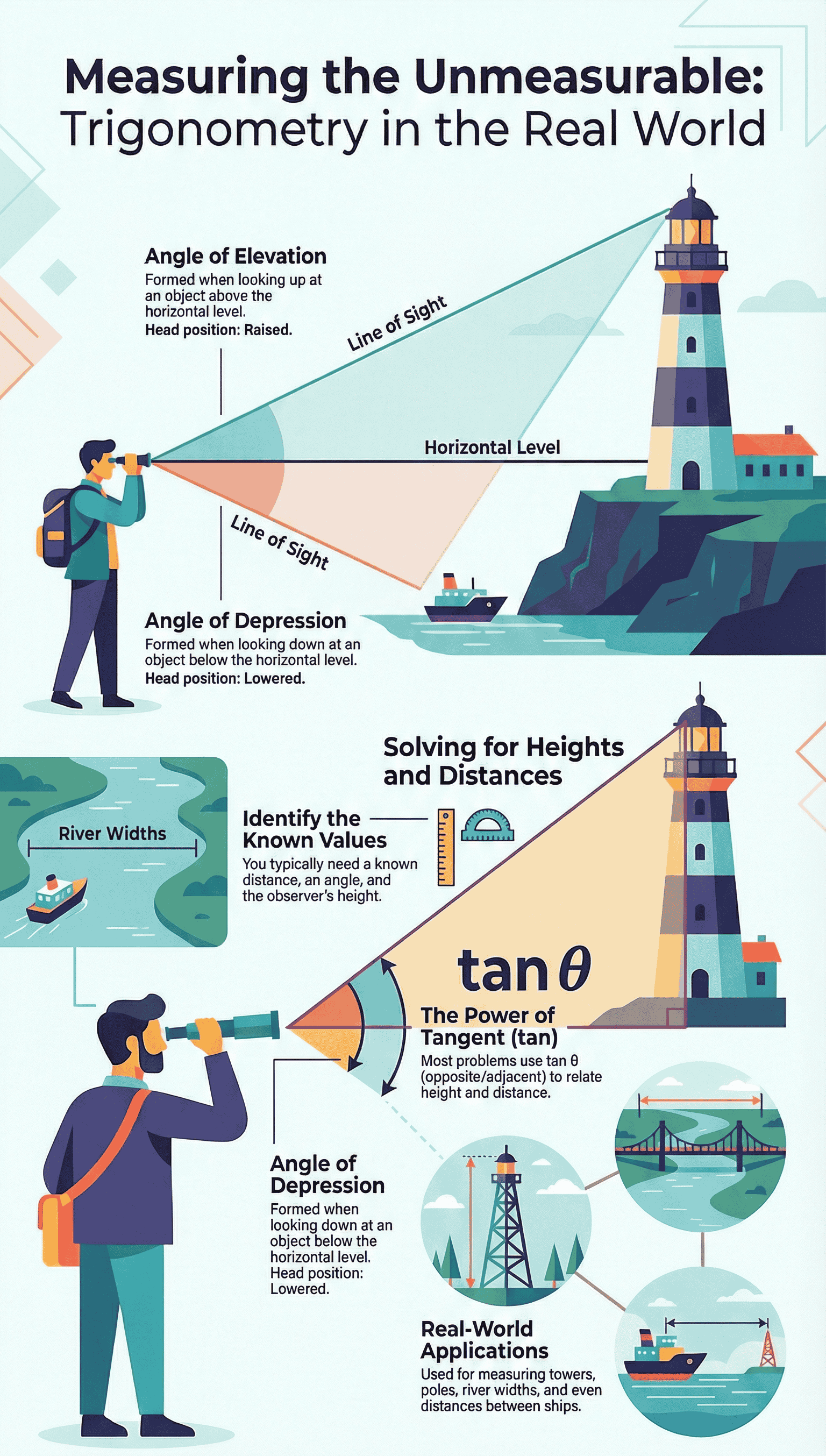
Line of Sight
The line drawn from the eye of an observer to the point in the object being viewed. -
Angle of Elevation
The angle formed by the line of sight with the horizontal line when the object being viewed is above the horizontal level. This occurs when we raise our head to look at an object. -
Angle of Depression
The angle formed by the line of sight with the horizontal line when the object being viewed is below the horizontal level. This occurs when we lower our head to look at an object.
3. Methodology for Solving Problems
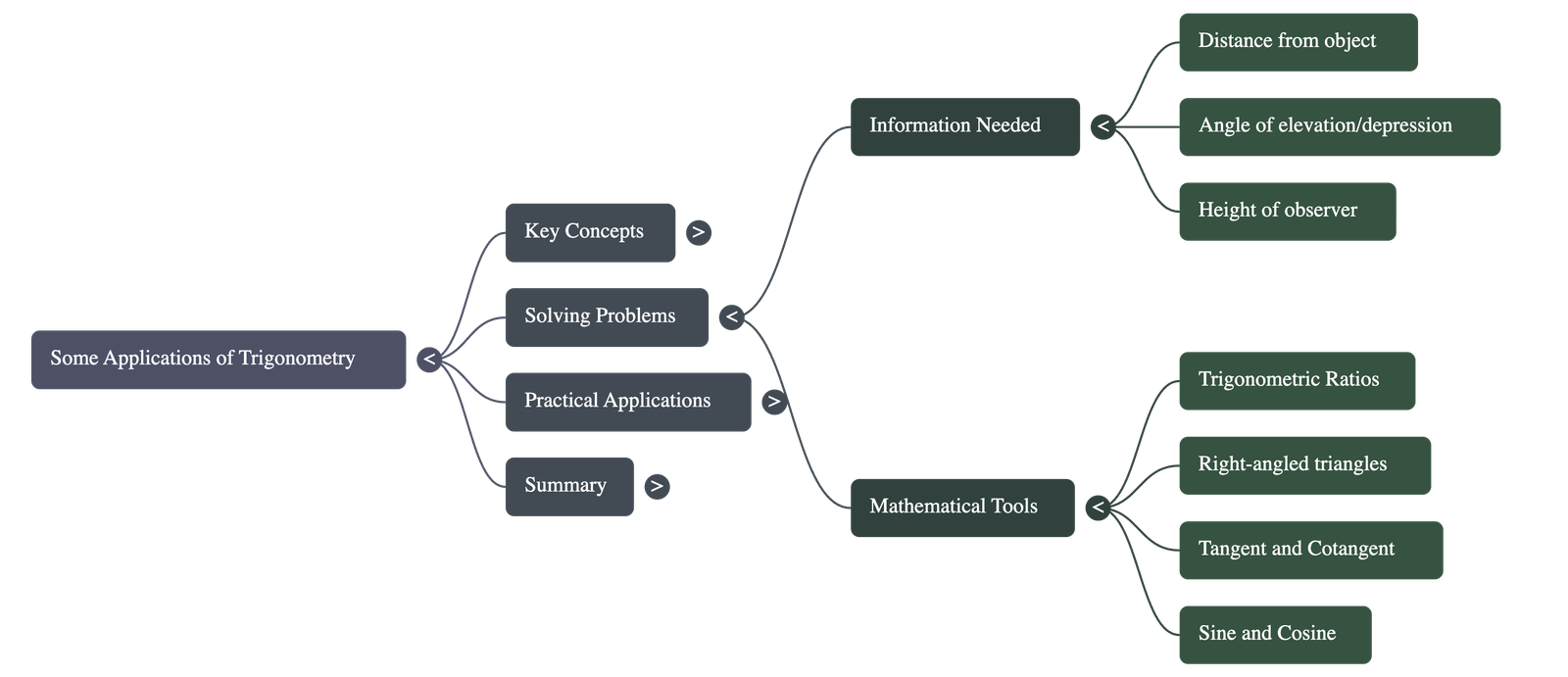
To find an unknown height or distance, the following steps are generally used:
- Draw a diagram representing the problem, identifying the observer, the object, and the horizontal level.
- Identify the formation of right-angled triangles within the figure.
- Determine the known variables (sides, angles) and the unknown variable to be found.
- Select the appropriate trigonometric ratio (sine, cosine, or tangent) that relates the known side and the unknown side with the given angle.
- Solve the equation to calculate the required height or distance.
4. Illustrative Examples Explained
A. Finding the Height of a Tower
- Given the distance from the foot of the tower and the angle of elevation of the top.
- The tangent ratio (tan) is typically used because it relates the opposite side (height) to the adjacent side (distance).
B. Complex Scenarios (Observer Height)
- If the observer has a significant height (e.g., a person 1.5m tall), the line of sight begins from their eyes, not the ground.
- The height of the observer must be added to the calculated vertical distance to find the total height of the object from the ground.
C. Two Angles of Elevation/Depression
- Flagstaff on a Building: Using two right triangles sharing a common base to find the length of a flagstaff mounted on a building.
- Shadows and Sun Altitude: Calculating the height of a tower by comparing shadow lengths at different angles of elevation of the Sun (e.g., 60° vs 30°).
- Tall vs. Short Buildings: Using angles of depression from the top of a tall building to the top and bottom of a smaller building to find heights and distances.
D. River Width from a Bridge
- Observing banks on opposite sides of a river from a point on a bridge.
- Using alternate interior angles to equate angles of depression to angles inside the triangle.
- Calculating the horizontal distance from the bridge point to each bank and summing them to find the river's width.
Chapter Summary
Trigonometry allows us to measure the unmeasurable. By understanding the relationship between the Line of Sight, the Horizontal Level, and the resulting angles (Elevation or Depression), we can utilize simple trigonometric ratios to accurately determine the heights of mountains, towers, and buildings, as well as the distances between them, using just an angle and a known length.
Quick Navigation:
| | |
1 / 1
Quick Navigation:
| | |