Pair of Linear Equations in Two Variables

1. Introduction

• Many real-life situations can be represented mathematically using linear equations.
• A general form of a linear equation in two variables is ax + by + c = 0.
• Two linear equations in the same two variables taken together form a pair of linear equations in two variables.
• Geometrically, a linear equation in two variables represents a straight line. A pair of equations represents two lines on a plane.

2. Graphical Method of Solution

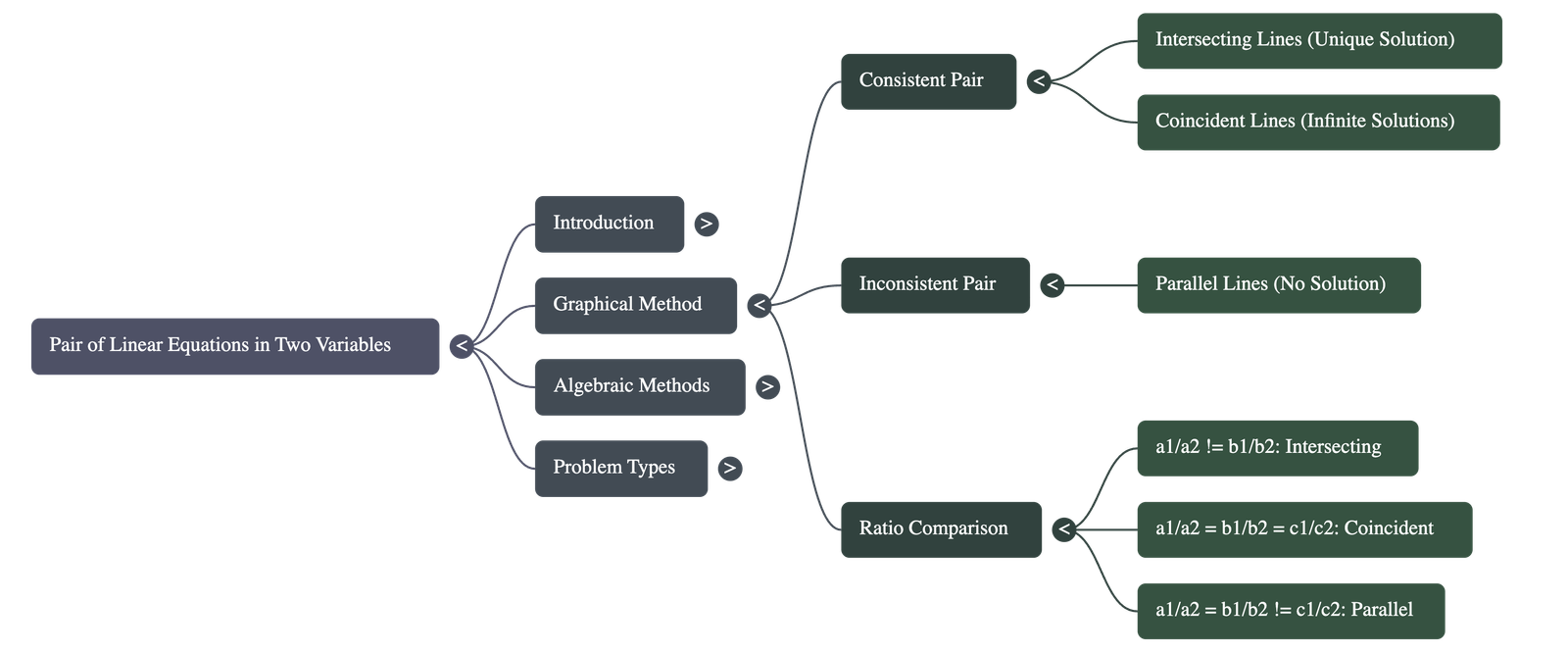
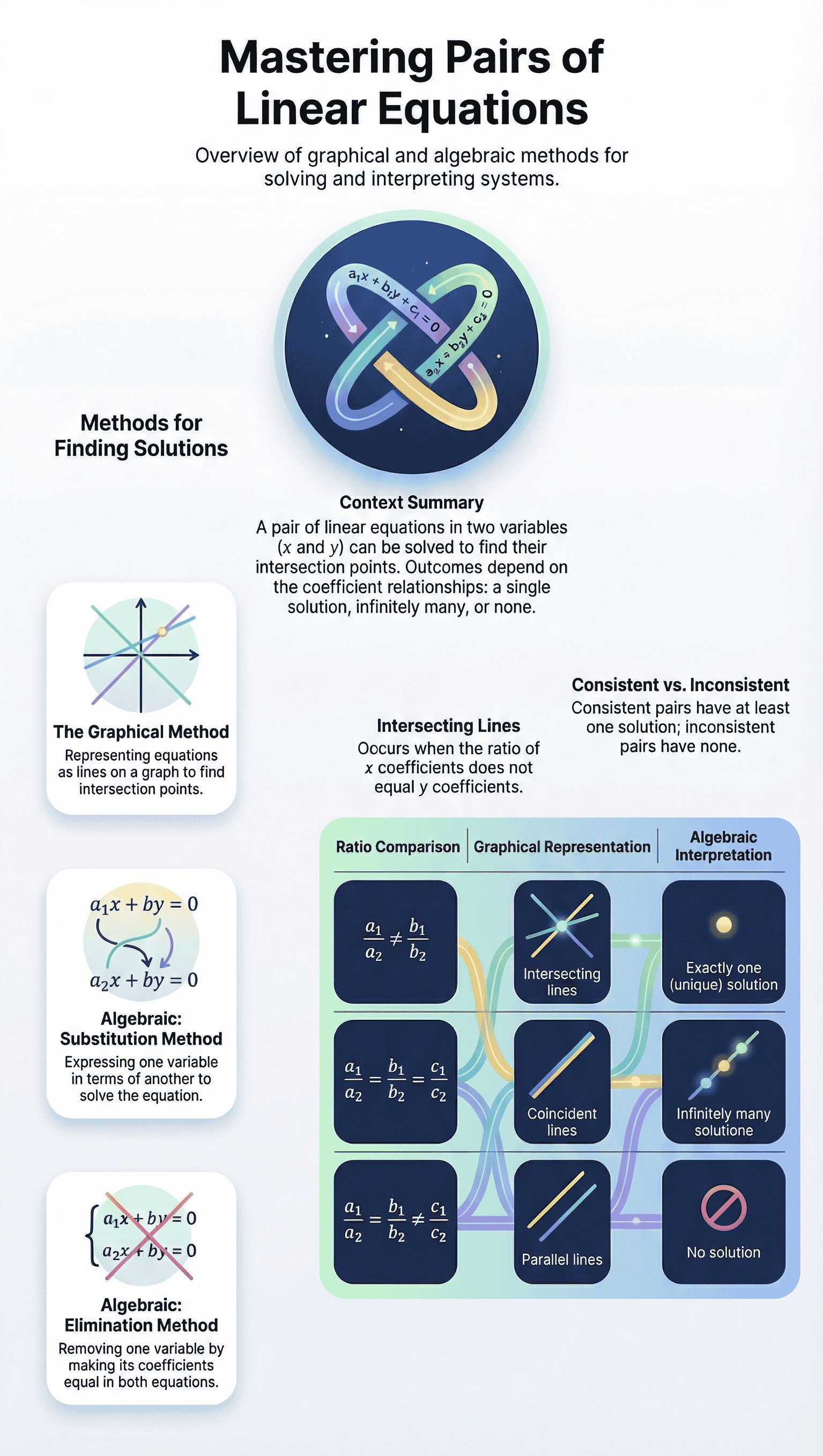
The behaviour of the two lines representing a pair of linear equations determines the nature of the solution:

• Intersecting Lines (Consistent Pair):
  If the lines intersect at a single point, the pair of equations has a unique solution.
• Coincident Lines (Dependent/Consistent Pair):
  If the lines coincide (overlap completely), the equations have infinitely many solutions because every point on the line is a solution.
• Parallel Lines (Inconsistent Pair):
  If the lines are parallel and never meet, the equations have no solution.

3. Algebraic Interpretation using Coefficients

For a pair of linear equations given by:

a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0

• Condition for Unique Solution (Intersecting Lines):
  a₁ / a₂ ≠ b₁ / b₂
• Condition for Infinitely Many Solutions (Coincident Lines):
  a₁ / a₂ = b₁ / b₂ = c₁ / c₂
• Condition for No Solution (Parallel Lines):
  a₁ / a₂ = b₁ / b₂ ≠ c₁ / c₂

4. Algebraic Methods of Solution

When graphical methods are imprecise (e.g., coordinates are non-integers), algebraic methods are used.

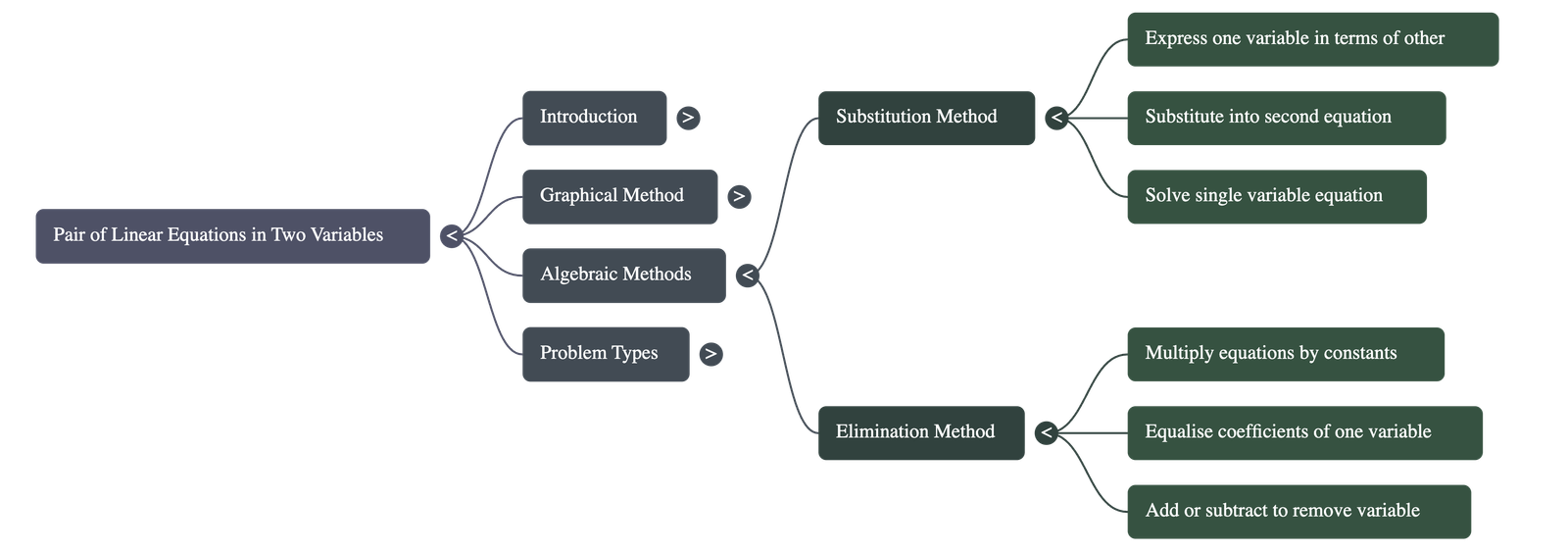
A. Substitution Method

• Step 1: Pick one equation and express one variable (say, y) in terms of the other variable (x).
• Step 2: Substitute this expression for y into the other equation. This reduces it to a linear equation in one variable.
• Step 3: Solve the resulting single-variable equation to find the value of x.
• Step 4: Substitute the value of x back into the equation from Step 1 to find the value of y.
• Note: If substitution leads to a true statement with no variables (e.g., 18=18), there are infinitely many solutions. If it leads to a false statement (e.g., 0=9), there is no solution.

B. Elimination Method

• Step 1: Multiply one or both equations by suitable constants to make the coefficients of one variable (either x or y) numerically equal.
• Step 2: Add or subtract the equations to eliminate that variable completely, resulting in an equation with a single variable.
• Step 3: Solve for the remaining variable.
• Step 4: Substitute the value found into either of the original equations to find the second variable.

5. Summary of Key Concepts

• A consistent pair of equations has at least one solution (either unique or infinite).
• An inconsistent pair of equations has no solution.
• A dependent pair of equations is always consistent and has infinitely many solutions.
• Equations that are not linear can sometimes be altered and reduced to a pair of linear equations to be solved.