Quick Navigation:
| | |
Real Numbers
1. Introduction
- This chapter continues the exploration of real numbers begun in Class IX.
- The focus lies on two important properties of positive integers:
- Euclid’s Division Algorithm: Relates to divisibility of integers. It states that any positive integer a can be divided by another positive integer b leaving a remainder r smaller than b. This is used essentially for computing the HCF (Highest Common Factor).
- The Fundamental Theorem of Arithmetic: Relates to the multiplication of positive integers. It states that every composite number can be uniquely expressed as a product of primes.
- These concepts are applied to prove the irrationality of numbers like √2, √3, and √5, and to determine the nature of decimal expansions of rational numbers.
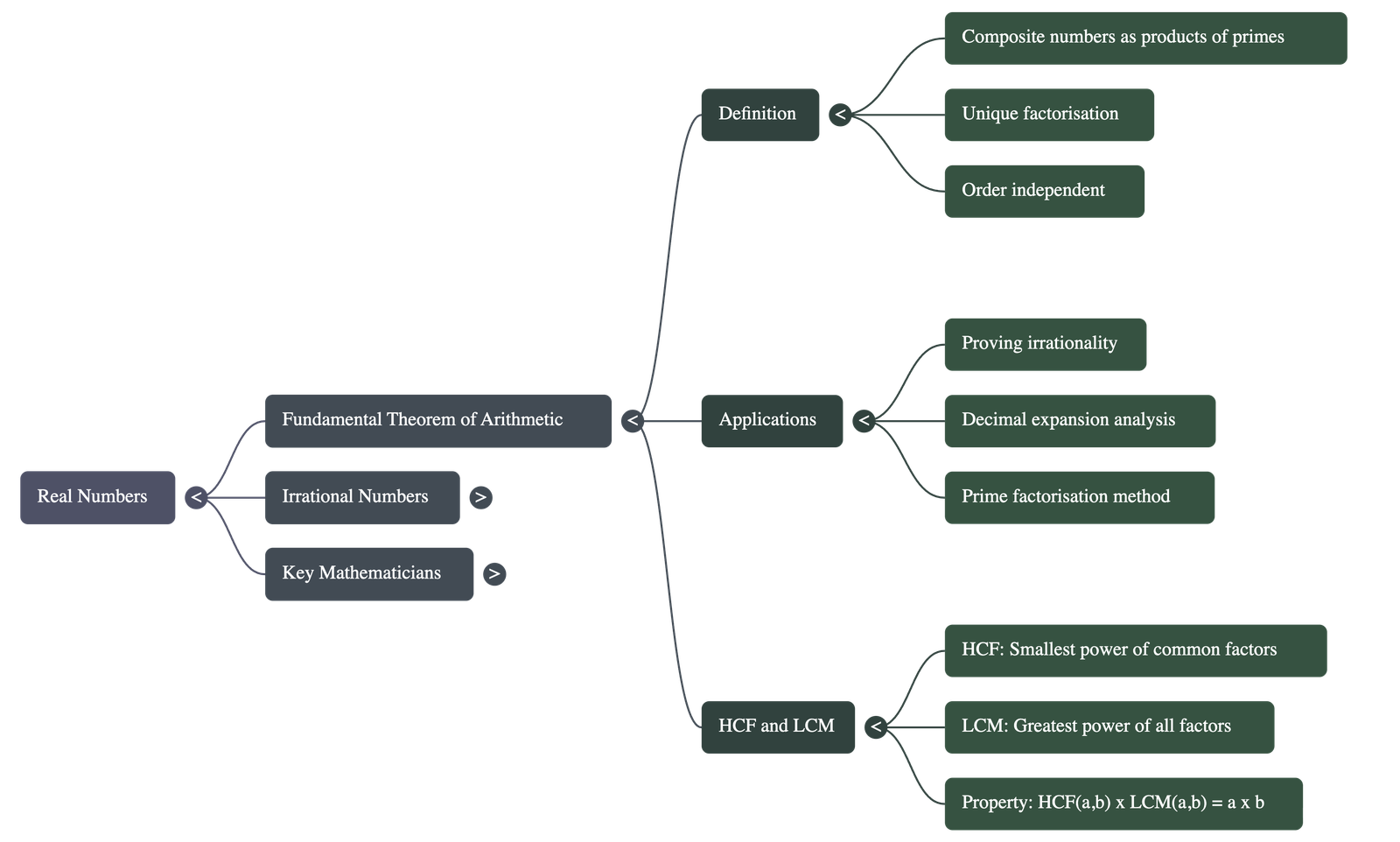
2. The Fundamental Theorem of Arithmetic
- The Theorem: Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur.
- Standard Form: Generally, primes are written in ascending order. Once the order is decided, the factorisation is unique.
- Applications:
- Divisibility Checks: The theorem can check properties of numbers, such as whether 4n can end with the digit zero. (It cannot, because the prime factorisation of 4 only contains 2, while ending in zero requires the prime factor 5).
- Finding HCF and LCM: The prime factorisation method is used to find the HCF and LCM of positive integers.
- HCF: Product of the smallest power of each common prime factor in the numbers.
- LCM: Product of the greatest power of each prime factor involved in the numbers.
- Relationship Formula: For any two positive integers a and b:
HCF(a, b) × LCM(a, b) = a × b - Important Note: The product of three numbers is not equal to the product of their HCF and LCM.
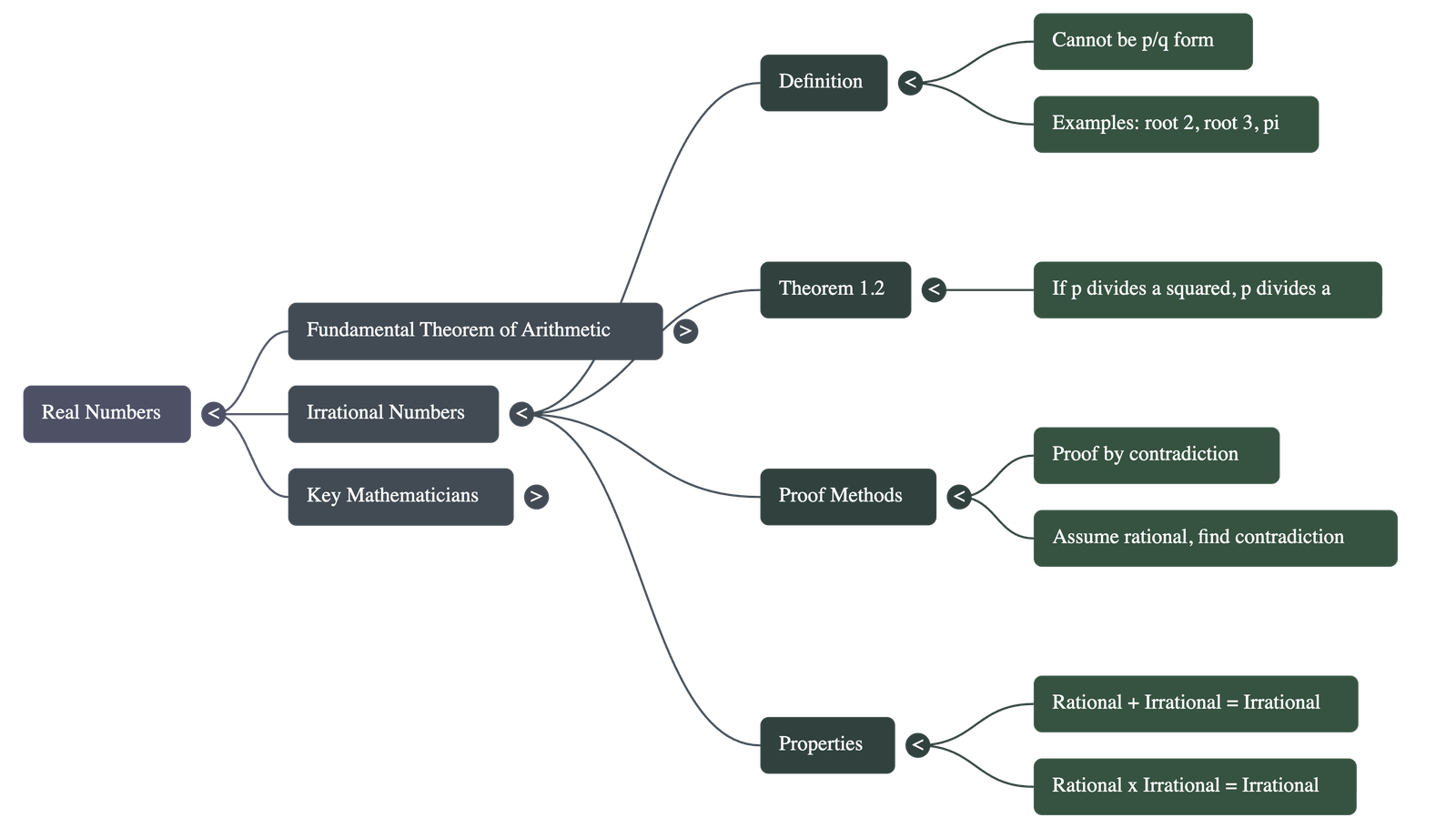
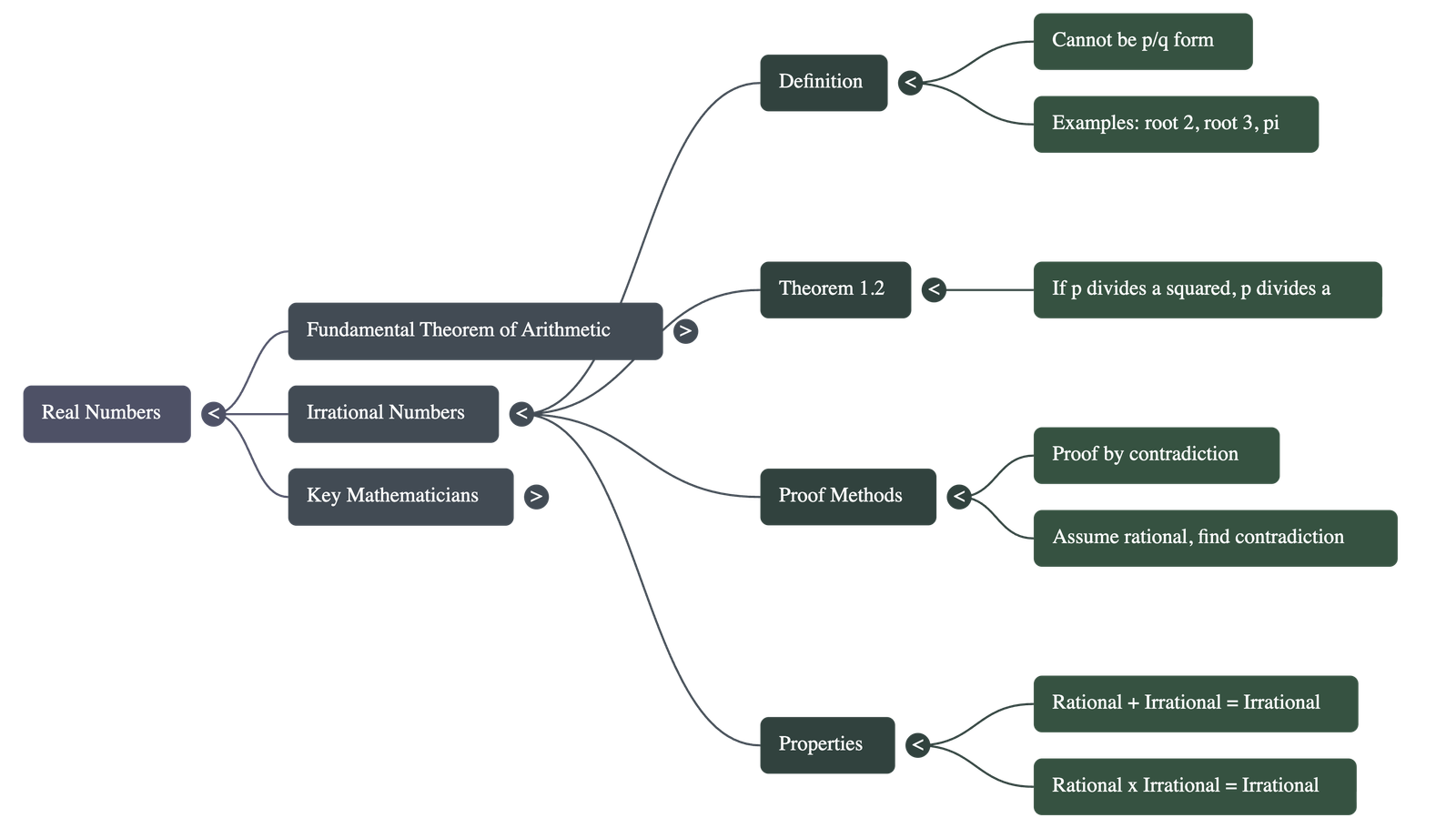
3. Revisiting Irrational Numbers
- Definition: A number s is irrational if it cannot be written in the form p/q, where p and q are integers and q ≠ 0. Examples include √2, √3, π, etc.
- Key Theorem for Proofs: Let p be a prime number. If p divides a2, then p divides a, where a is a positive integer.
- Proof by Contradiction: This technique is used to prove that numbers like √2 and √3 are irrational.
- Step 1: Assume the number is rational (i.e., can be written as a/b where a and b are coprime).
- Step 2: Square both sides and rearrange to show that a prime factor divides a.
- Step 3: Use the result to show that the same prime factor also divides b.
- Step 4: This contradicts the assumption that a and b are coprime (have no common factors). Therefore, the number is irrational.
- Properties of Irrationals:
- The sum or difference of a rational and an irrational number is irrational (e.g., 5 − √3).
- The product and quotient of a non-zero rational and an irrational number is irrational (e.g., 3√2).
Summary & Key Takeaways
- Fundamental Theorem of Arithmetic: Every composite number decomposes uniquely into prime factors.
- Prime Divisibility: If a prime p divides a2, it must divide a.
- HCF/LCM Relations:
- For two numbers: Product of numbers = HCF × LCM.
- For three numbers (p, q, r):
LCM(p, q, r) = (p × q × r × HCF(p, q, r)) / (HCF(p, q) × HCF(q, r) × HCF(p, r))
HCF(p, q, r) = (p × q × r × LCM(p, q, r)) / (LCM(p, q) × LCM(q, r) × LCM(p, r))
- Irrationality: √2, √3, and √5 are proved irrational using the Fundamental Theorem of Arithmetic and contradiction.
Quick Navigation:
| | |
1 / 1
Quick Navigation:
| | |