Chapter 10: Circles

1. Introduction to Circle Properties

• • Basic Definition: A circle is a collection of all points in a plane that are at a constant distance (radius) from a fixed point (center).
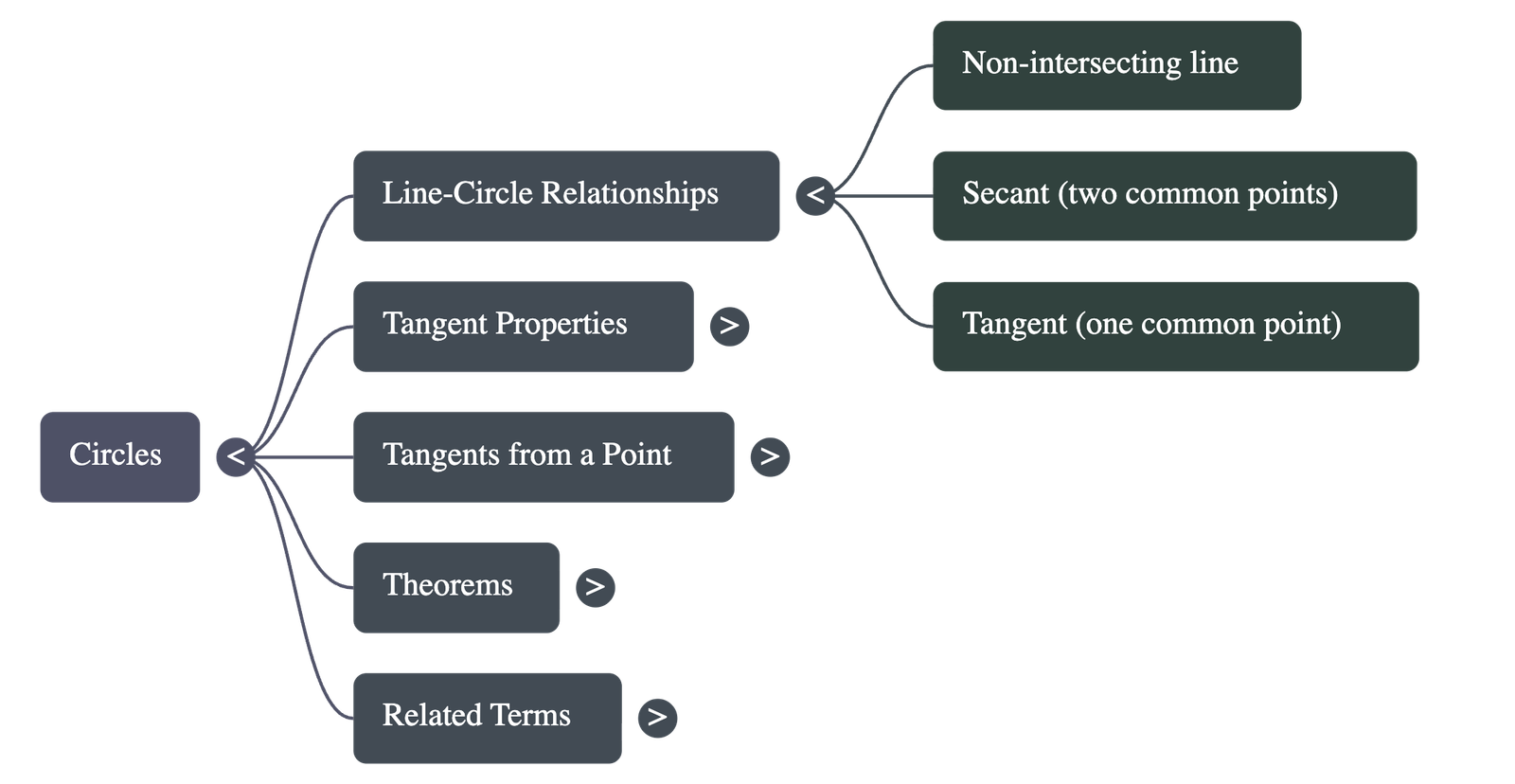
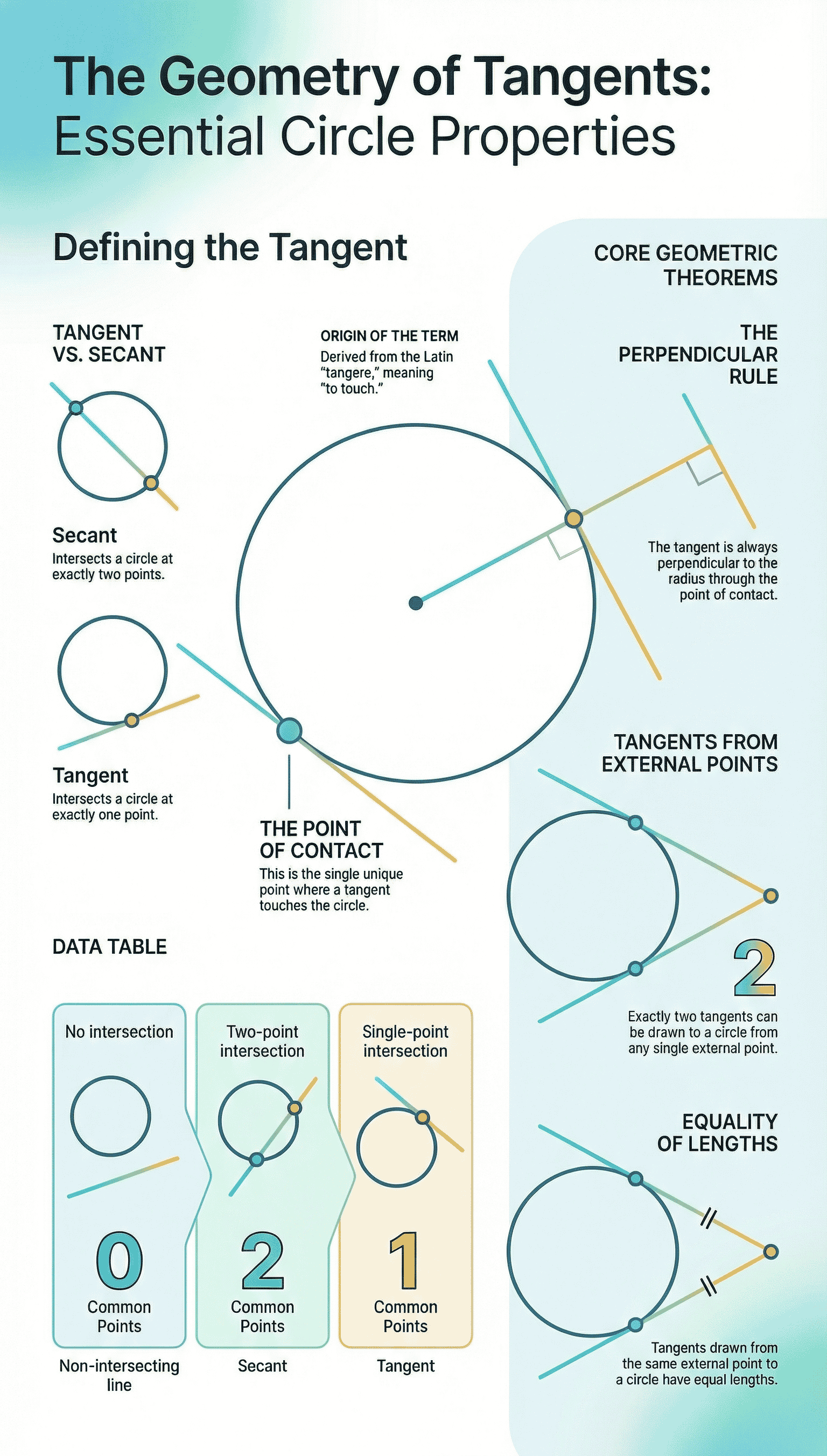
• • Positions of a Line and a Circle: When considering a circle and a line in a plane, three distinct situations exist:
  • Non-intersecting Line: The line and the circle have no common points.
  • Secant: The line intersects the circle at two distinct points.
  • Tangent: The line intersects (touches) the circle at exactly one point.

2. Tangent to a Circle

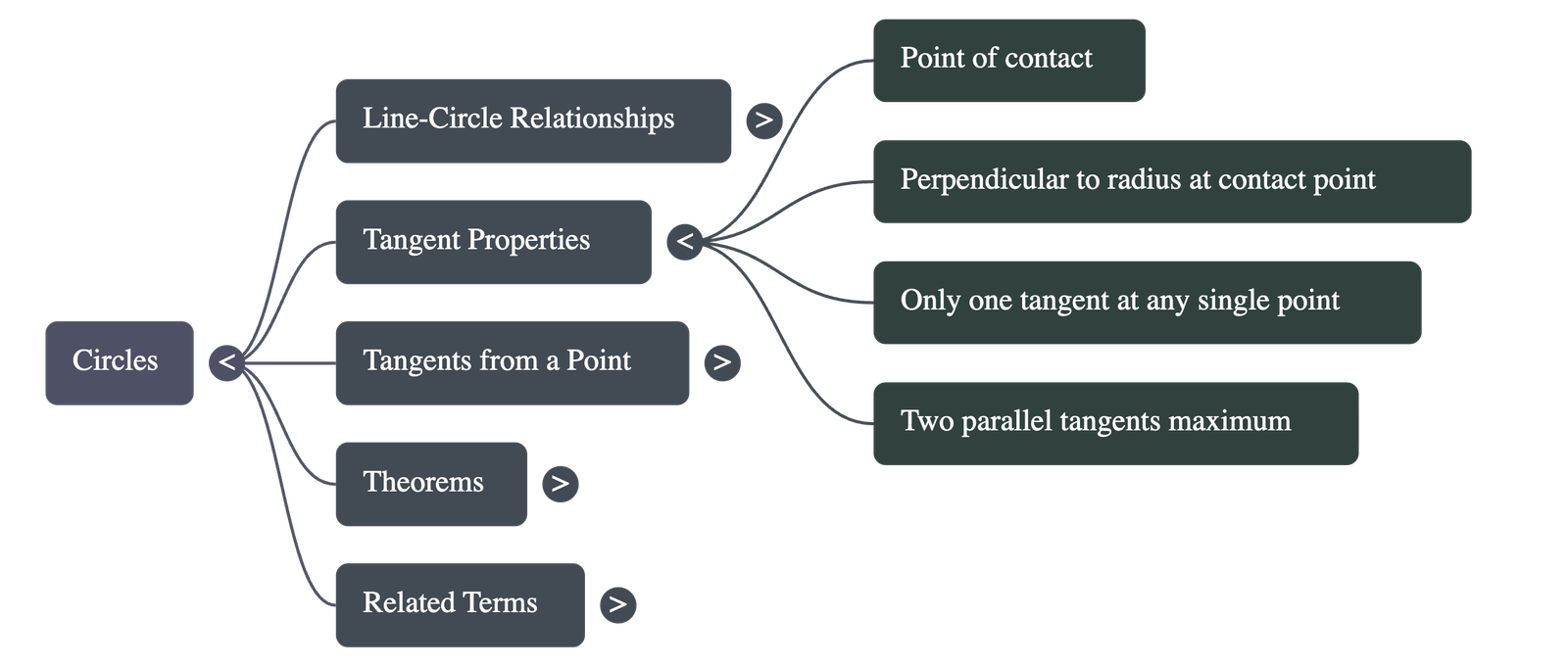
• • Definition: A tangent to a circle is a line that intersects the circle at only one point.
• • Uniqueness: There is one and only one tangent at any specific point on the circle.
• • Relation to Secant: The tangent is a special case of a secant where the two endpoints of the corresponding chord coincide.
• • Point of Contact: The common point shared by the tangent and the circle is called the point of contact. The tangent is said to "touch" the circle at this point.

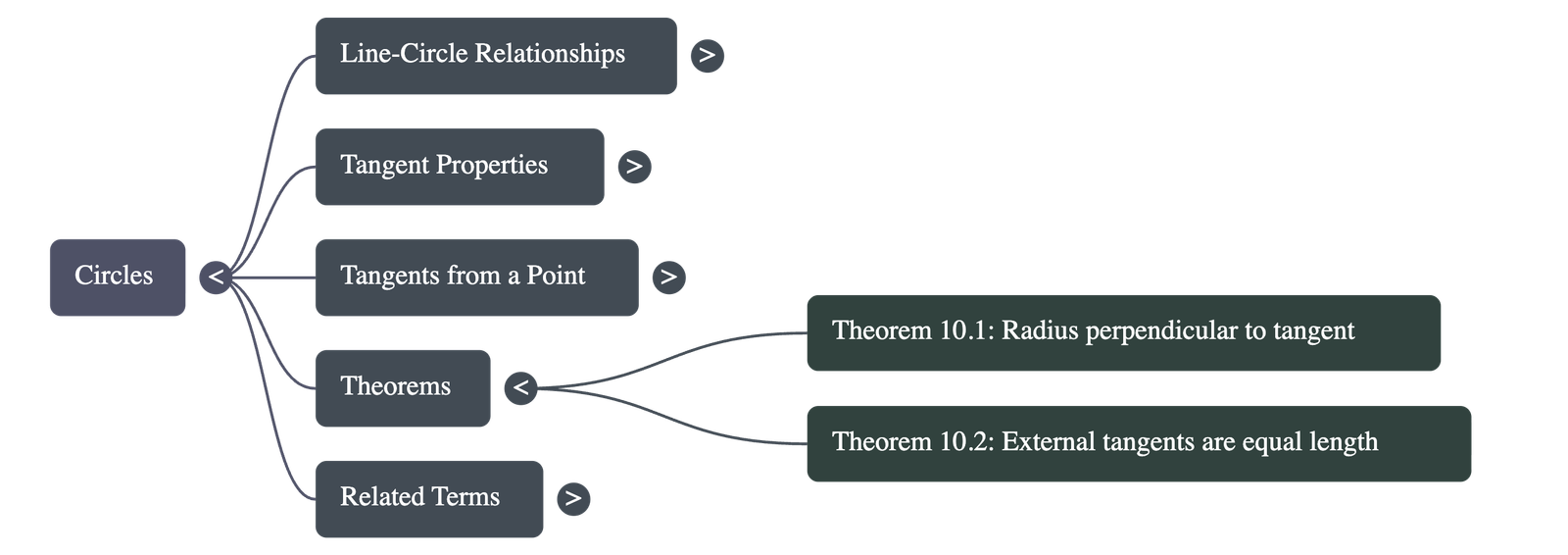
3. Theorem 10.1: Tangent-Radius Property

"The tangent at any point of a circle is perpendicular to the radius through the point of contact."

• • Proof Logic: Any point on the tangent line other than the point of contact lies outside the circle. Therefore, the distance from the center to any other point on the tangent is greater than the radius.
• • Shortest Distance: The radius is the shortest distance from the center to the tangent line, which implies perpendicularity.
• • Normal: The line containing the radius through the point of contact is sometimes called the "normal" to the circle at that point.

4. Number of Tangents from a Point

• • Point Inside the Circle: No tangent can be drawn to a circle from a point lying inside it. All lines passing through such a point are secants.
• • Point On the Circle: Exactly one tangent can be drawn to a circle at a point lying on the circle.
• • Point Outside the Circle: Exactly two tangents can be drawn to a circle from a point lying outside it.

5. Theorem 10.2: Lengths of Tangents

"The lengths of tangents drawn from an external point to a circle are equal."

• • Length Definition: The length of a tangent is the segment connecting the external point to the point of contact on the circle.
• • Associated Properties:
  • The center of the circle lies on the angle bisector of the angle formed between the two tangents.
  • The two tangents subtend equal angles at the center of the circle.

6. Key Applications and Examples

• • Concentric Circles: In two concentric circles (circles with the same center), the chord of the larger circle that touches the smaller circle is bisected at the point of contact.
• • Parallel Tangents: Tangents drawn at the ends of a diameter of a circle are parallel to each other.
• • Circumscribing Quadrilaterals:
  • Opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center.
  • If a parallelogram circumscribes a circle, it is a rhombus.