Chapter 14: Probability

1. Introduction to Probability

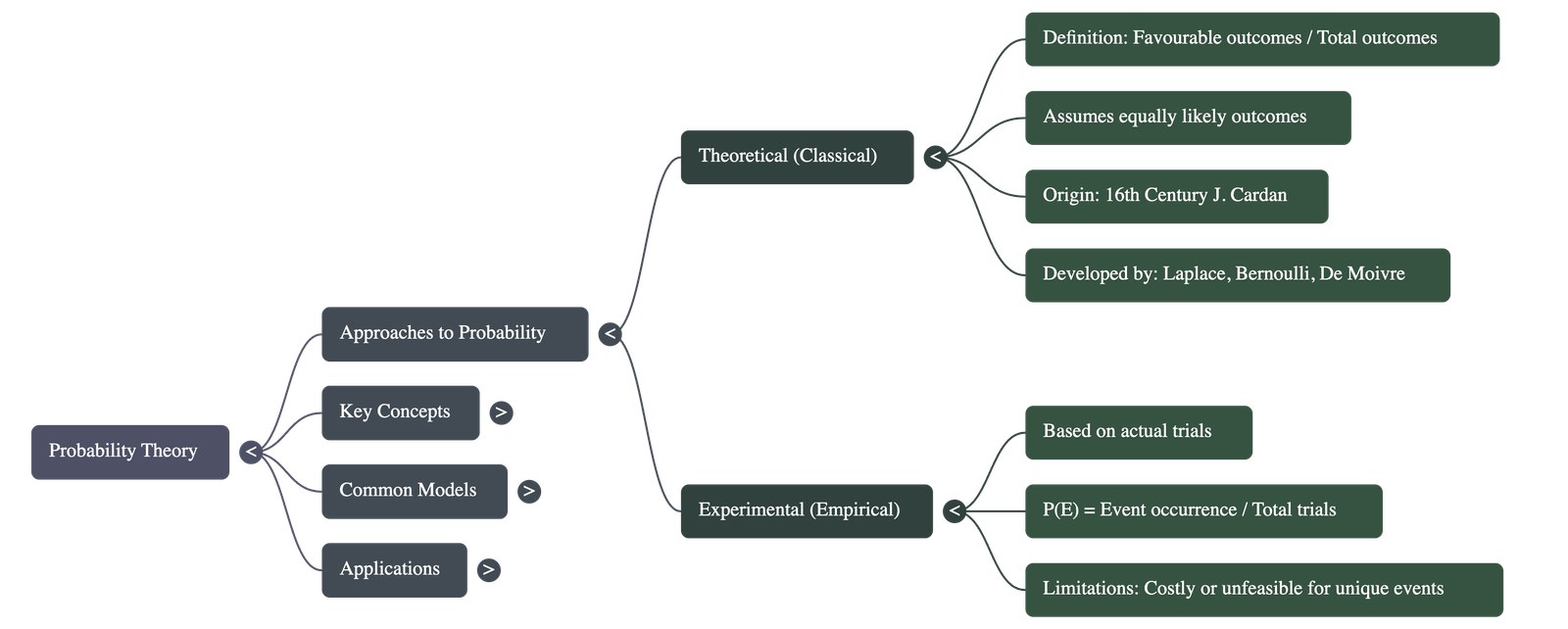
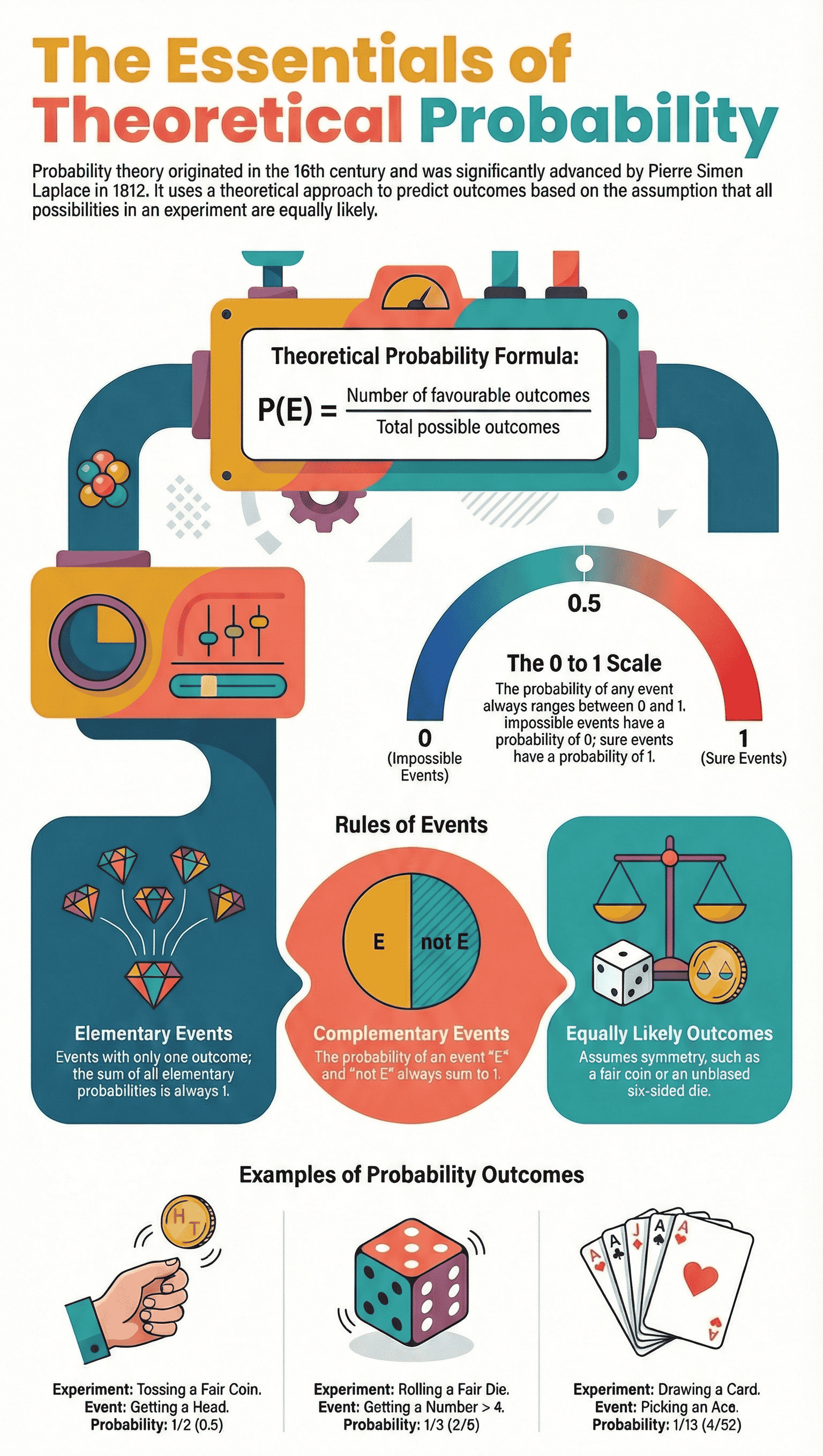
• Theoretical Approach: Unlike experimental probability, which relies on actual trials, theoretical probability predicts outcomes based on assumptions.
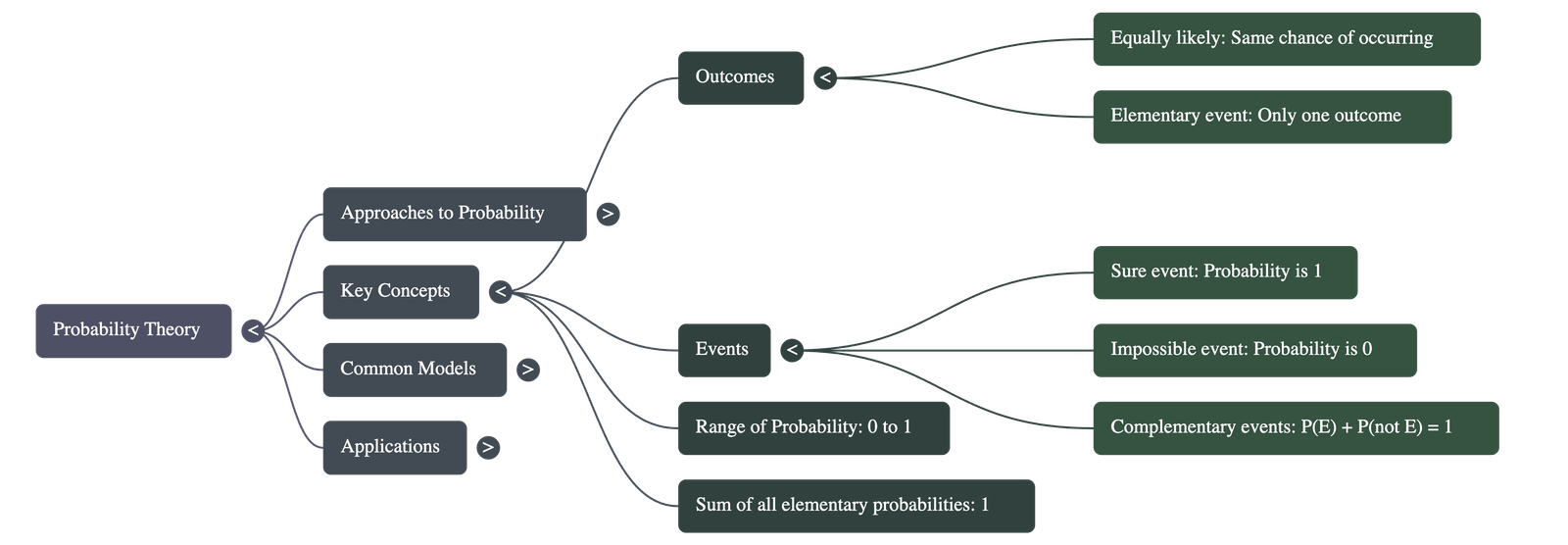
• Equally Likely Outcomes: A core assumption in this chapter is that all experiments have "equally likely outcomes," meaning no specific result is favored over another (e.g., a fair coin or a balanced die).
• Origins: The theory originated in the 16th century with J. Cardan’s The Book on Games of Chance and was further developed by mathematicians like Pierre Simon Laplace.

2. Theoretical Probability Definition

The theoretical (or classical) probability of an event E, written as P(E), is defined by the formula:

Note: This definition assumes equally likely outcomes.

3. Types of Events and Properties

• Elementary Event: An event having only one outcome of the experiment.
  Example: Getting a Head in a coin toss.
• Sum of Probabilities: The sum of the probabilities of all the elementary events of an experiment is always 1.
• Impossible Event: An event that is impossible to occur has a probability of 0.
  Example: Rolling an 8 on a standard six-sided die.
• Sure (Certain) Event: An event that is certain to occur has a probability of 1.
  Example: Rolling a number less than 7 on a standard die.
• Range of Probability: For any event E, the probability satisfies the inequality: 0 ≤ P(E) ≤ 1.

4. Complementary Events

• The event representing "not E" is called the complement of the event E.
• It is denoted by Ē (E-bar).
• Ideally, E and Ē are complementary events.
• Formula: P(Ē) = 1 – P(E)

5. Standard Examples Analyzed

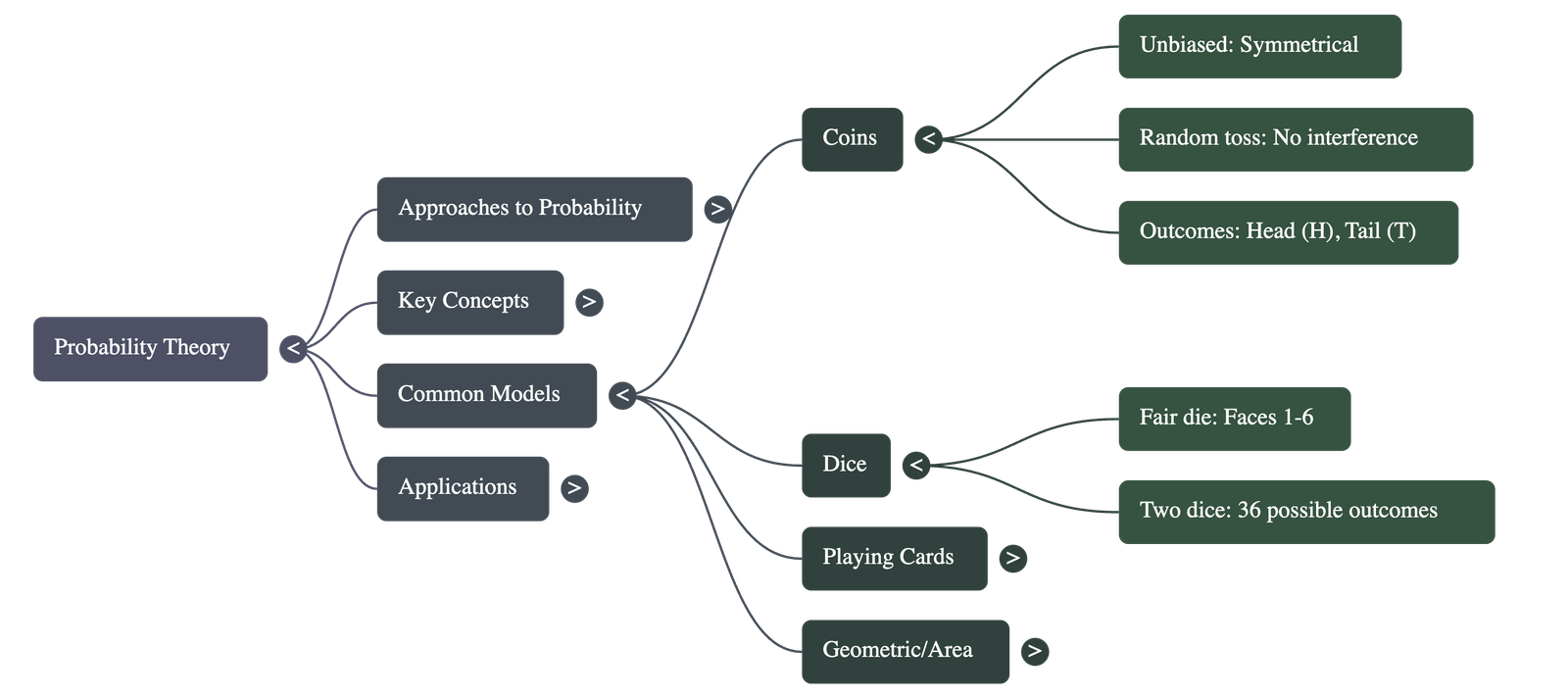
A. Coins

• One Coin: Outcomes are Head (H) and Tail (T). Total = 2.
• Two Coins: Outcomes are (H,H), (H,T), (T,H), (T,T). Total = 4.

B. Dice

• Single Die: Outcomes are 1, 2, 3, 4, 5, 6. Total = 6.
• Two Dice: Total outcomes = 6 × 6 = 36.
  Key sums and pairs are often calculated from this set (e.g., getting a doublet like (1,1), (2,2), etc.).

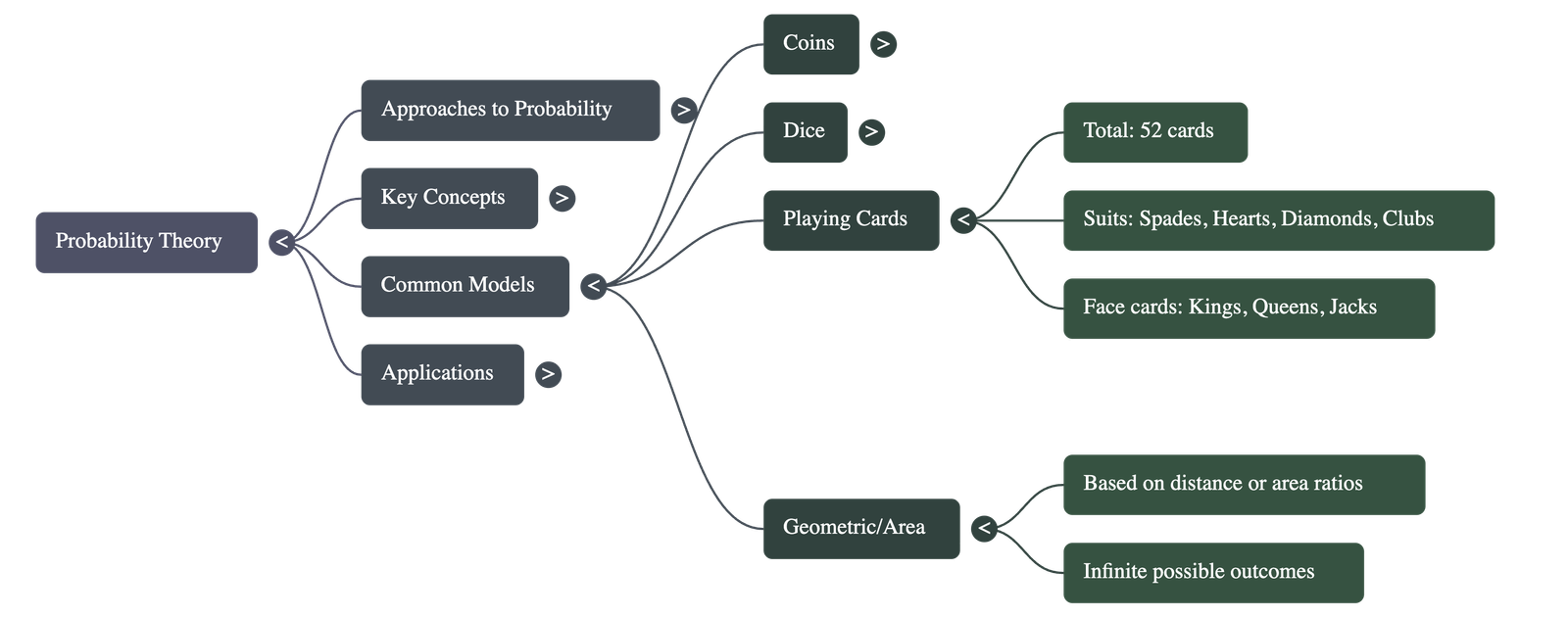
C. Playing Cards

A standard deck has 52 cards divided into:

• 4 Suits: Spades (Black), Clubs (Black), Hearts (Red), Diamonds (Red). Each suit has 13 cards.
• Face Cards: Kings, Queens, and Jacks. There are 12 face cards in total (3 per suit).
• Aces: There are 4 aces in a deck.

D. Geometric Probability

Probability can be applied to continuous areas (e.g., a helicopter crashing in a lake within a forest). The probability is calculated as the Area of the favorable region divided by the Total Area.