Quick Navigation:
| | |
INTRODUCTION TO TRIGONOMETRY
1. Introduction and Origins
- Definition: Trigonometry is the branch of mathematics dealing with the relationships between the sides and angles of a triangle.
- Etymology: The word is derived from the Greek words 'tri' (three), 'gon' (sides), and 'metron' (measure).
- Historical Context:
- Early records exist from Egypt and Babylon.
- Ancient astronomers used it to calculate distances to stars and planets.
- The concept of "sine" was first used in the work Aryabhatiyam by Aryabhata (A.D. 500). The term evolved from ardha-jya to jiva, then to the Latin sinus.
- Modern Application: It forms the basis for technologically advanced methods in Engineering and Physical Sciences.
2. Trigonometric Ratios
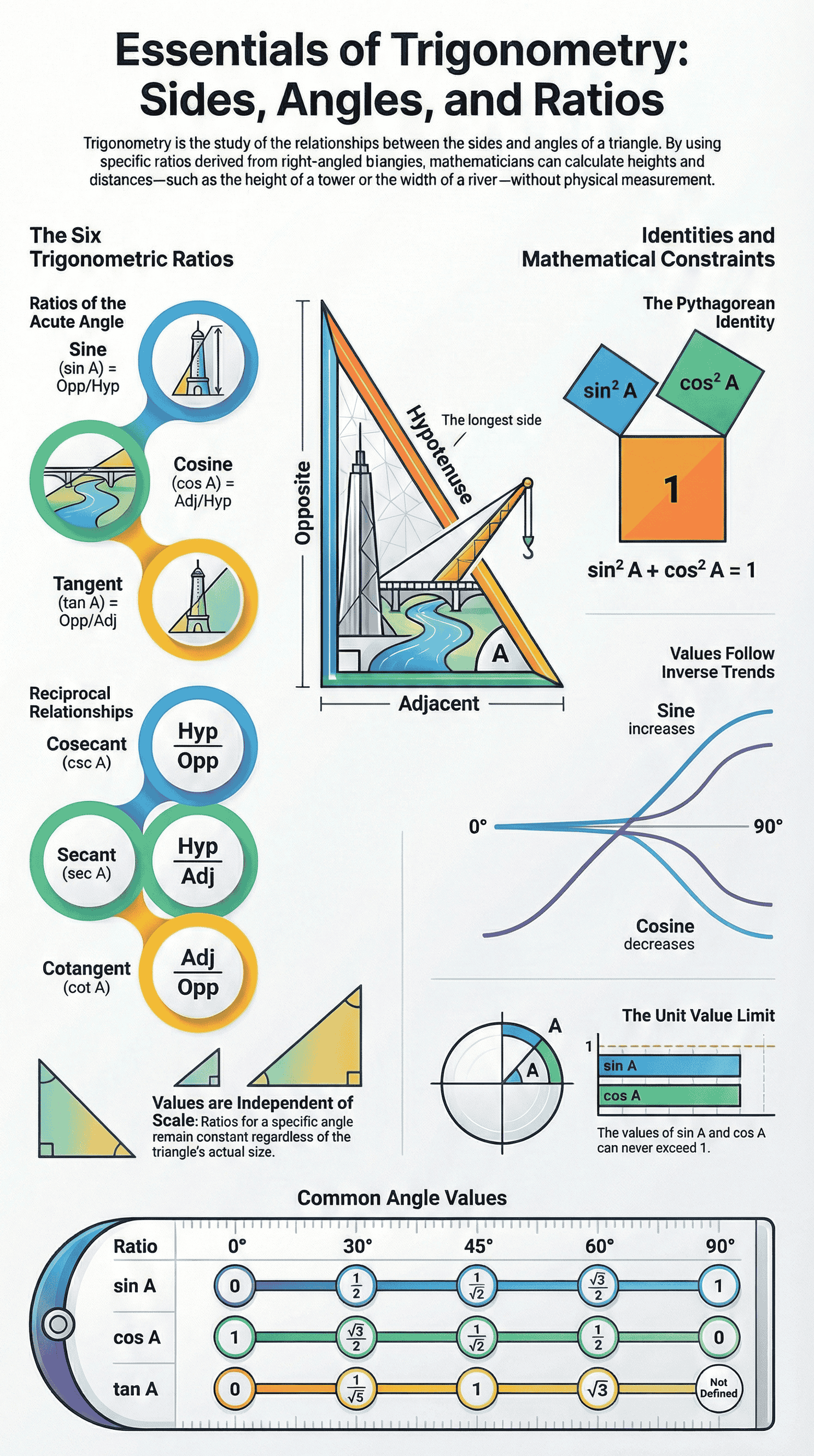
Trigonometric ratios express the relationship between an acute angle in a right triangle and the lengths of its sides.
Definitions based on a Right Triangle ABC (angle B = 90°):
For an acute angle A:
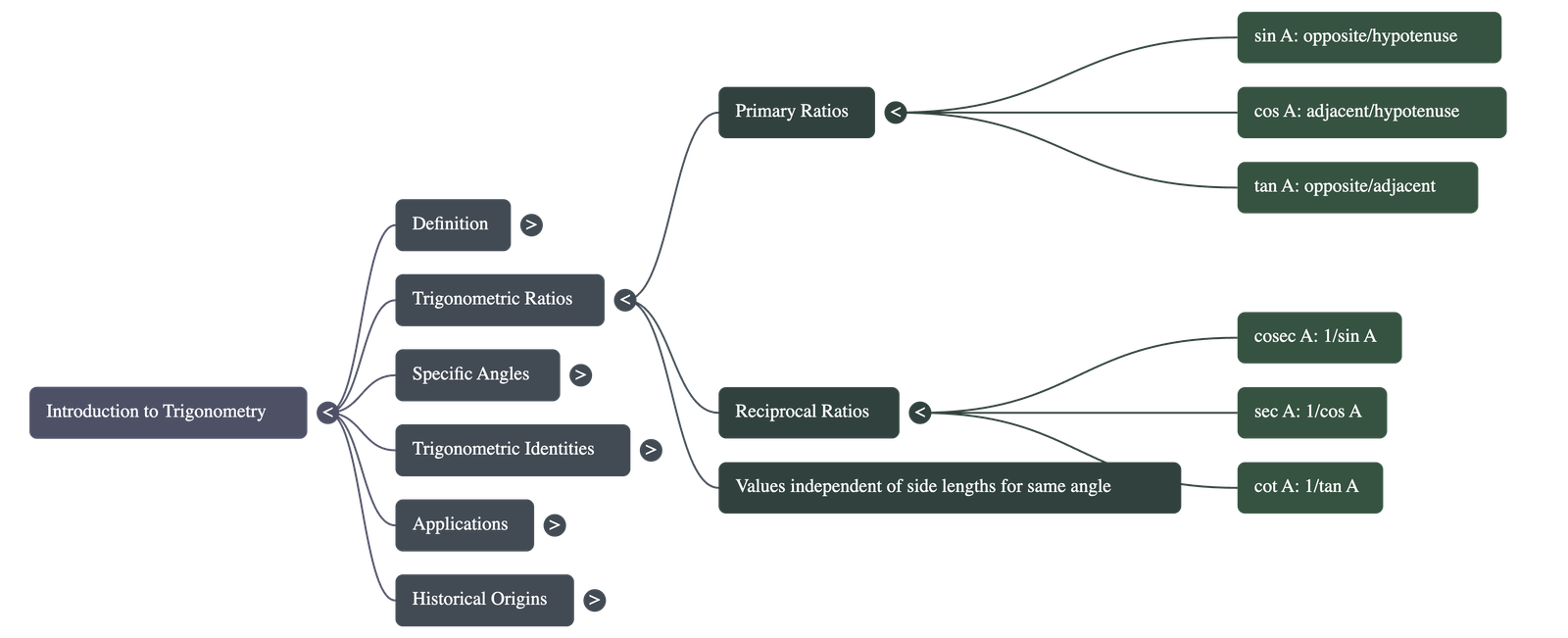
- Sine (sin A): Ratio of the side opposite to angle A to the hypotenuse.
sin A = Opposite / Hypotenuse - Cosine (cos A): Ratio of the side adjacent to angle A to the hypotenuse.
cos A = Adjacent / Hypotenuse - Tangent (tan A): Ratio of the side opposite to angle A to the side adjacent to angle A.
tan A = Opposite / Adjacent
Reciprocal Ratios:
- Cosecant (cosec A): Reciprocal of sine.
cosec A = 1 / sin A = Hypotenuse / Opposite - Secant (sec A): Reciprocal of cosine.
sec A = 1 / cos A = Hypotenuse / Adjacent - Cotangent (cot A): Reciprocal of tangent.
cot A = 1 / tan A = Adjacent / Opposite
Key Properties:
- Quotient Relations: tan A = sin A / cos A and cot A = cos A / sin A.
- Invariance: The values of trigonometric ratios depend only on the angle, not on the size of the triangle (proven via similarity of triangles).
- Range: Since the hypotenuse is the longest side, the values of sin A and cos A are always less than or equal to 1. Consequently, sec A and cosec A are always greater than or equal to 1.
- Notation: (sin A)2 is written as sin2 A. Note that sin-1 A is different from (sin A)-1.
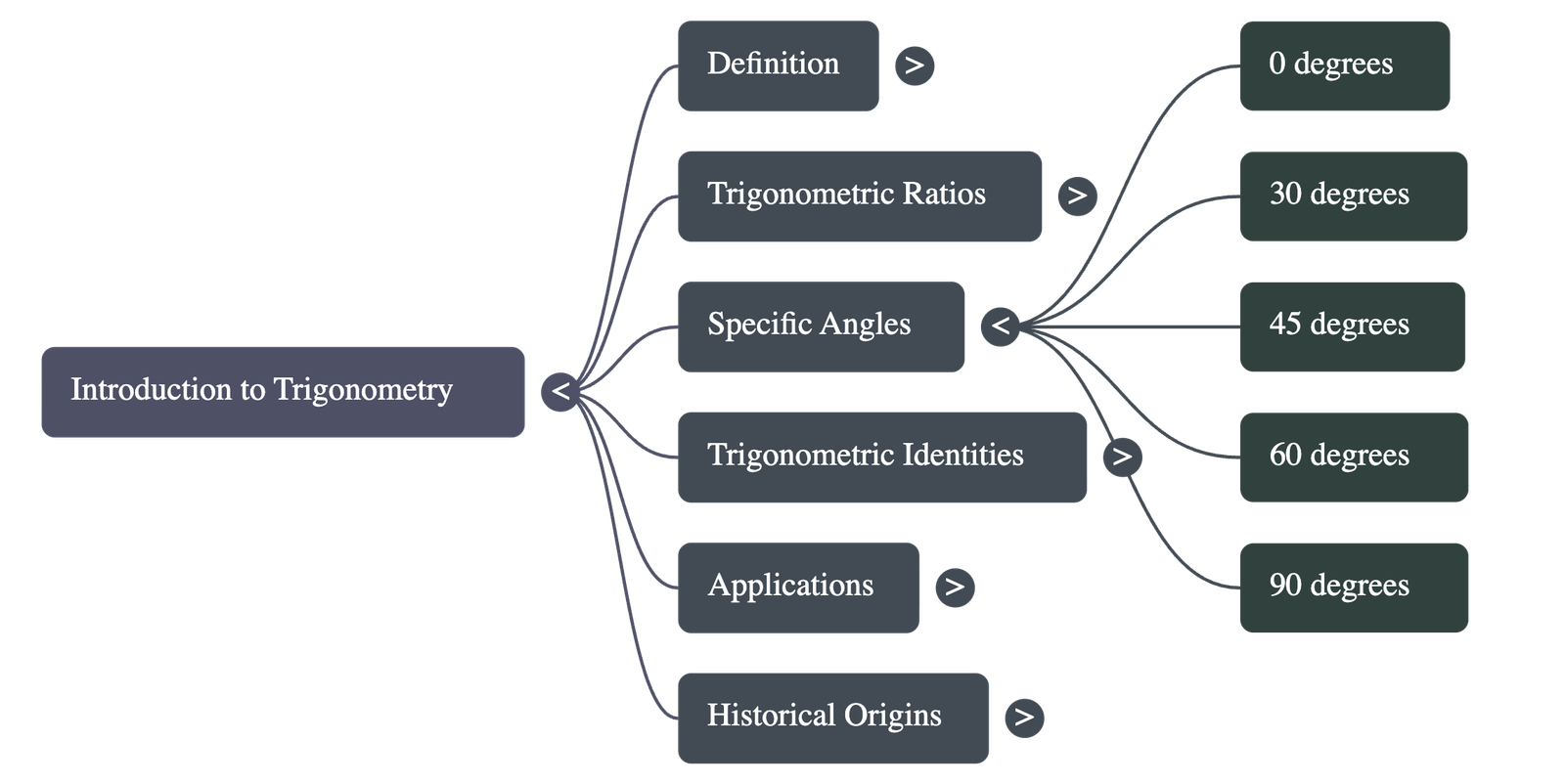
3. Trigonometric Ratios of Specific Angles
Values for specific angles (0°, 30°, 45°, 60°, 90°) are derived using geometry (equilateral and isosceles right triangles).
| Angle θ | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| tan θ | 0 | 1/√3 | 1 | √3 | Not defined |
Observations:
- As angle A increases from 0° to 90°, sin A increases from 0 to 1.
- As angle A increases from 0° to 90°, cos A decreases from 1 to 0.
- tan 90°, sec 90°, cosec 0°, and cot 0° are not defined.
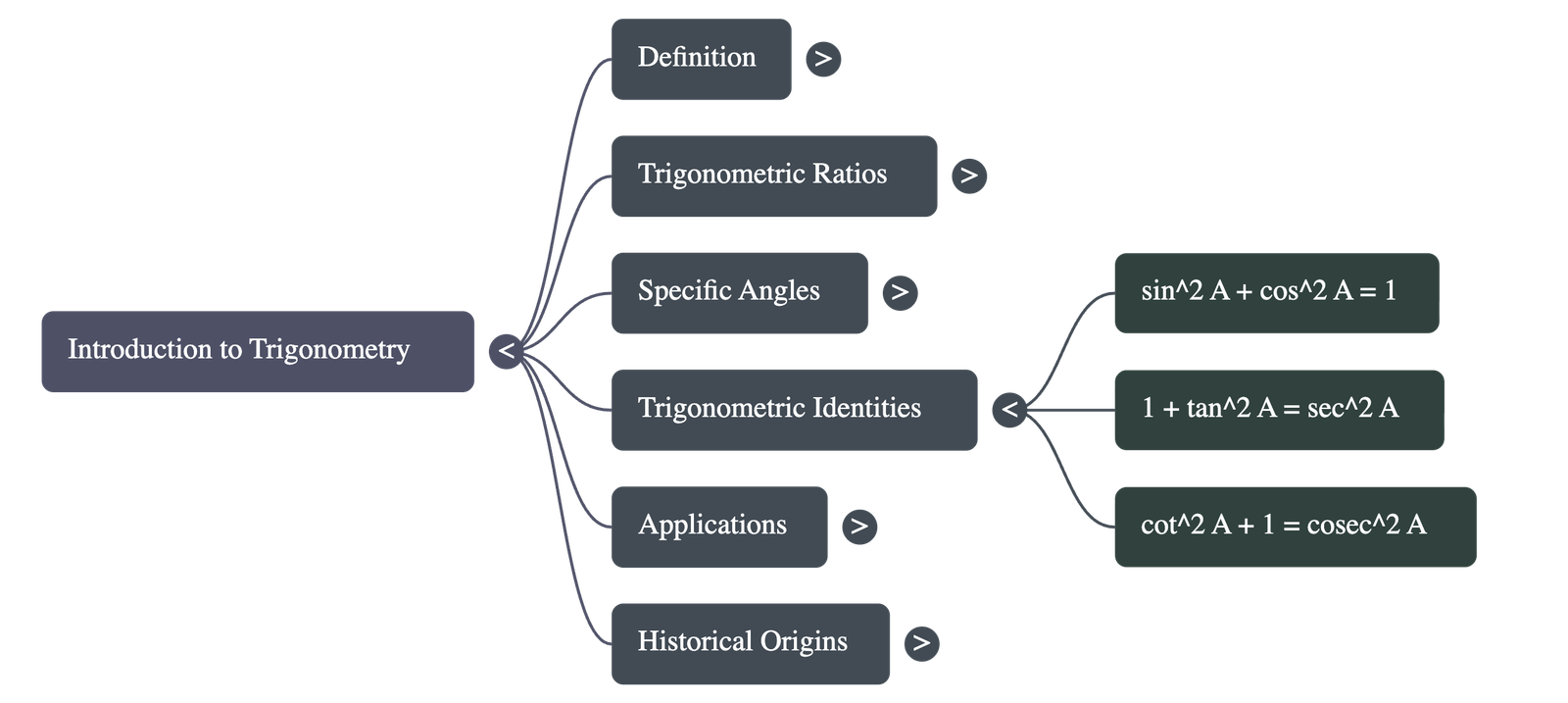
4. Trigonometric Identities
A trigonometric identity is an equation involving trigonometric ratios of an angle that is true for all values of the angle.
Fundamental Identities:
- cos2 A + sin2 A = 1
(True for 0° ≤ A ≤ 90°) - 1 + tan2 A = sec2 A
(True for 0° ≤ A < 90°) - cot2 A + 1 = cosec2 A
(True for 0° < A ≤ 90°)
Utility of Identities:
- These identities allow the expression of any trigonometric ratio in terms of another.
- Example: If sin A is known, cos A can be found using √(1 - sin2 A).
- They are used to simplify trigonometric expressions and prove other equations.
Summary derived from Chapter 8 "Introduction to Trigonometry".
Quick Navigation:
| | |
1 / 1
Quick Navigation:
| | |