Arithmetic Progressions

1. Introduction to Patterns

• Many occurrences in nature follow certain patterns, such as the petals of a sunflower, holes of a honeycomb, or spirals on a pine cone.
• Patterns also exist in daily life, such as fixed annual salary increments or the decreasing lengths of rungs on a ladder.
• In mathematics, we study specific patterns where succeeding terms are obtained by adding a fixed number to preceding terms.

2. Arithmetic Progressions (AP)

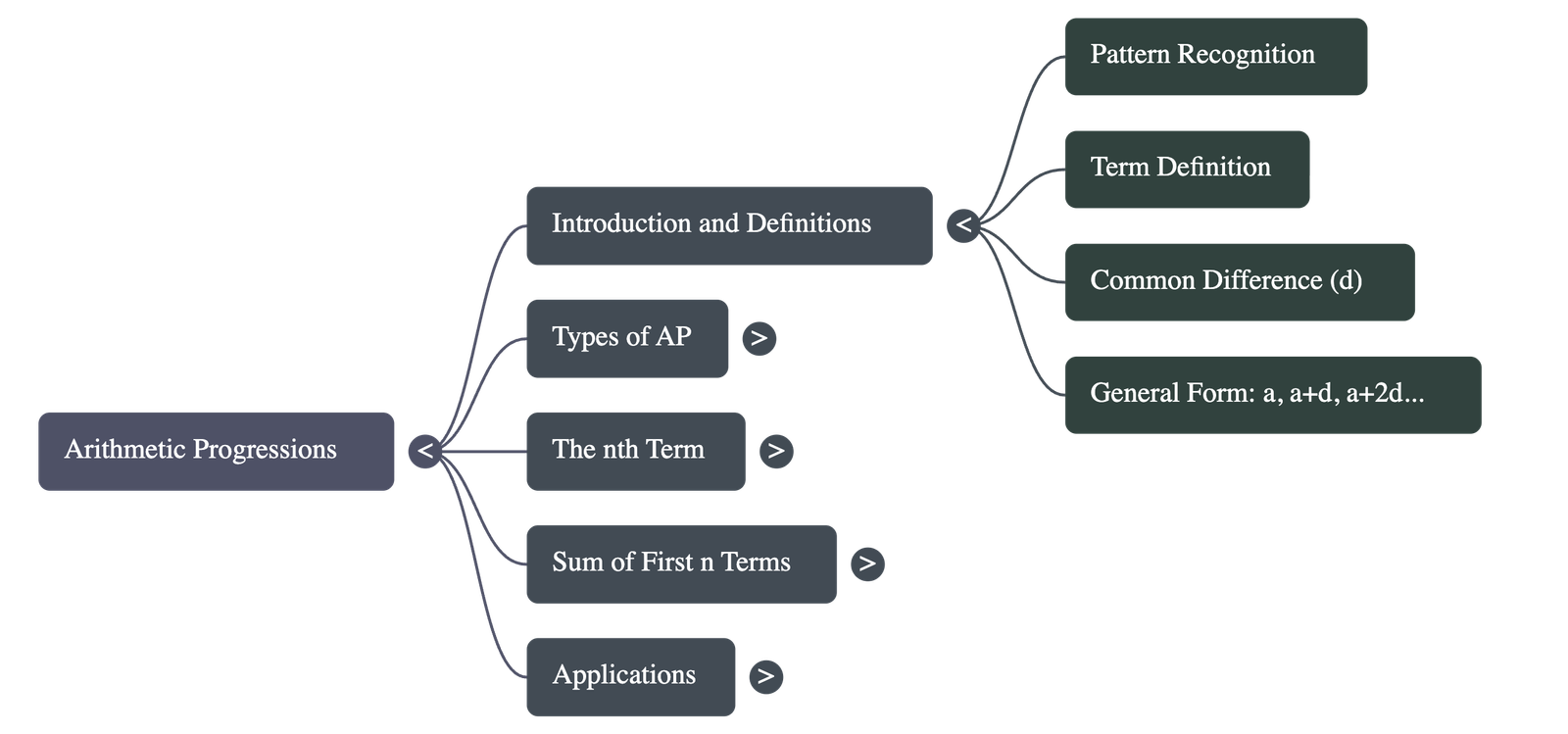
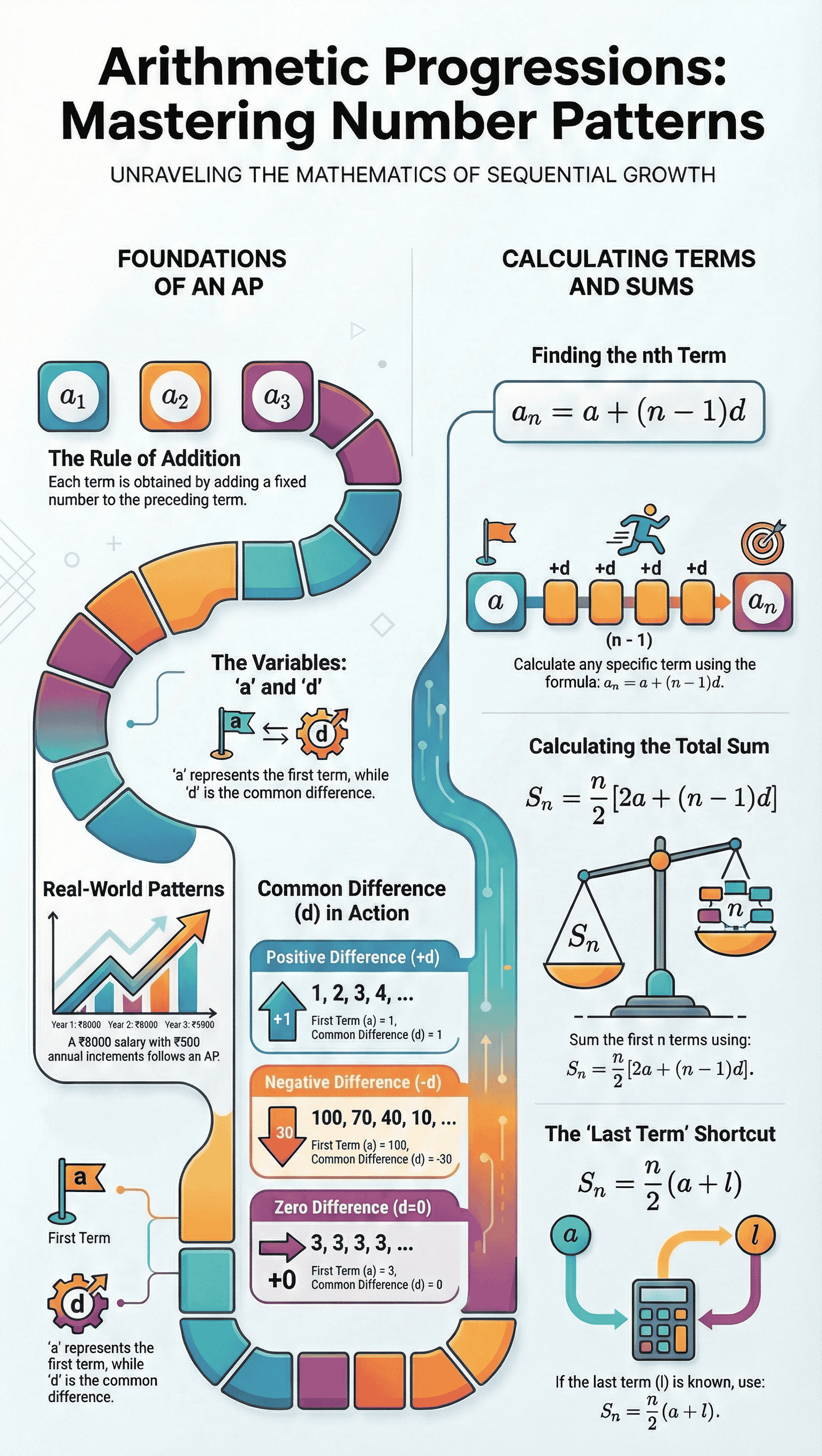
An Arithmetic Progression is a list of numbers in which each term is obtained by adding a fixed number to the preceding term, except for the first term.

Key Components:

• Terms: Each number in the list is called a term.
• Common Difference (d): The fixed number added to get the next term. It can be positive, negative, or zero.
• First Term (a): The starting number of the progression.
• General Form: An AP can be represented as:
  
  a, a + d, a + 2d, a + 3d, ...

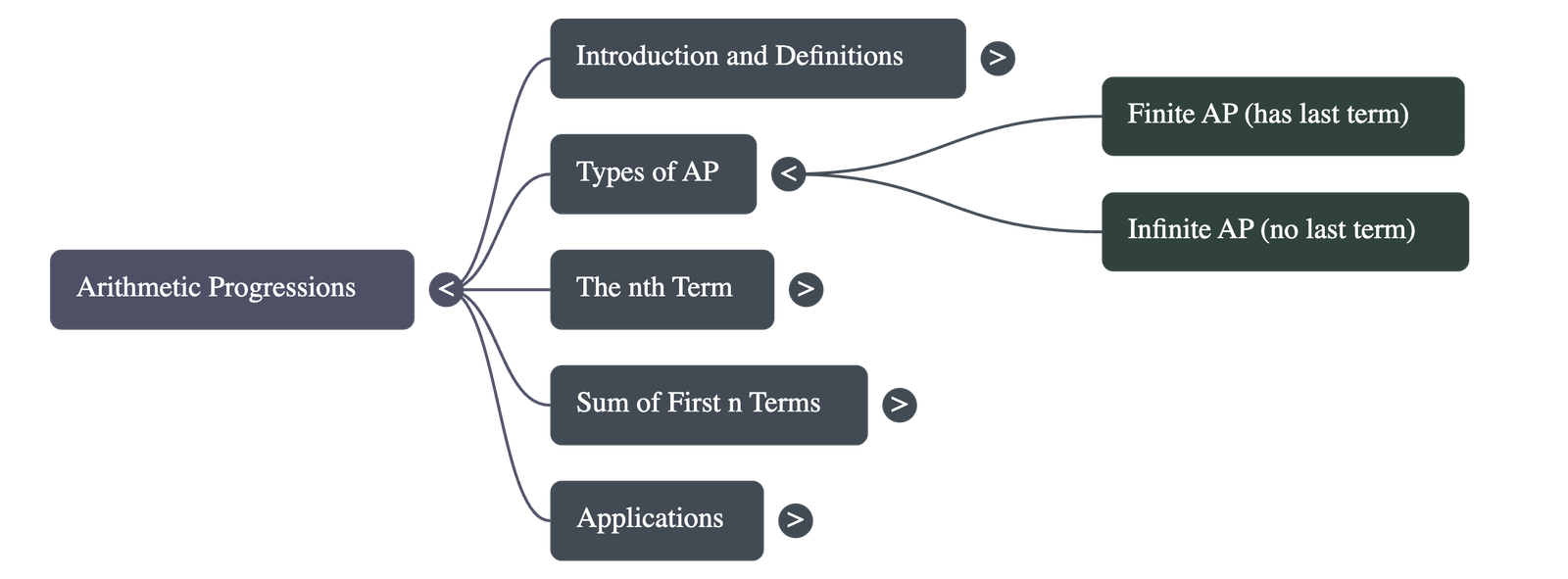
Types of APs:

• Finite AP: Contains a finite number of terms and has a specific last term.
• Infinite AP: Contains an infinite number of terms and has no last term.

Checking for an AP:

• A list of numbers is an AP if the difference between any two consecutive terms is the same.
• Formula check: a_k+1 – a_k is constant for all values of k.

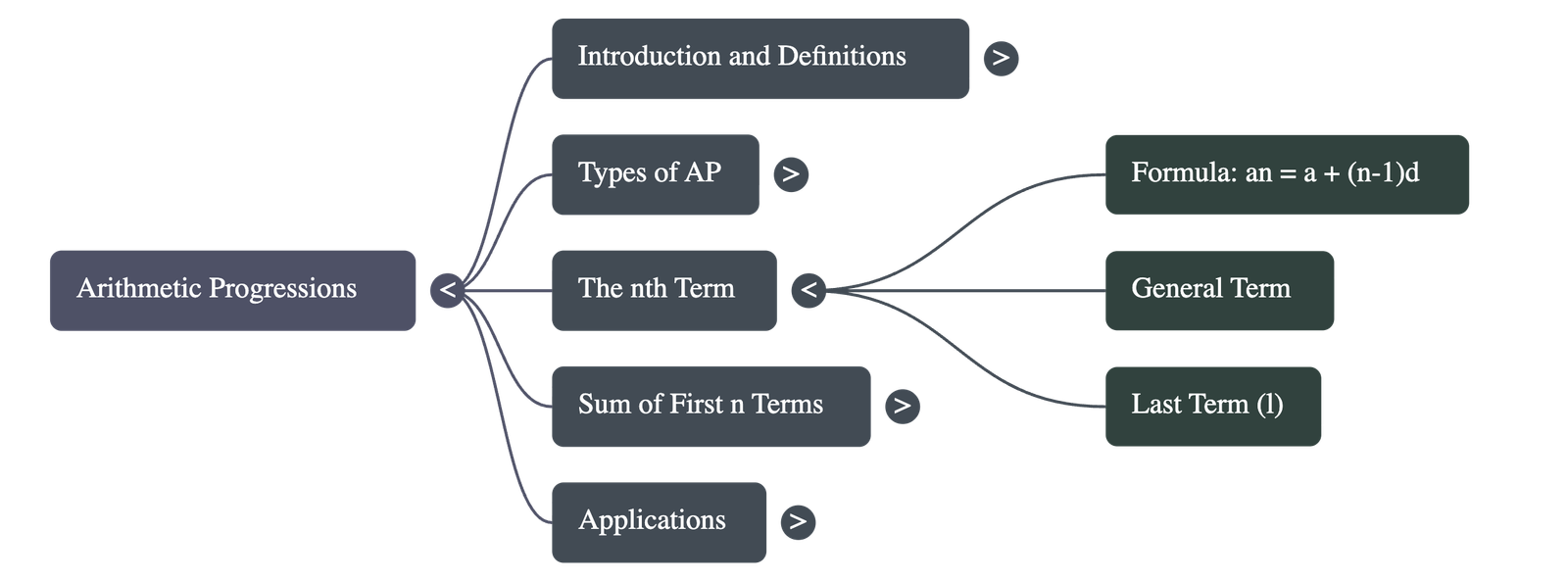
3. The nth Term of an AP

To find a specific term in a progression without listing all previous numbers, we use the general term formula.

• a_n: The nth term (or general term).
• a: The first term.
• d: The common difference.
• n: The position of the term.
• If an AP has m terms, a_m represents the last term, often denoted by l.

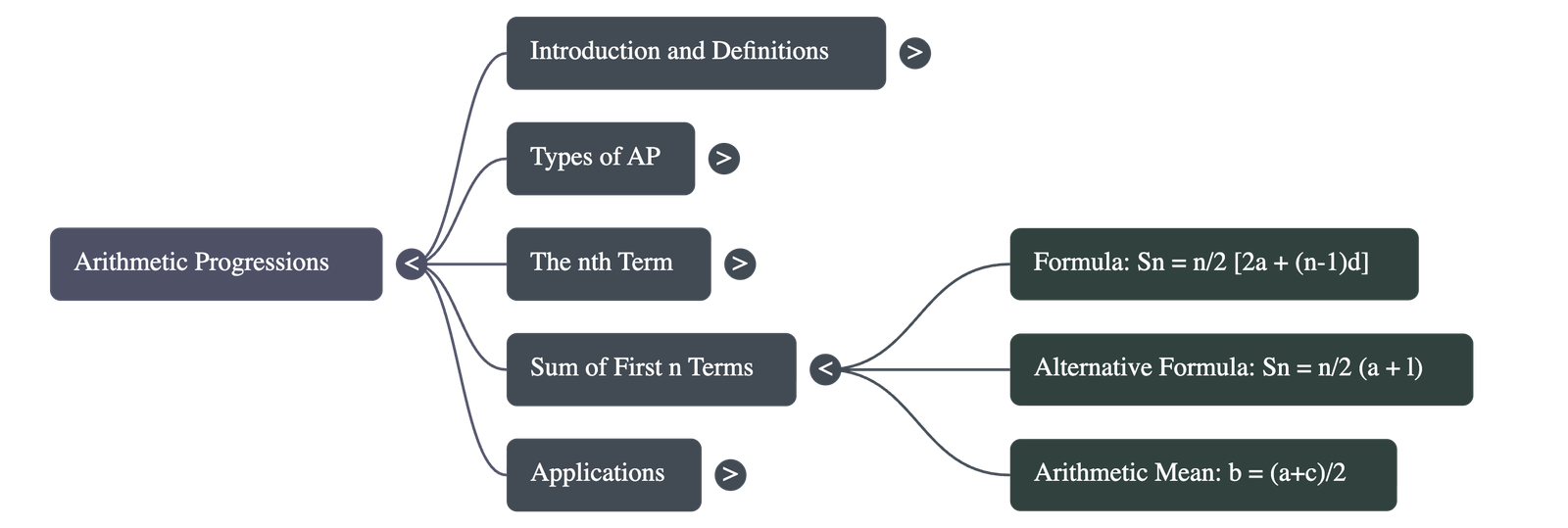
4. Sum of First n Terms of an AP

Instead of adding terms manually, specific formulas can be used to calculate the sum of the first n terms (denoted as S).

Primary Formula:

Alternative Formula (using last term):

If the first term (a) and the last term (l) are known:

Important Properties:

• Sum of first n positive integers:
  S_n = ^{n(n + 1)}⁄₂
• Finding the nth term from the Sum:
  The nth term is the difference between the sum of the first n terms and the sum of the first n-1 terms:
  a_n = S_n – S_n-1

5. Arithmetic Mean

A useful property for three numbers in an Arithmetic Progression:

• If a, b, c are in AP, then b is the arithmetic mean of a and c, given by:
  
  b = ^{(a + c)}⁄₂