Quick Navigation:
| | |
Triangles
1. Introduction
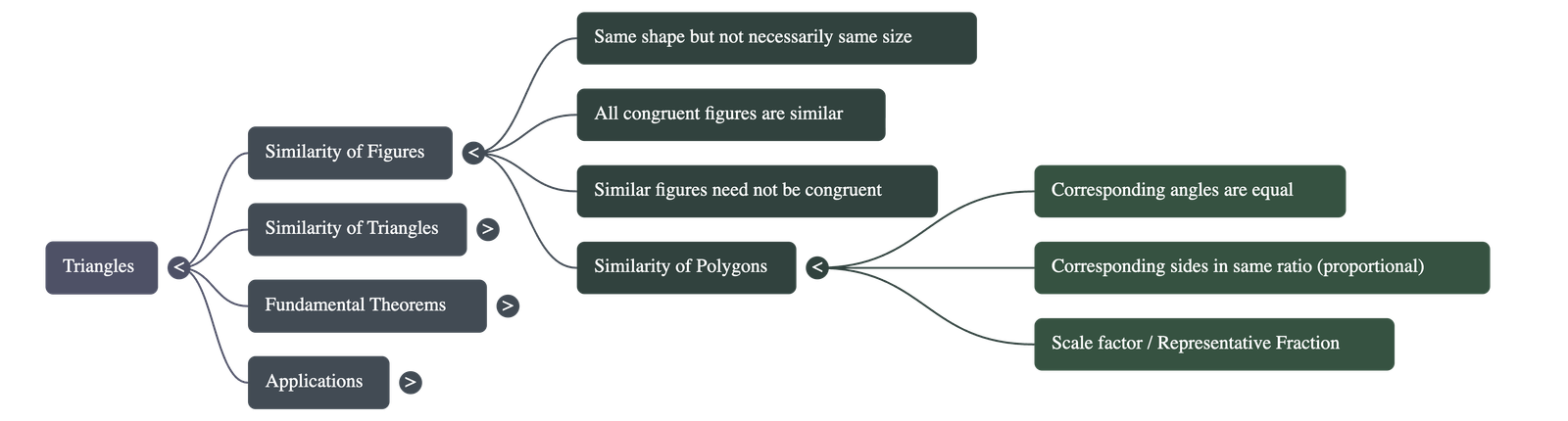
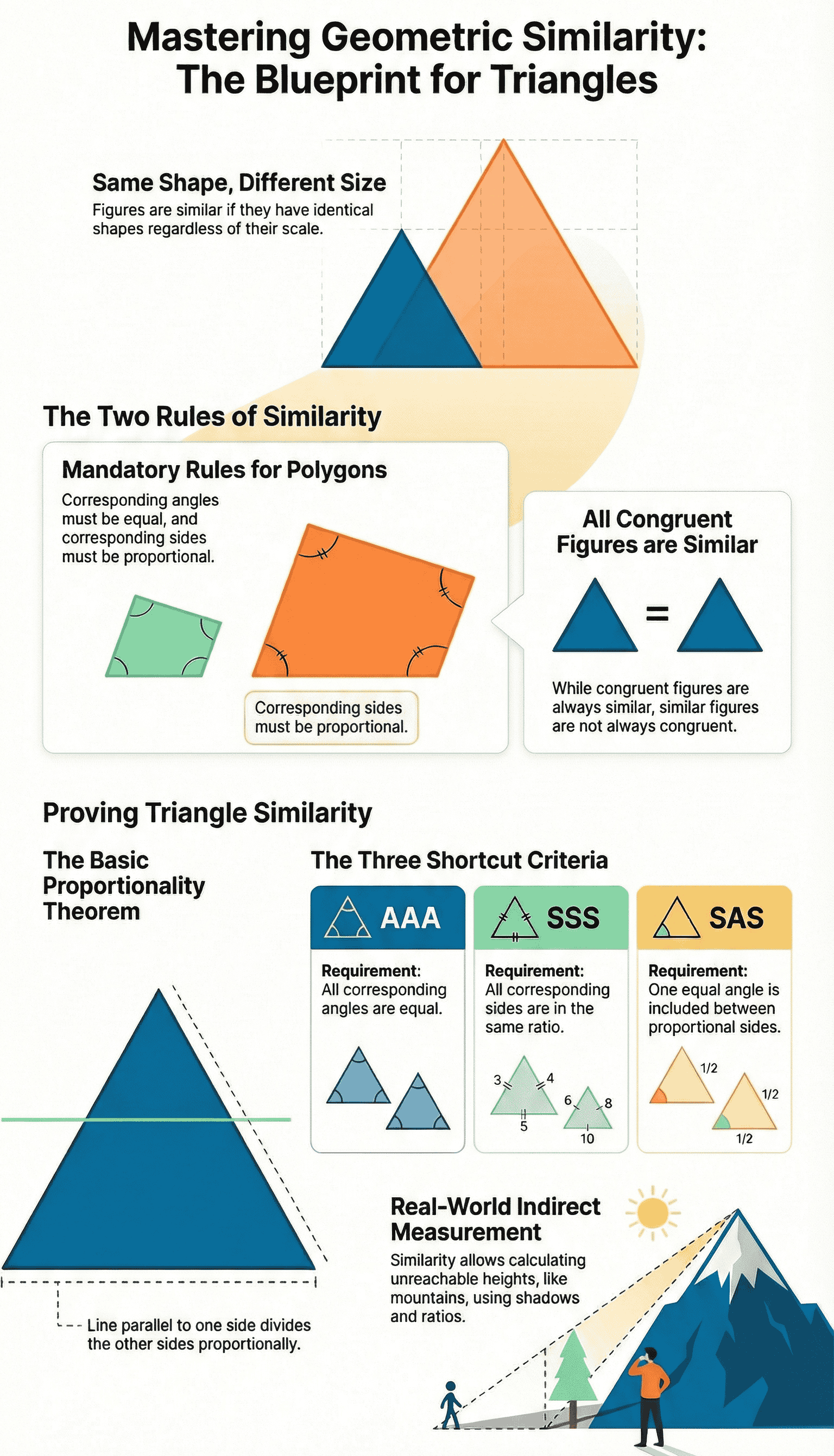
- Congruence vs. Similarity: Two figures are said to be congruent if they have the same shape and the same size. Figures that have the same shape but not necessarily the same size are called similar figures.
- Relationship: All congruent figures are similar, but similar figures need not be congruent.
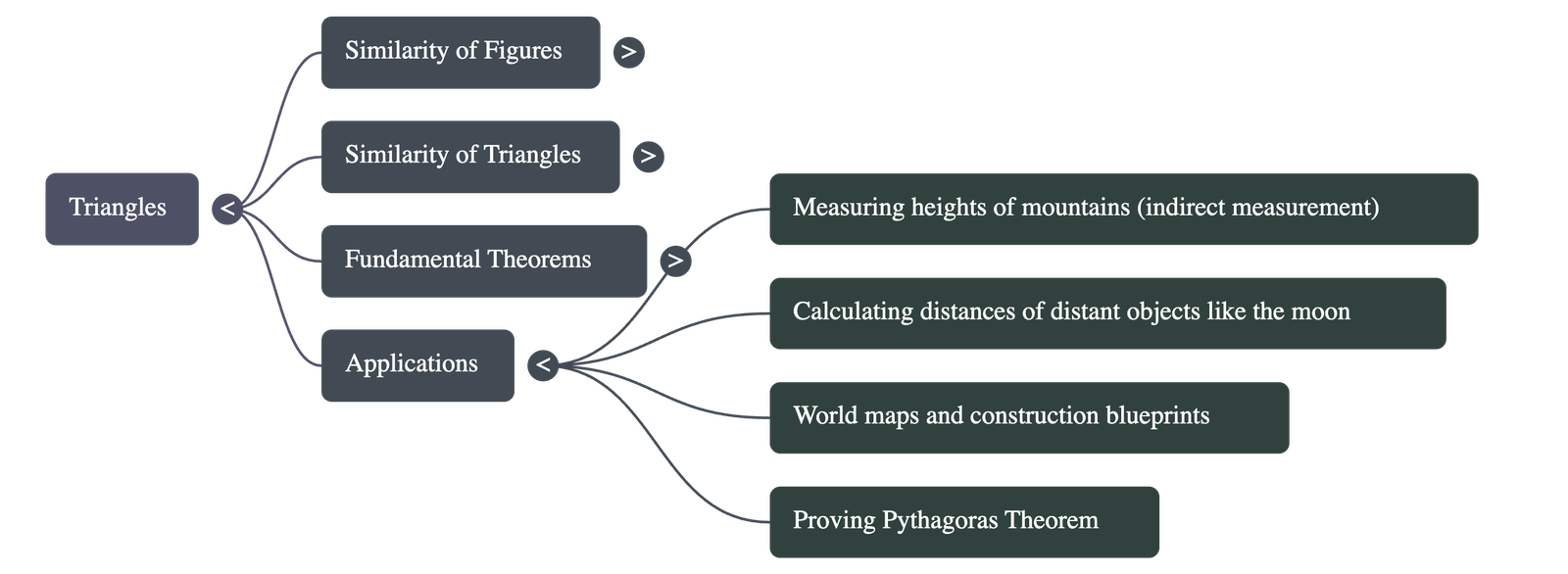
- Indirect Measurement: The principle of similarity is used for indirect measurements, such as finding the height of mountains or distances of long-distant objects like the moon.
2. Similar Figures
- Common Examples:
- All circles are similar.
- All squares are similar.
- All equilateral triangles are similar.
- Rules for Polygons: Two polygons of the same number of sides are similar if:
- Their corresponding angles are equal.
- Their corresponding sides are in the same ratio (or proportion).
- Scale Factor: The ratio of corresponding sides is referred to as the scale factor (or Representative Fraction). This concept is widely used in maps and blueprints.
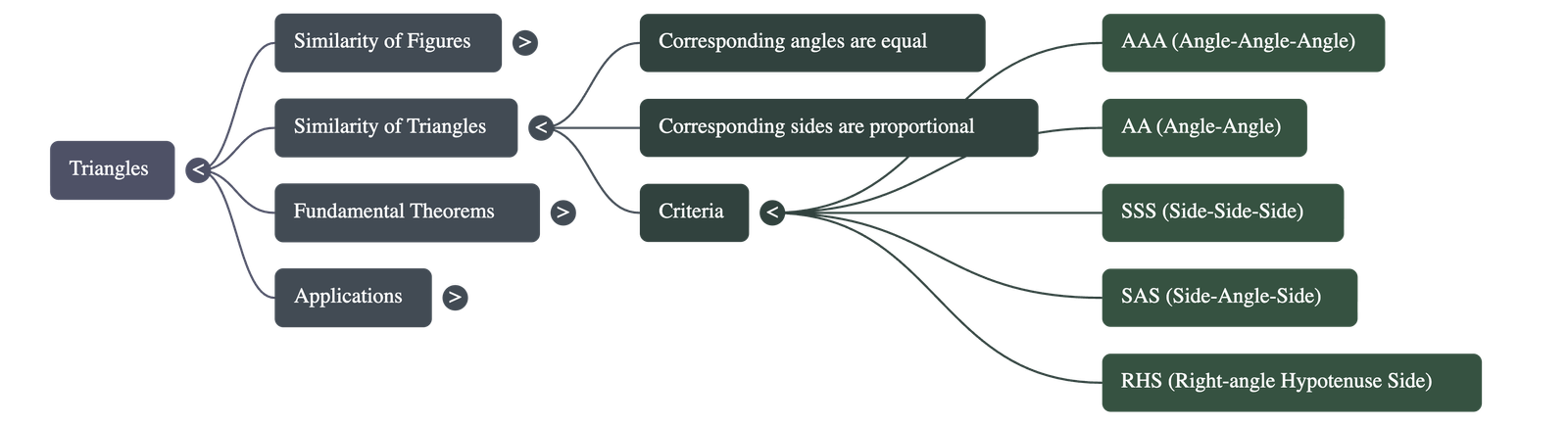
3. Similarity of Triangles
Two triangles are similar if:
- Their corresponding angles are equal (making them equiangular triangles).
- Their corresponding sides are in the same ratio (proportion).
Historical Note: The Greek mathematician Thales utilized the property that the ratio of any two corresponding sides in two equiangular triangles is always the same.
4. Basic Proportionality Theorem (Thales Theorem)
- Theorem 6.1: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
- Theorem 6.2 (Converse): If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
5. Criteria for Similarity of Triangles
It is not necessary to check all conditions (angles and sides) to prove similarity. The following criteria are sufficient:
A. AAA (Angle-Angle-Angle) Similarity
- Theorem 6.3: If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio, and hence the two triangles are similar.
- AA Similarity: If two angles of one triangle are respectively equal to two angles of another triangle, the triangles are similar (since the third angle must also be equal).
B. SSS (Side-Side-Side) Similarity
- Theorem 6.4: If in two triangles, sides of one triangle are proportional to the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar.
C. SAS (Side-Angle-Side) Similarity
- Theorem 6.5: If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
Special Note on RHS Similarity
If in two right triangles, the hypotenuse and one side of one triangle are proportional to the hypotenuse and one side of the other triangle, then the two triangles are similar.
6. Summary of Key Theorems
- A line parallel to one side of a triangle divides the other two sides proportionally.
- A line dividing two sides of a triangle proportionally is parallel to the third side.
- Triangles are similar if corresponding angles are equal (AAA).
- Triangles are similar if corresponding sides are proportional (SSS).
- Triangles are similar if one angle is equal and the including sides are proportional (SAS).
Quick Navigation:
| | |
1 / 1
Quick Navigation:
| | |