Q&A & Flashcards Available

Access questions, answers and flashcards for this chapter

View Q&A
Infographic
Quick Navigation:
| | |

CHAPTER 2: POLYNOMIALS

1. Introduction to Polynomials in One Variable

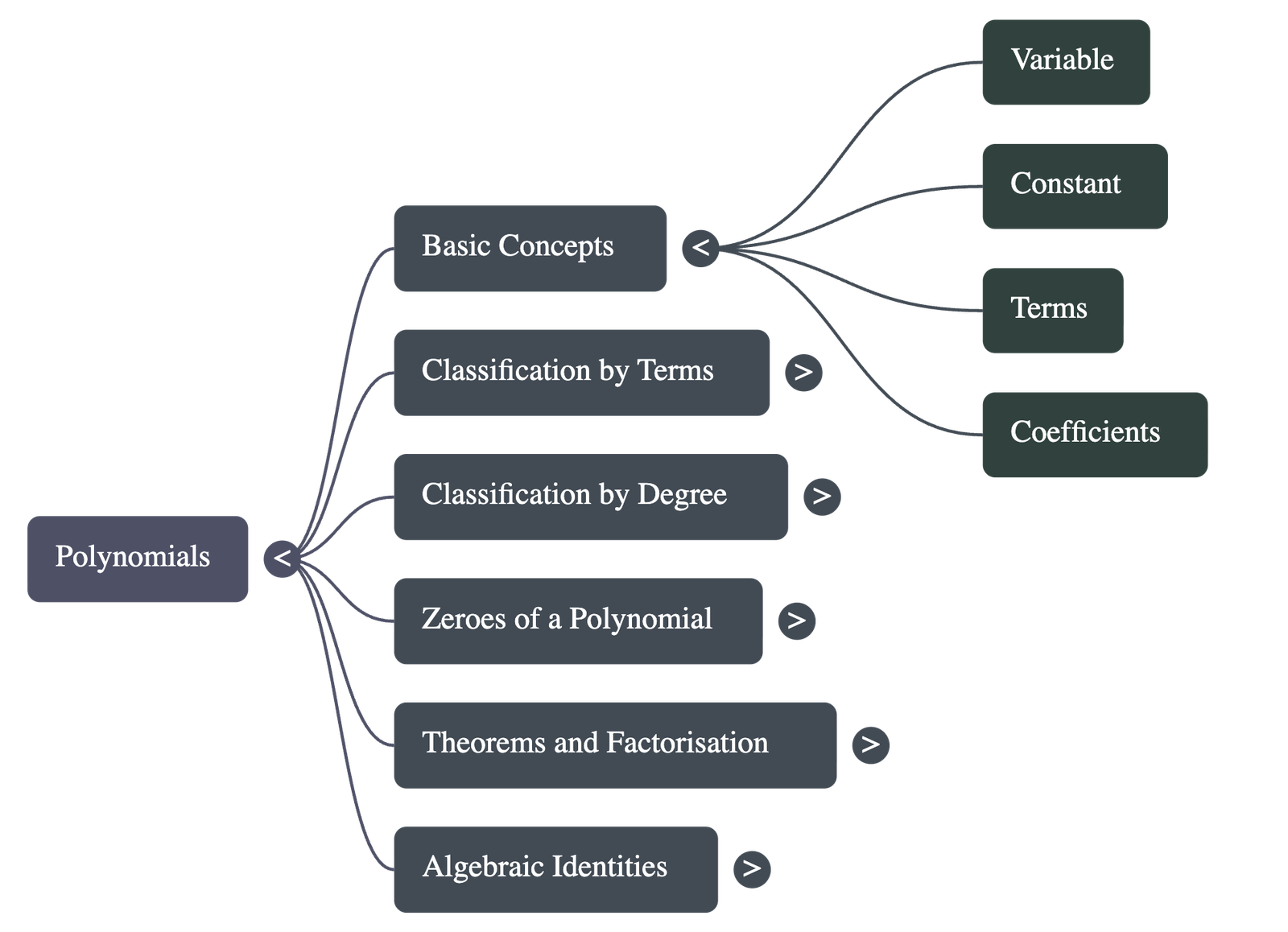
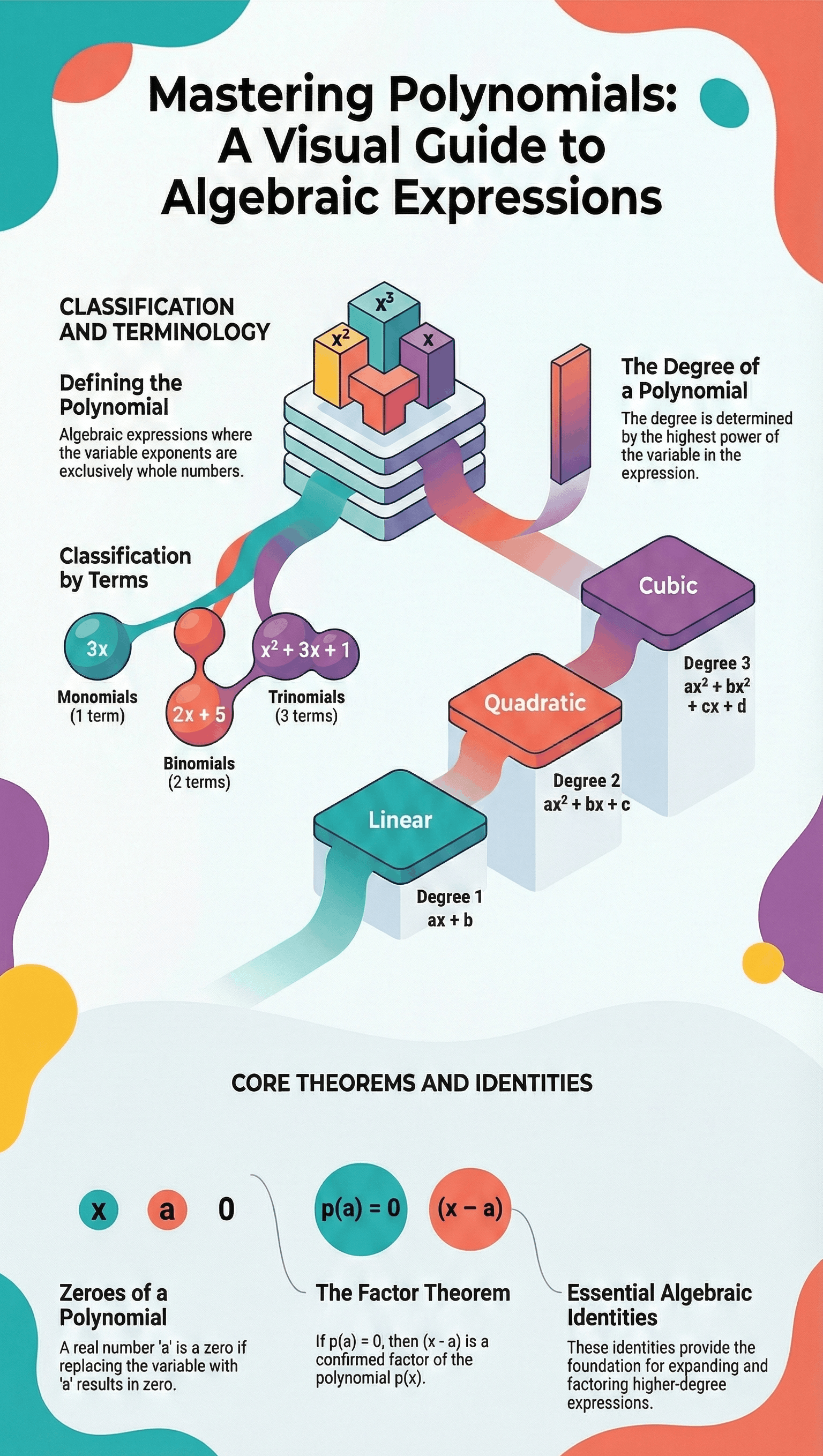
  • Definition: A polynomial in one variable (usually denoted as x) is an algebraic expression where the exponents of the variable are always whole numbers (non-negative integers).
  • Terms: The parts of the polynomial separated by addition or subtraction are called terms. For example, in x2 + 2x, the terms are x2 and 2x.
  • Coefficients: Each term has a coefficient. For example, in -x3 + 4x2, the coefficient of x3 is -1 and the coefficient of x2 is 4.
  • Constants: Numbers like 2, -5, and 7 are called constant polynomials. The constant polynomial 0 is specifically called the zero polynomial.
  • Notation: Polynomials are often denoted by symbols such as p(x), q(x), or r(y).

2. Classification of Polynomials

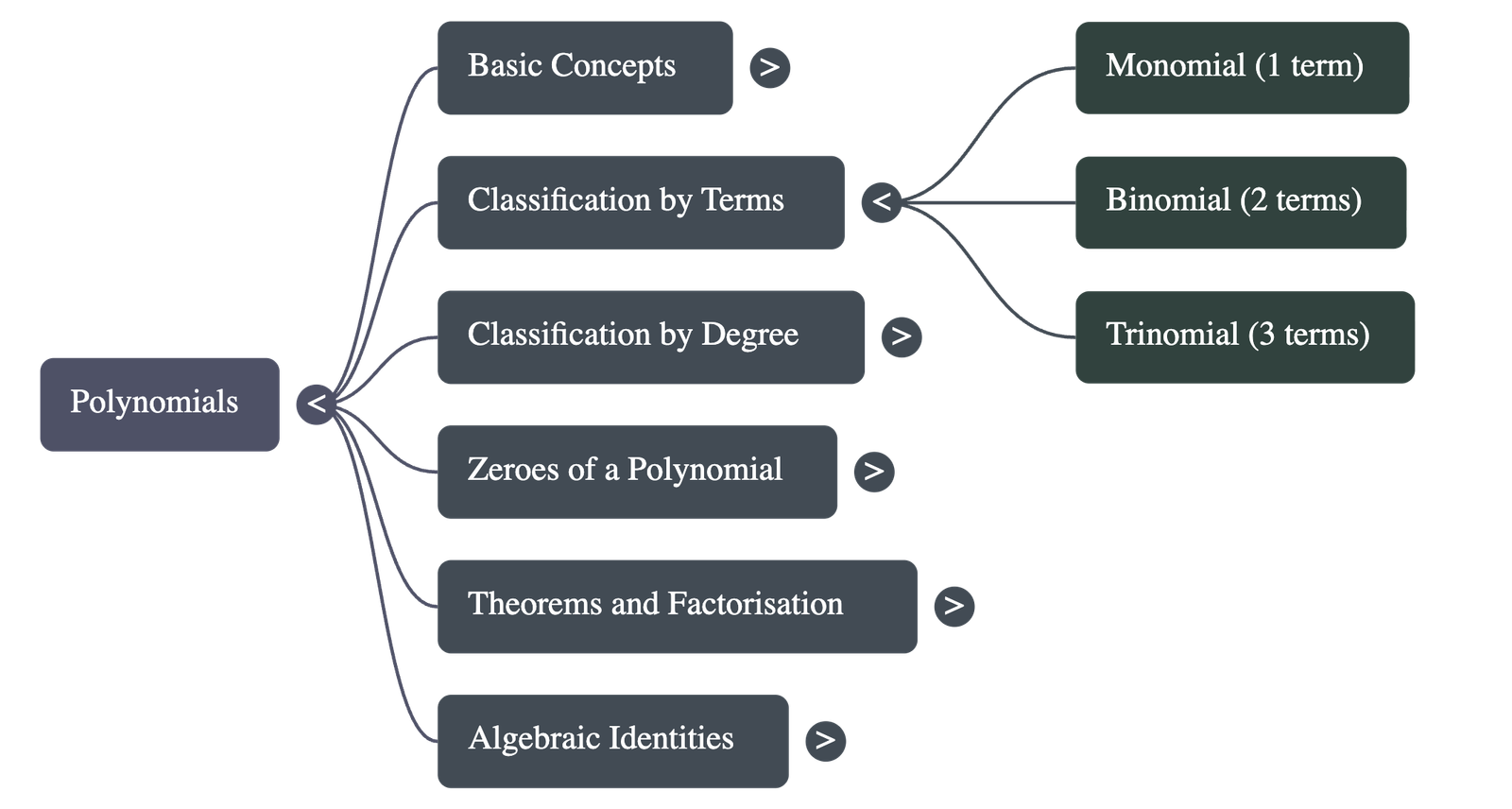
By Number of Terms

  • Monomial: A polynomial having only one term (e.g., 2x, 5x3).
  • Binomial: A polynomial having only two terms (e.g., x + 1, x2 - x).
  • Trinomial: A polynomial having only three terms (e.g., x2 + x + π).

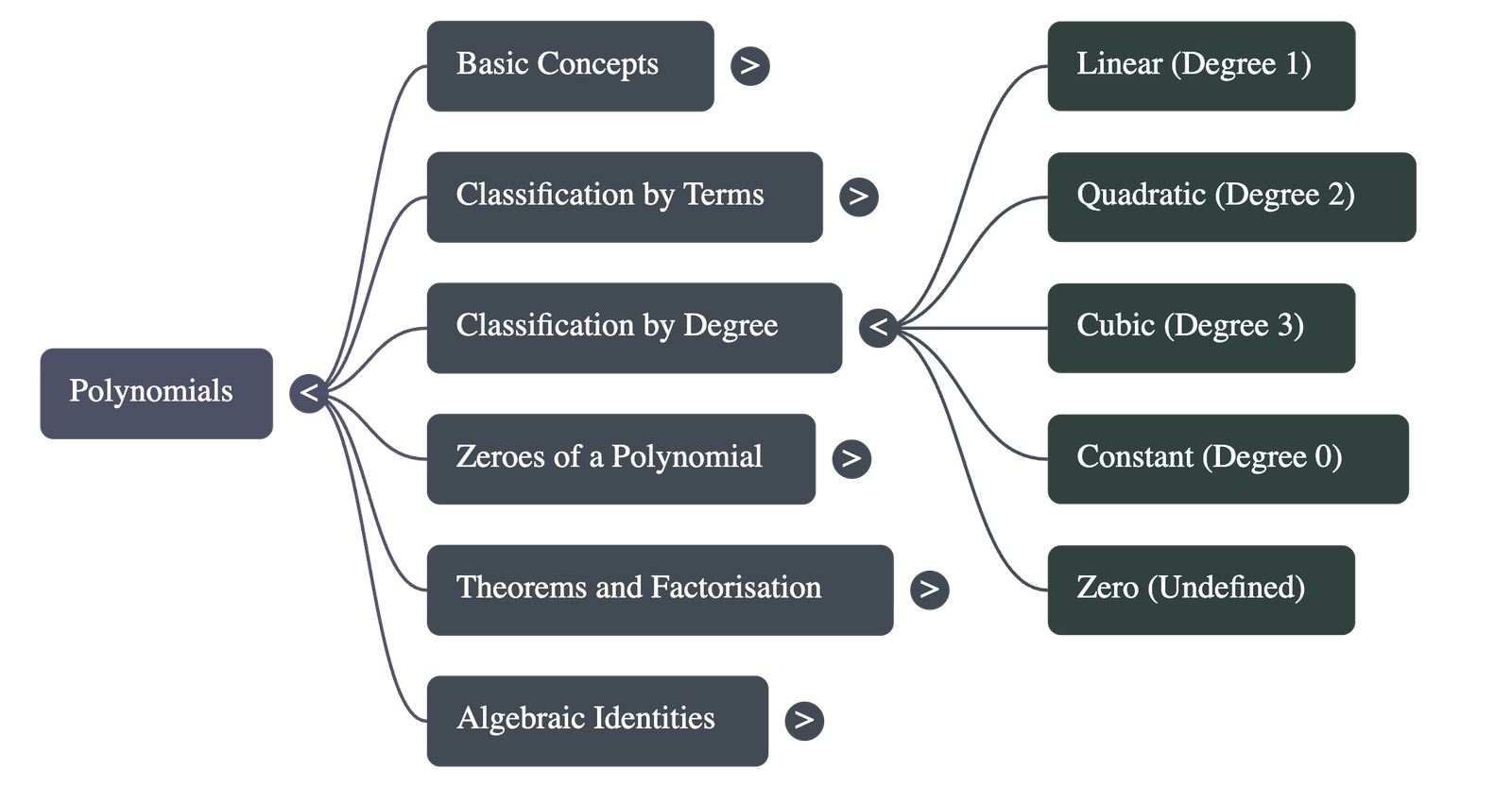
By Degree (Highest Power)

The degree of a polynomial is the highest power of the variable appearing in the polynomial.

  • Linear Polynomial: A polynomial of degree 1. The general form is ax + b (where a ≠ 0). It has at most two terms.
  • Quadratic Polynomial: A polynomial of degree 2. The general form is ax2 + bx + c (where a ≠ 0). It has at most three terms.
  • Cubic Polynomial: A polynomial of degree 3. The general form is ax3 + bx2 + cx + d (where a ≠ 0). It has at most four terms.
  • Note on Constants: The degree of a non-zero constant polynomial is 0. The degree of the zero polynomial is not defined.

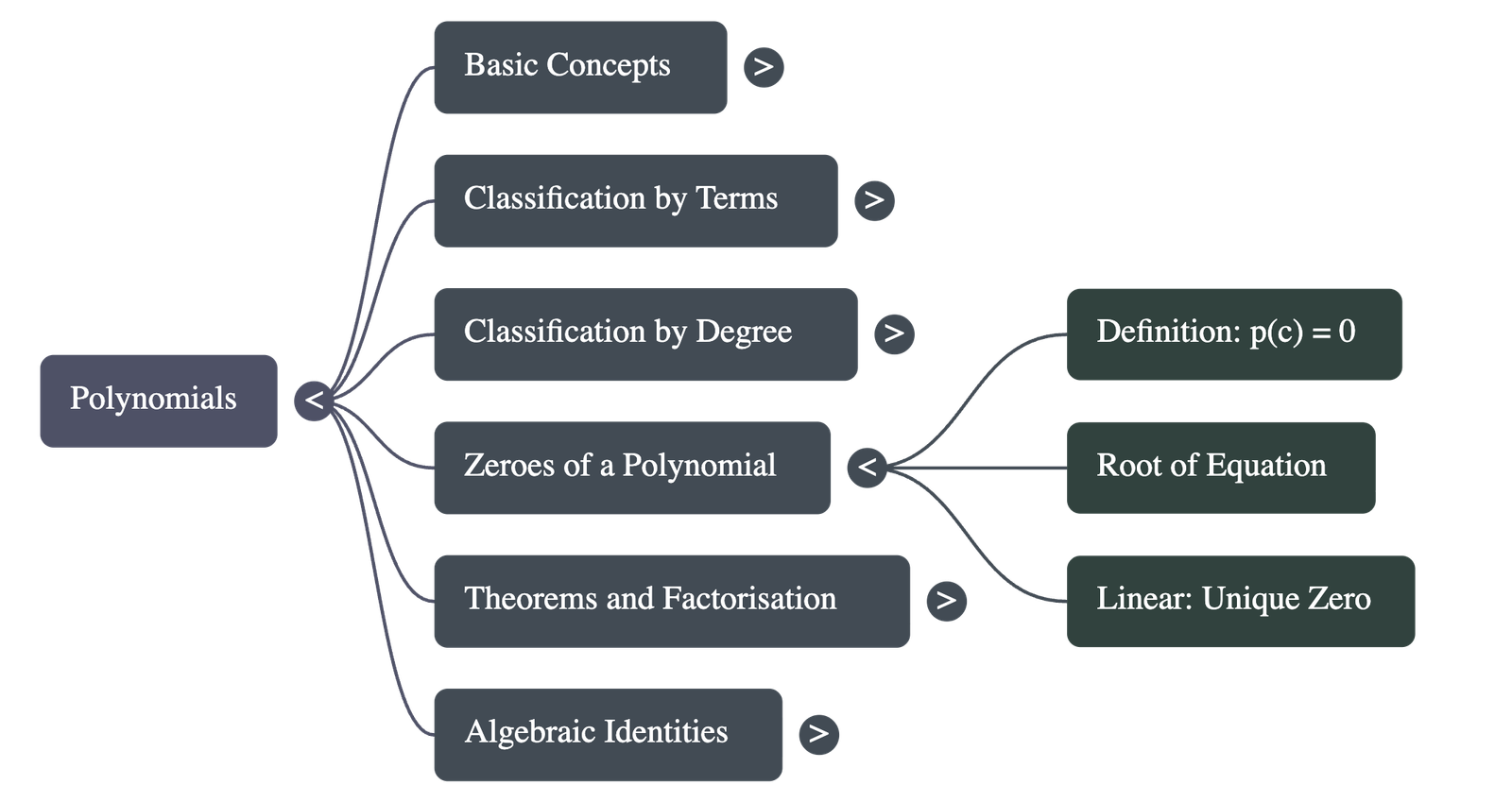
3. Zeroes of a Polynomial

  • Definition: A real number c is a zero of a polynomial p(x) if p(c) = 0.
  • Roots: If c is a zero of p(x), then c is also called a root of the polynomial equation p(x) = 0.
  • Finding Zeroes: Finding a zero amounts to solving the equation p(x) = 0.
  • Properties:
    • A zero of a polynomial need not be the number 0.
    • 0 may be a zero of a polynomial.
    • Every linear polynomial has one and only one zero.
    • A polynomial can have more than one zero.
    • A non-zero constant polynomial has no zero.
    • By convention, every real number is a zero of the zero polynomial.

4. Factorisation of Polynomials

  • Factor Theorem: If p(x) is a polynomial of degree n > 1 and a is any real number, then:
    1. (x - a) is a factor of p(x) if p(a) = 0.
    2. p(a) = 0 if (x - a) is a factor of p(x).
  • Factorising Quadratics (Splitting the Middle Term): To factorise ax2 + bx + c, we find two numbers whose sum is b and whose product is ac.
  • Factorising Cubics: Often involves finding one factor using the Factor Theorem (by trial) and then dividing the polynomial to solve the remaining quadratic part.

5. Algebraic Identities

The chapter details several key algebraic identities used for factorisation and evaluating expressions:

  • Identity I: (x + y)2 = x2 + 2xy + y2
  • Identity II: (x - y)2 = x2 - 2xy + y2
  • Identity III: x2 - y2 = (x + y)(x - y)
  • Identity IV: (x + a)(x + b) = x2 + (a + b)x + ab
  • Identity V: (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx
  • Identity VI: (x + y)3 = x3 + y3 + 3xy(x + y)
  • Identity VII: (x - y)3 = x3 - y3 - 3xy(x - y)
  • Identity VIII: x3 + y3 + z3 - 3xyz = (x + y + z)(x2 + y2 + z2 - xy - yz - zx)
  • Note: Identity VIII simplifies significantly if x + y + z = 0, resulting in x3 + y3 + z3 = 3xyz.
Quick Navigation:
| | |
1 / 1
Quick Navigation:
| | |
Quick Navigation:
| | |