Quick Navigation:
| | |
CHAPTER 3: COORDINATE GEOMETRY
1. Introduction to Coordinate Geometry
- To locate the position of an object or a point precisely in a plane, a single reference point is insufficient. We require two independent pieces of information or references.
- Real-life examples:
- Finding a house usually requires a Street Number and a House Number.
- Describing a seating plan requires a Column Number and a Row Number.
- This system of geometry was initially developed by the French philosopher and mathematician René Descartes. The system used for describing the position of a point in a plane is called the Cartesian system in his honour.
2. The Cartesian System
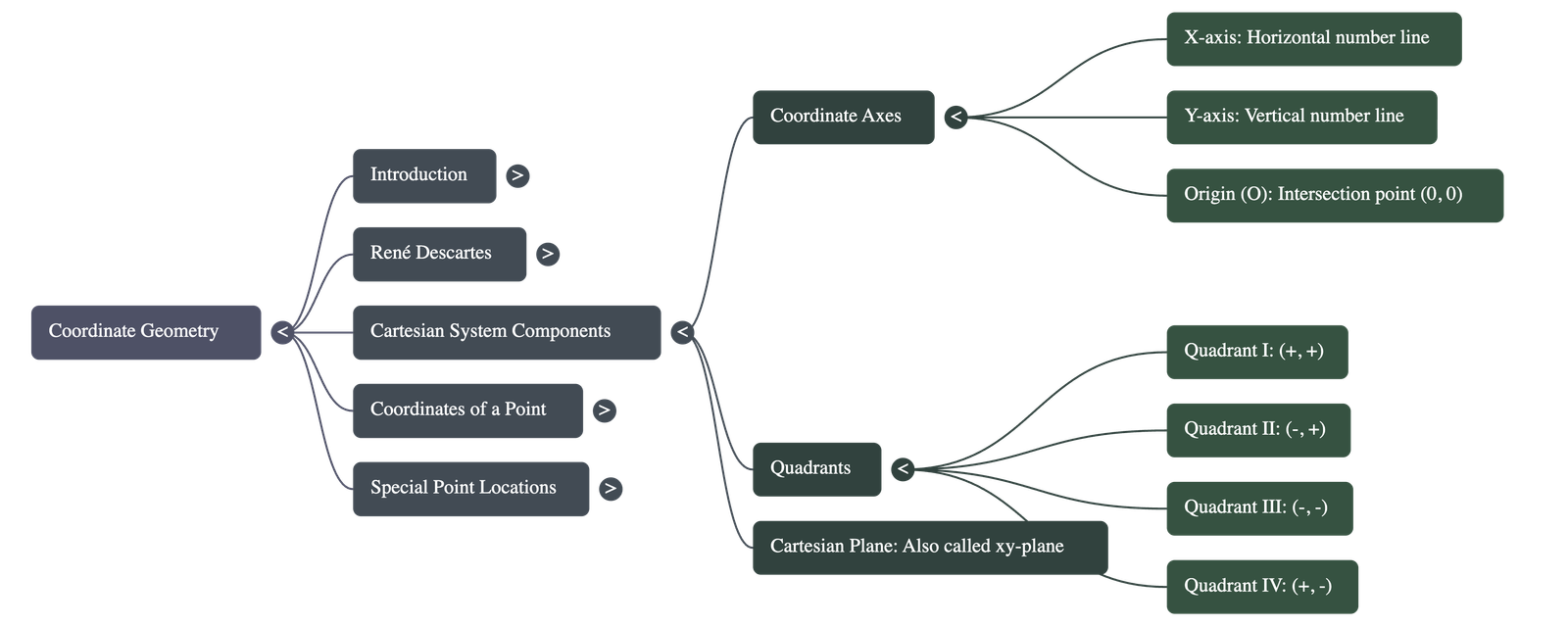
The system is based on two perpendicular number lines intersecting each other.
- Coordinate Axes:
- The horizontal number line is called the x-axis (denoted as X'X).
- The vertical number line is called the y-axis (denoted as Y'Y).
- The Origin: The point where the two axes intersect is called the origin and is denoted by the letter O.
- Direction:
- OX and OY represent the positive directions (positive numbers).
- OX' and OY' represent the negative directions (negative numbers).
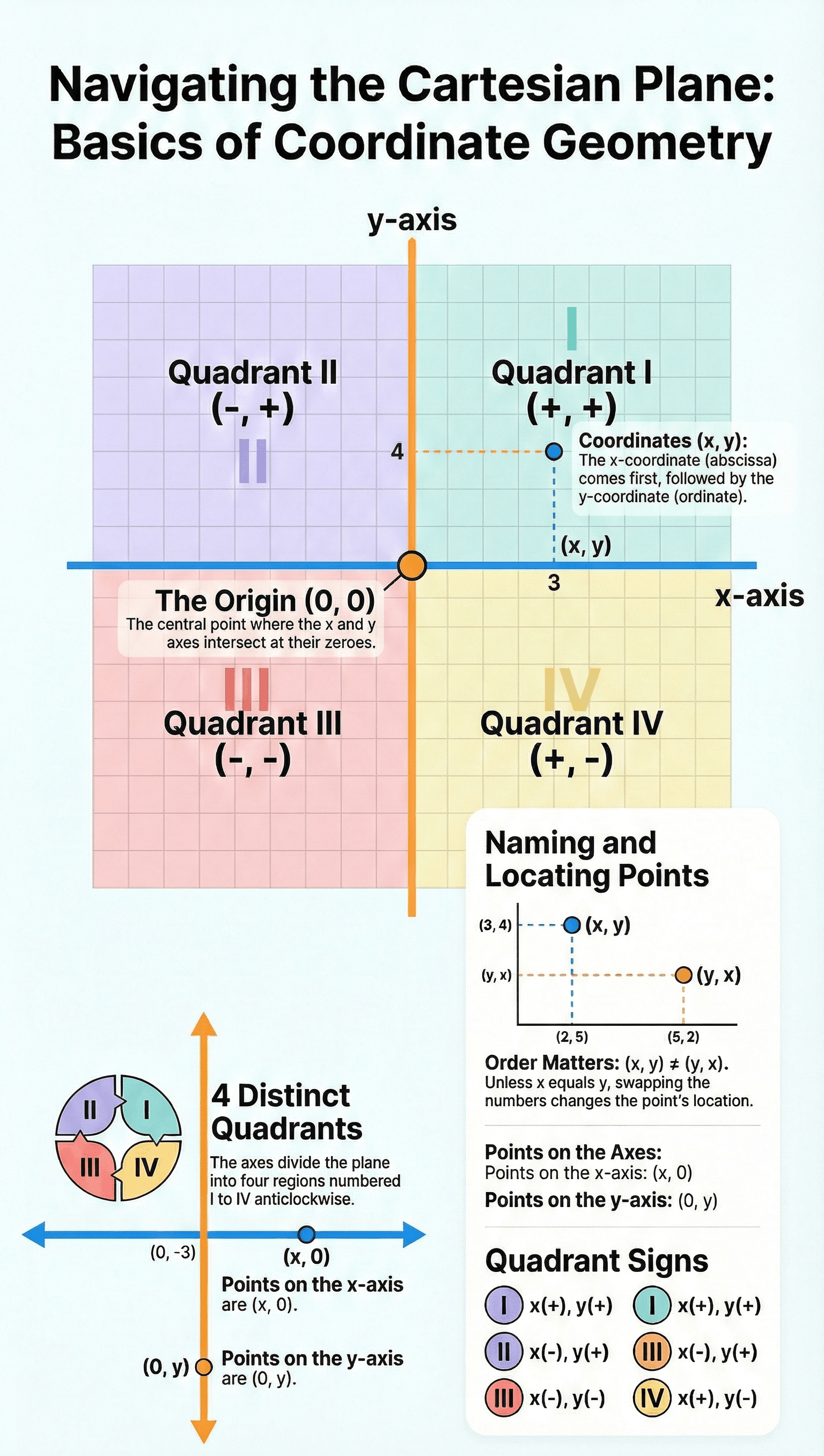
- Quadrants: The axes divide the plane into four distinct parts called quadrants. They are numbered anticlockwise starting from the positive x-axis:
- Quadrant I: Enclosed by positive x-axis and positive y-axis.
- Quadrant II: Enclosed by negative x-axis and positive y-axis.
- Quadrant III: Enclosed by negative x-axis and negative y-axis.
- Quadrant IV: Enclosed by positive x-axis and negative y-axis.
- The entire plane is referred to as the Cartesian plane, the coordinate plane, or the xy-plane.
3. Coordinates of a Point
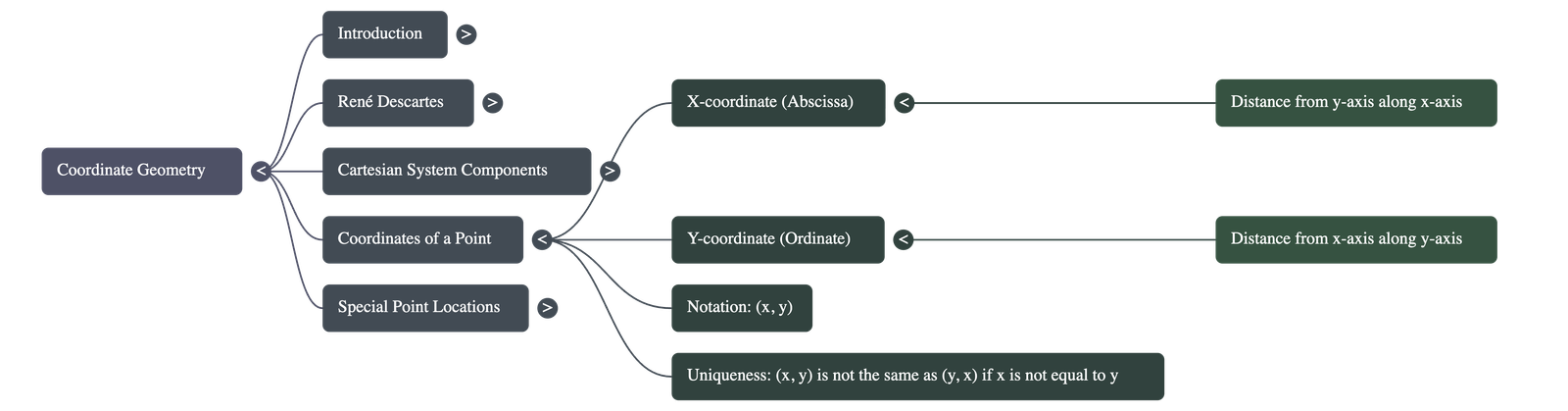
The position of a point is defined by its distances from the axes.
- Abscissa (x-coordinate): The perpendicular distance of a point from the y-axis (measured along the x-axis).
(Positive along the positive direction of the x-axis and negative along the negative direction). - Ordinate (y-coordinate): The perpendicular distance of a point from the x-axis (measured along the y-axis).
(Positive along the positive direction of the y-axis and negative along the negative direction). - Notation: The coordinates of a point are written in brackets as (x, y), where the x-coordinate comes first, followed by the y-coordinate.
- Uniqueness: The order matters. For example, (3, 4) is not the same position as (4, 3). Generally, if x ≠ y, then (x, y) ≠ (y, x).
4. Specific Points and Sign Conventions
| Location of Point | Coordinate Format | Sign Convention |
|---|---|---|
| Quadrant I | (x, y) | (+, +) |
| Quadrant II | (x, y) | (−, +) |
| Quadrant III | (x, y) | (−, −) |
| Quadrant IV | (x, y) | (+, −) |
| On the x-axis | (x, 0) | Ordinate is always zero |
| On the y-axis | (0, y) | Abscissa is always zero |
| At the Origin | (0, 0) | Zero distance from both axes |
Quick Navigation:
| | |
1 / 1
Quick Navigation:
| | |