LINEAR EQUATIONS IN TWO VARIABLES

• Recall of One-Variable Equations In earlier studies, linear equations in one variable (e.g., x + 1 = 0) were introduced. These equations are characterized by having a unique (one and only one) solution that can be represented on a number line.
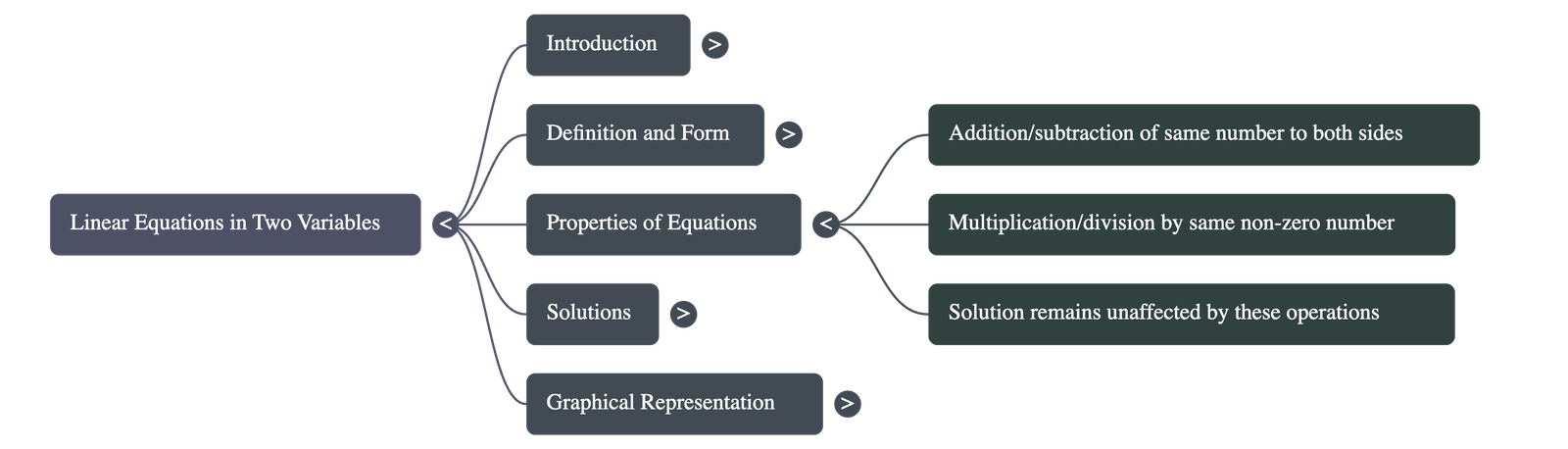
• Fundamental Solving Principles The solution of a linear equation remains unchanged when:
  • The same number is added to or subtracted from both sides.
  • Both sides are multiplied or divided by the same non-zero number.
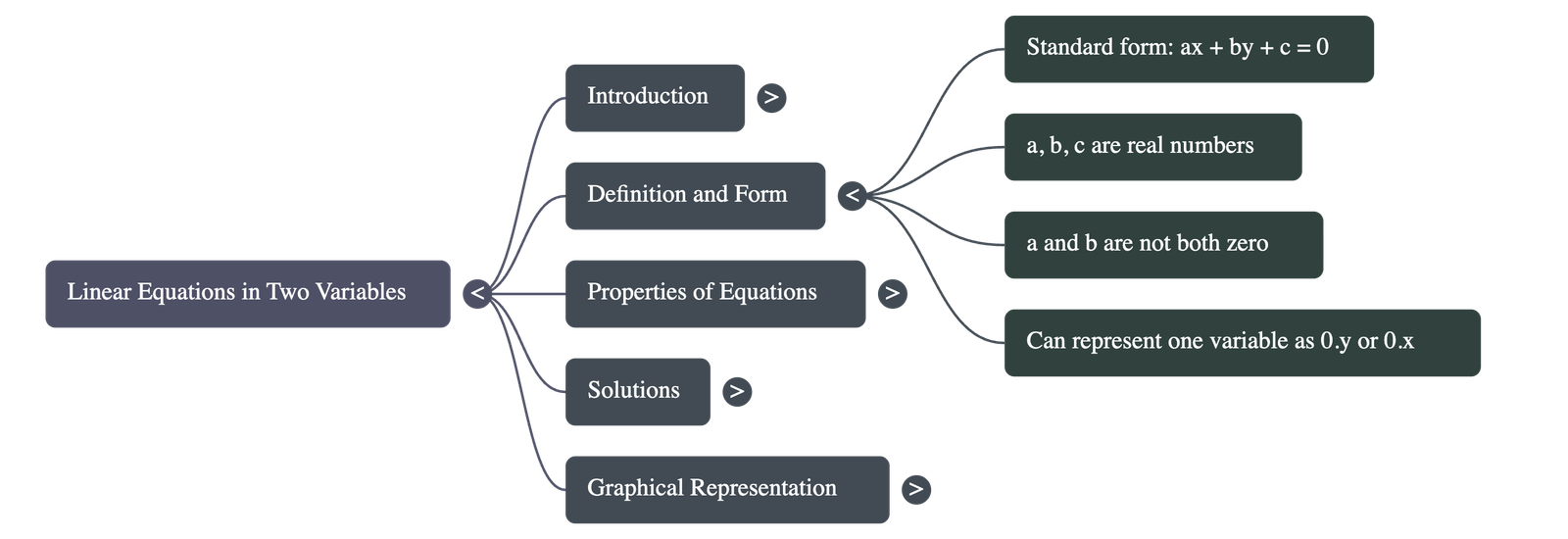
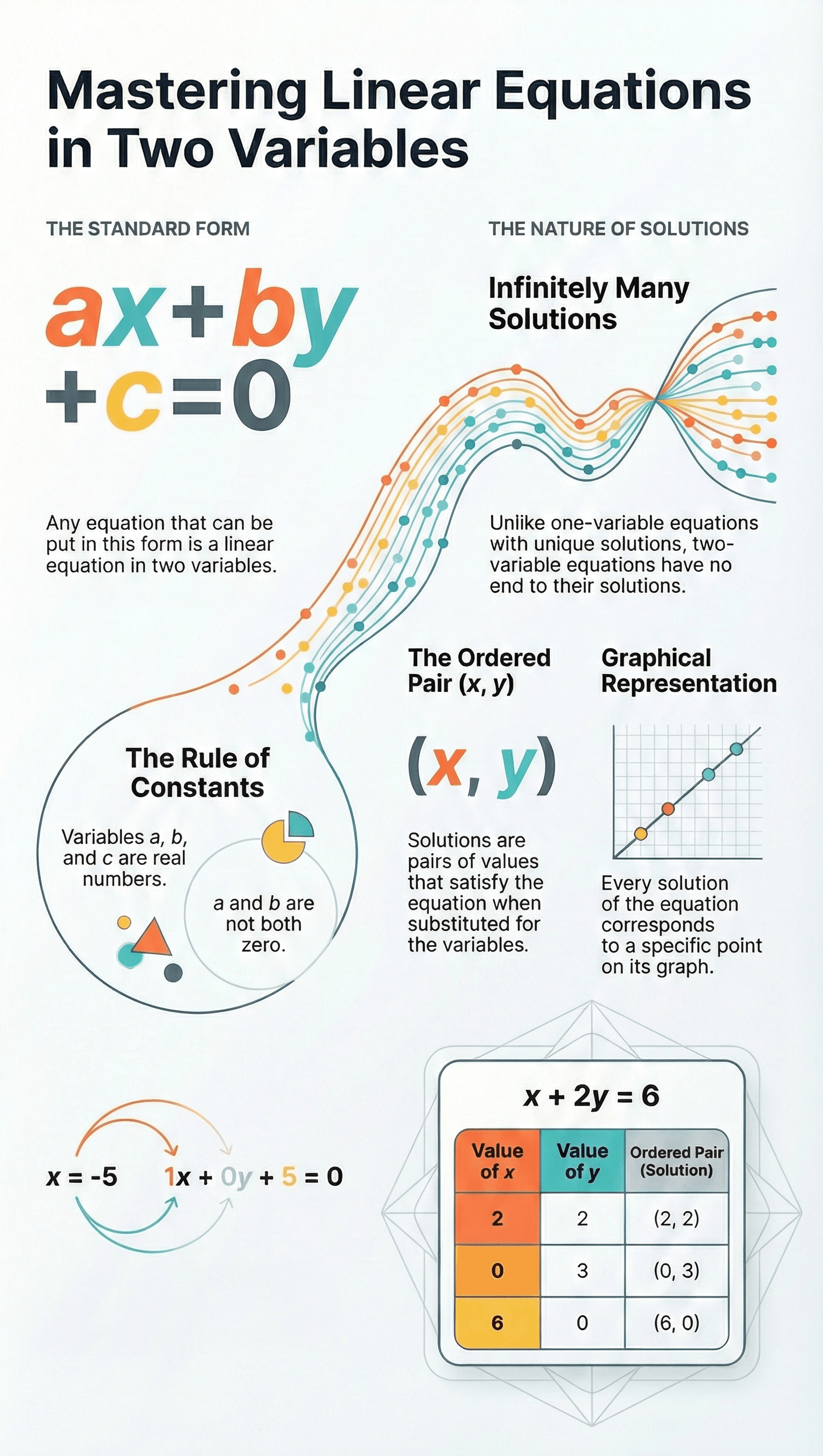
• Definition of Two-Variable Equations Any equation that can be expressed in the form ax + by + c = 0, where a, b, and c are real numbers and a and b are not both zero, is defined as a linear equation in two variables.
• Expressing One Variable as Two Equations typically seen as one-variable equations, such as x = -5 or y = 2, can also be expressed as linear equations in two variables. For instance, x = -5 can be written as 1x + 0y + 5 = 0.
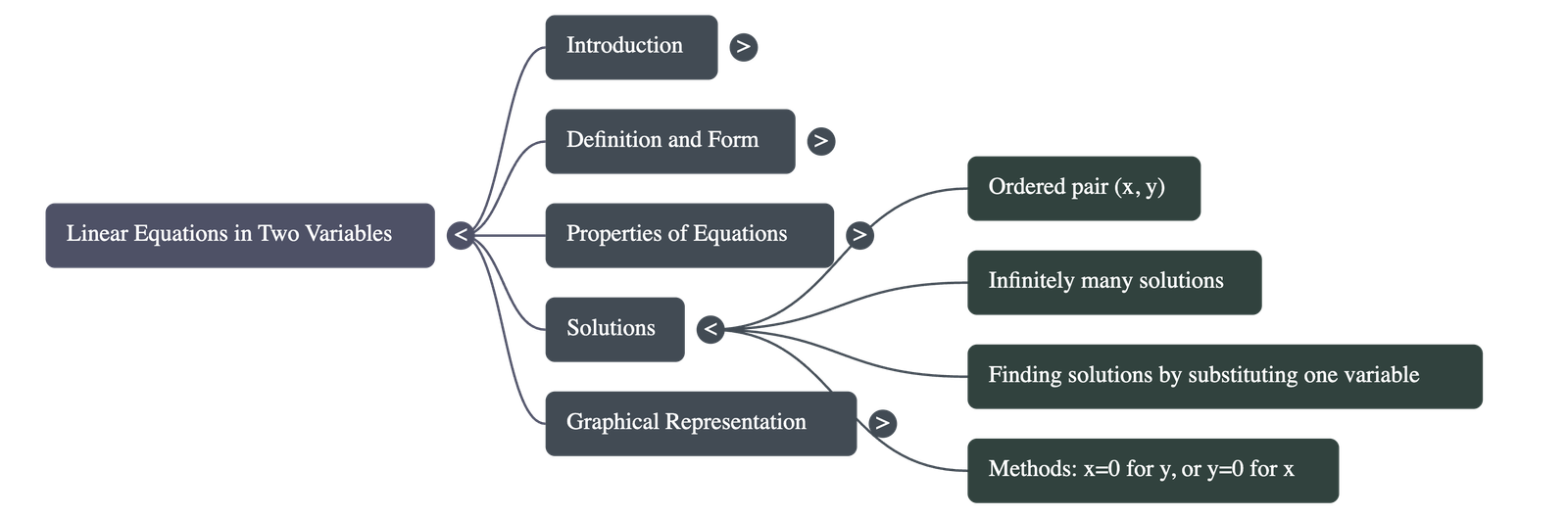
• Infinite Nature of Solutions Unlike equations in one variable, a linear equation in two variables has infinitely many solutions. Since there are two variables, a solution is represented as a pair of values—one for x and one for y—that satisfy the equation.
• Ordered Pairs Solutions are written as an ordered pair (x, y). For example, in the equation 2x + 3y = 12, the pair (3, 2) is a solution because substituting x=3 and y=2 makes the equation true. Note that the order matters: (0, 4) might be a solution while (4, 0) is not.
• Method for Finding Solutions A practical way to find solutions is to substitute a chosen value for one variable (e.g., let x = 0) and solve the resulting one-variable equation to find the corresponding value of the other variable (y).
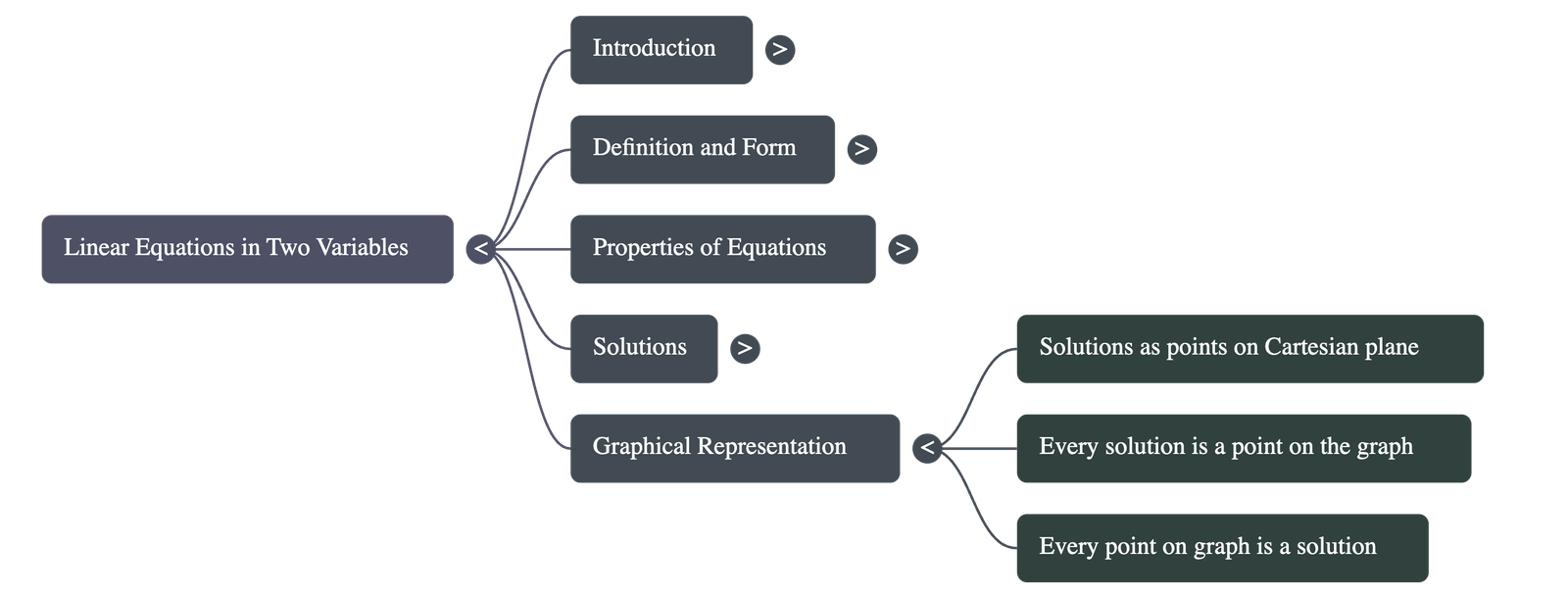
• Geometric Connection Every solution of a linear equation corresponds to a point on its graph in the Cartesian plane. Conversely, every point located on the graph of the equation is a valid solution for that equation.