Quick Navigation:
| | |
CHAPTER 9: CIRCLES
Fundamental Definitions
- Definition: A circle is the collection of all points in a plane that are equidistant from a fixed point in the plane.
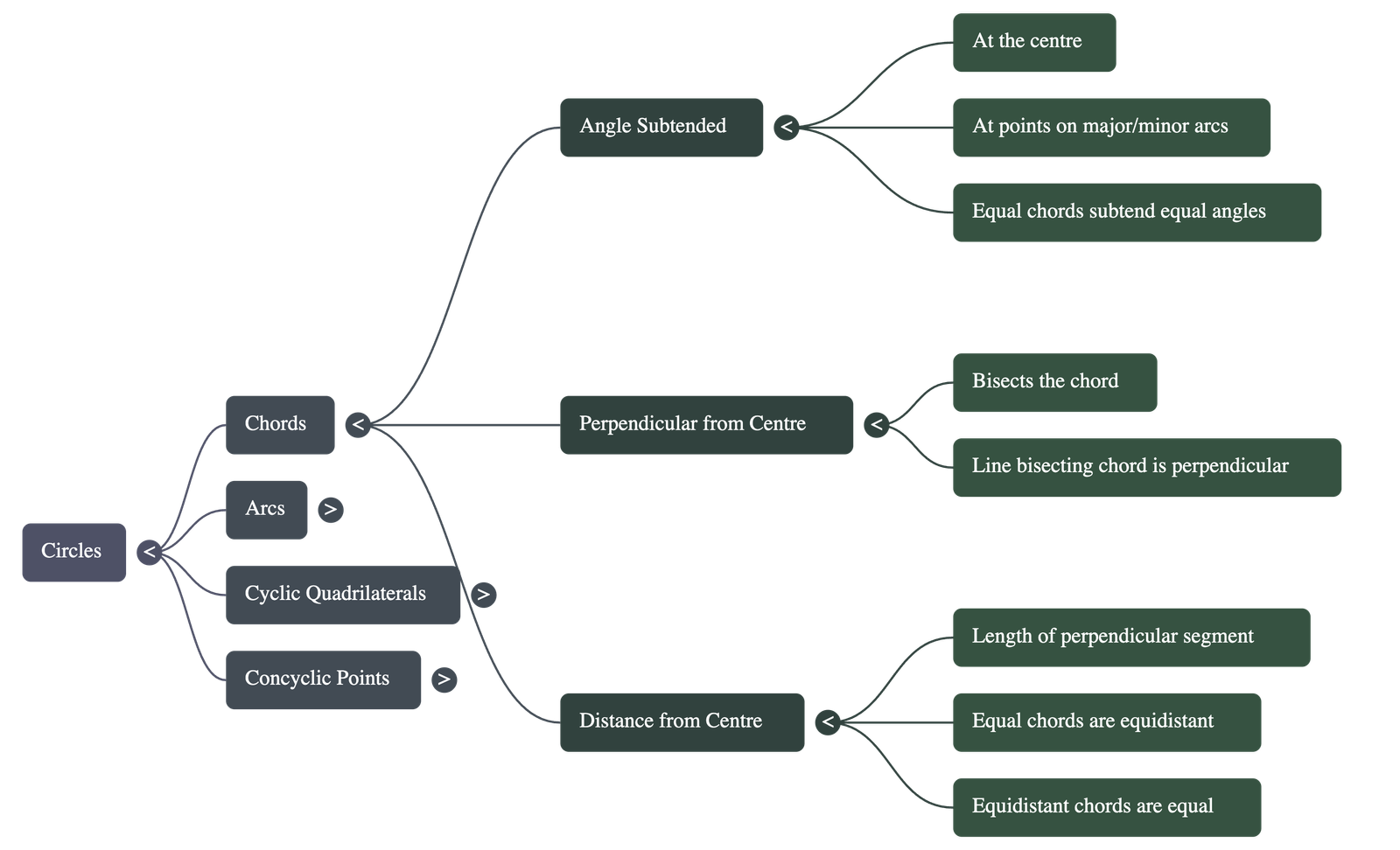
- Subtended Angles: An angle formed by joining the endpoints of a line segment to a point is called the angle subtended by that segment at that point. In a circle, this can occur at the centre, on the major arc, or on the minor arc.
Chords and Center Relationships
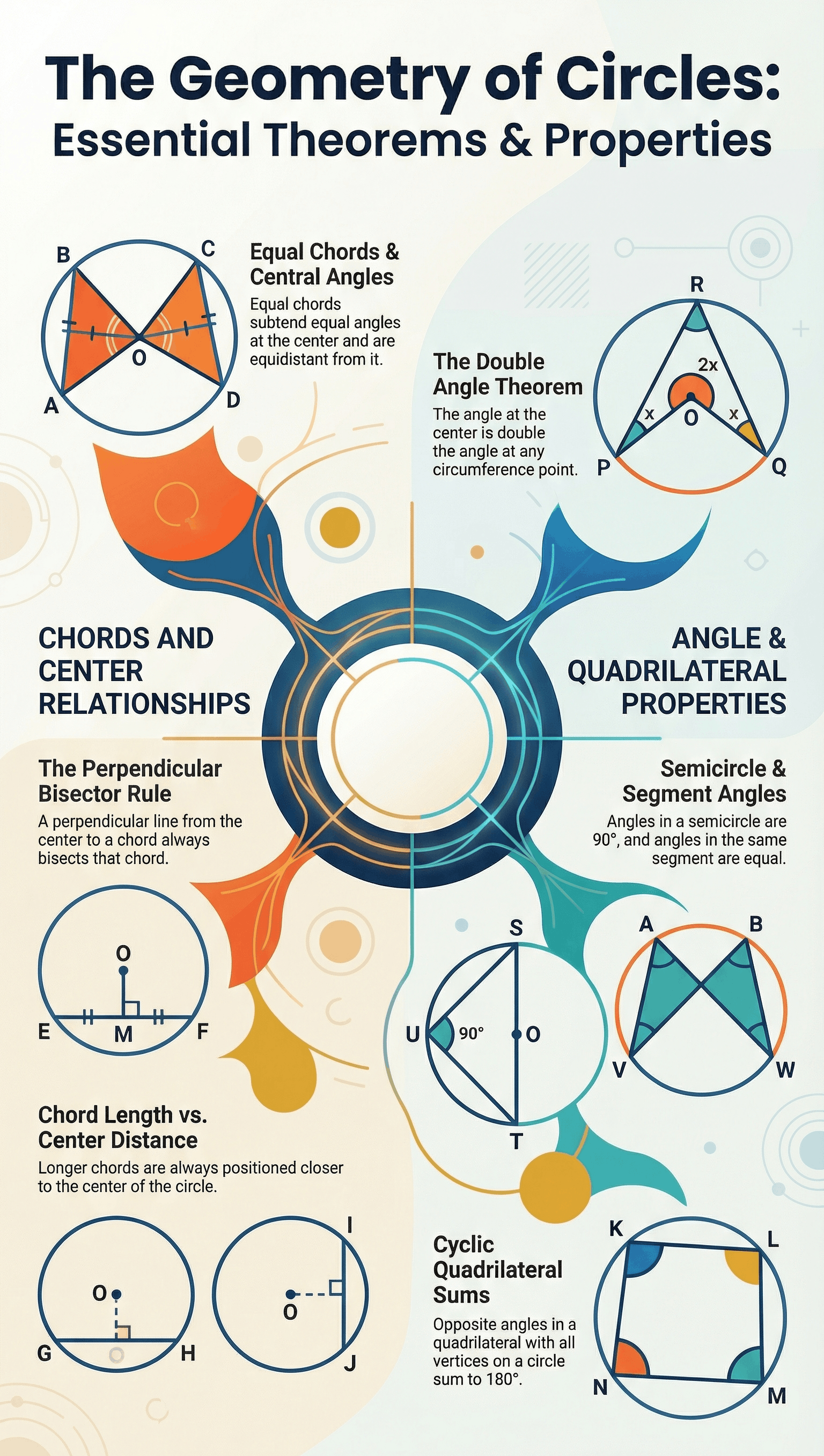
- Equal Chords: Equal chords of a circle (or congruent circles) subtend equal angles at the centre.
- Converse: If the angles subtended by two chords at the centre are equal, then the chords themselves are equal in length.
- Perpendicular Bisector: A perpendicular drawn from the centre of a circle to a chord always bisects that chord.
- Inverse Property: A line drawn through the centre of a circle to bisect a chord is necessarily perpendicular to that chord.
Distances from the Centre
- Equidistance: Equal chords of a circle are at an equal distance (equidistant) from the centre.
- Distance Property: Chords that are equidistant from the centre of a circle are equal in length.
- Chord Length vs. Distance: Longer chords are nearer to the centre than smaller chords. The diameter, being the longest chord, has a distance of zero from the centre.
Arcs and Angles
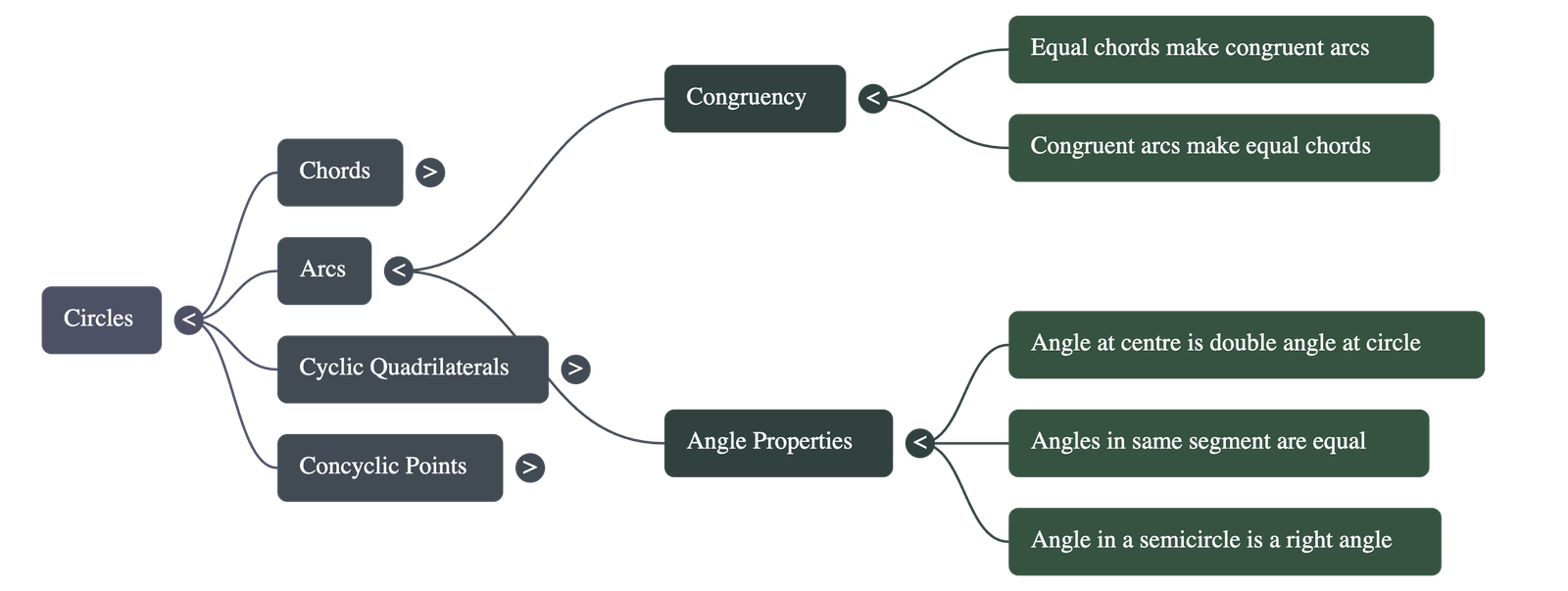
- Congruent Arcs: If two chords of a circle are equal, their corresponding arcs are congruent. Conversely, if two arcs are congruent, their corresponding chords are equal.
- The Degree Measure Theorem: The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
- Same Segment: Angles formed in the same segment of a circle are always equal to each other.
- Semicircle Property: Any angle formed within a semicircle is a right angle (90°).
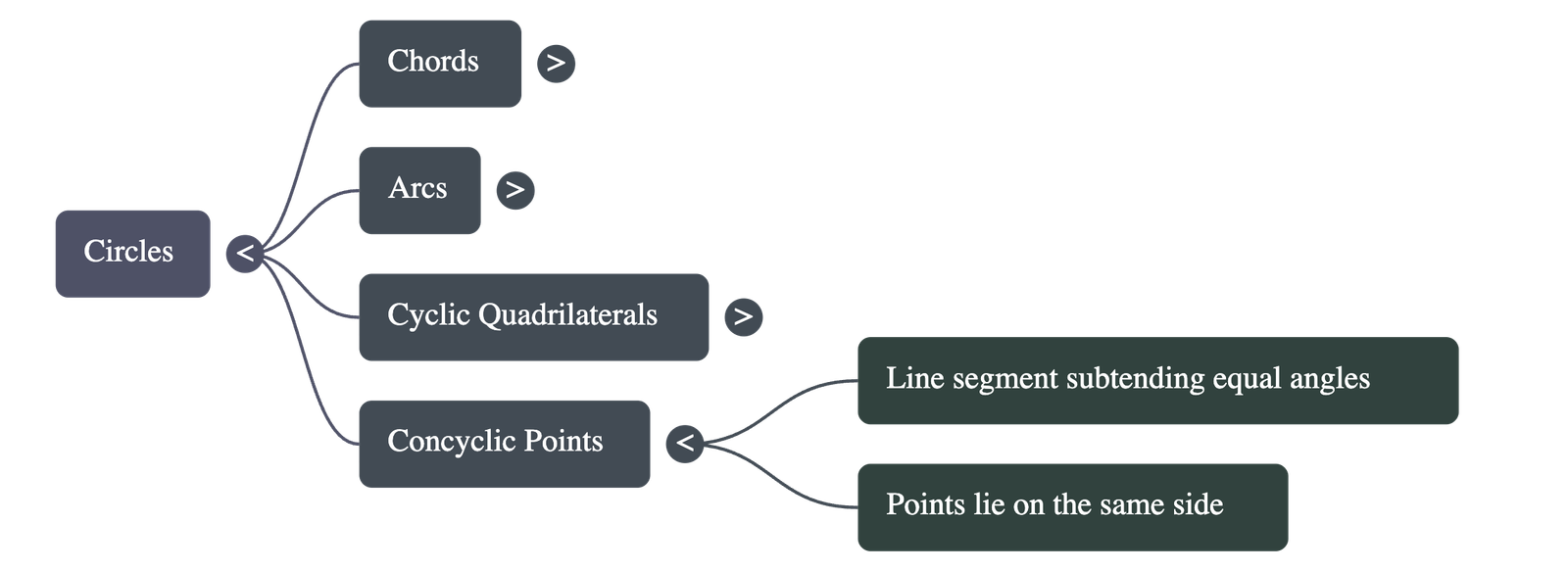
- Concyclic Points: If a line segment joining two points subtends equal angles at two other points on the same side of the line, then all four points lie on the same circle.
Cyclic Quadrilaterals
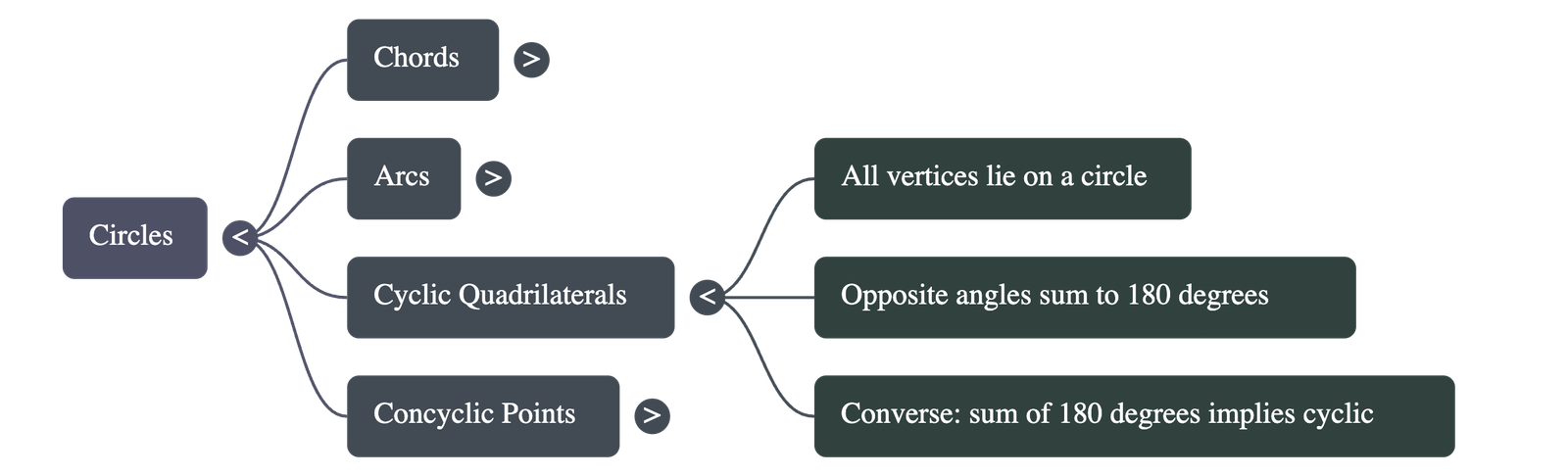
- Definition: A quadrilateral is called cyclic if all four of its vertices lie on the circumference of a circle.
- Opposite Angles: The sum of either pair of opposite angles in a cyclic quadrilateral is always 180°.
- Verification: If the sum of a pair of opposite angles of a quadrilateral is 180°, then the quadrilateral is guaranteed to be cyclic.
Quick Navigation:
| | |
1 / 1
Quick Navigation:
| | |