QUADRILATERALS

Basic Concepts

• A quadrilateral is a polygon with four sides, four angles, and four vertices.
• A parallelogram is a specific type of quadrilateral where both pairs of opposite sides are parallel.

Properties of a Parallelogram

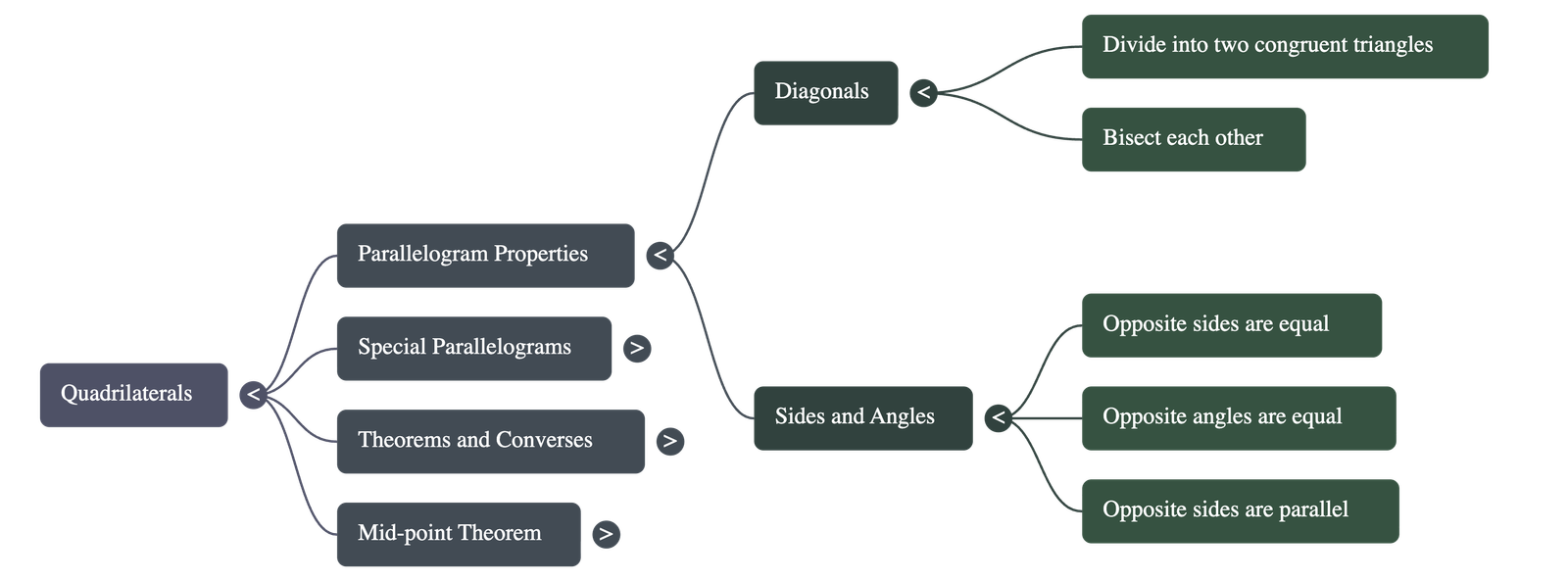
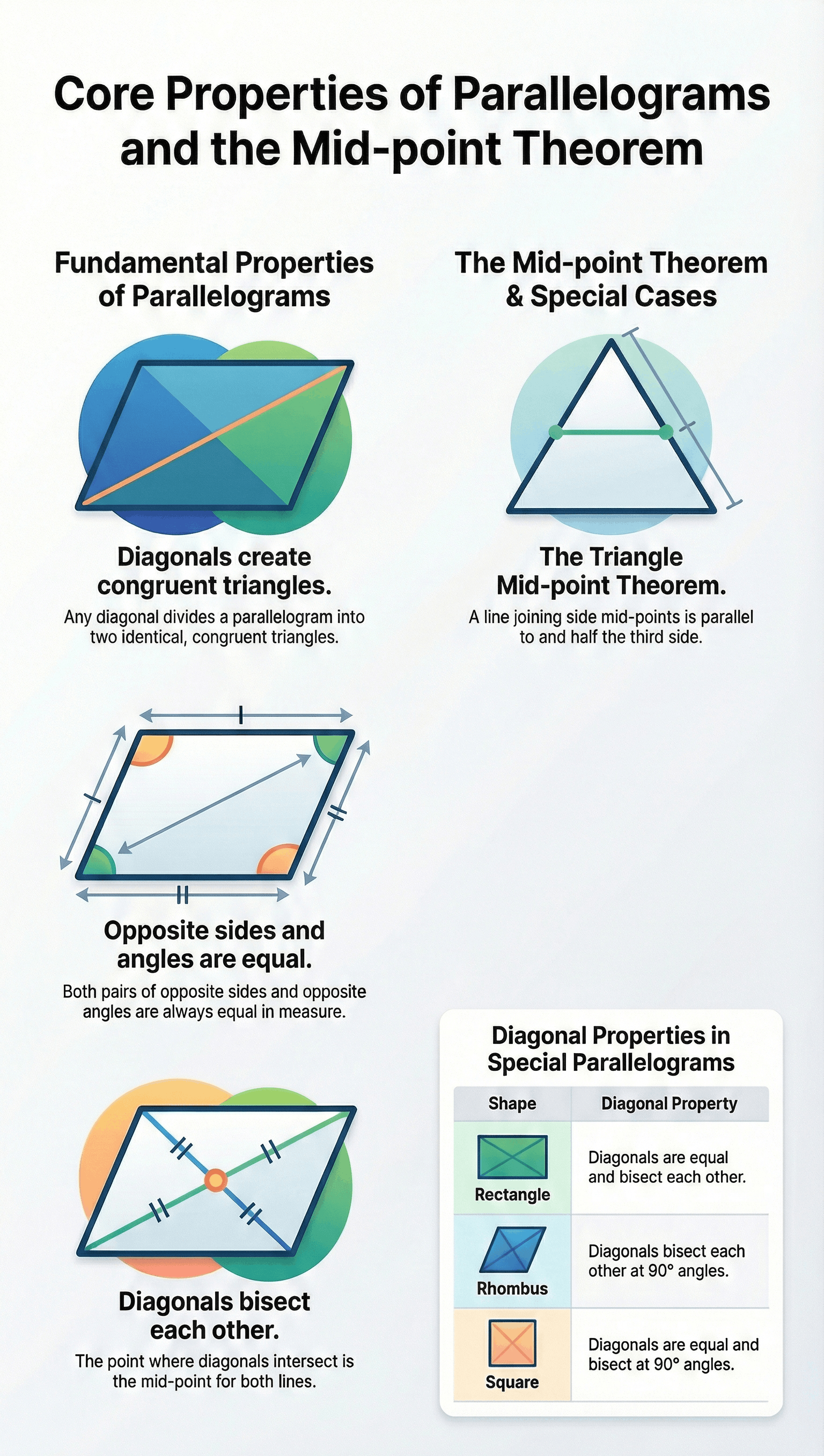
• Congruent Triangles: A diagonal of a parallelogram divides the shape into two congruent triangles.
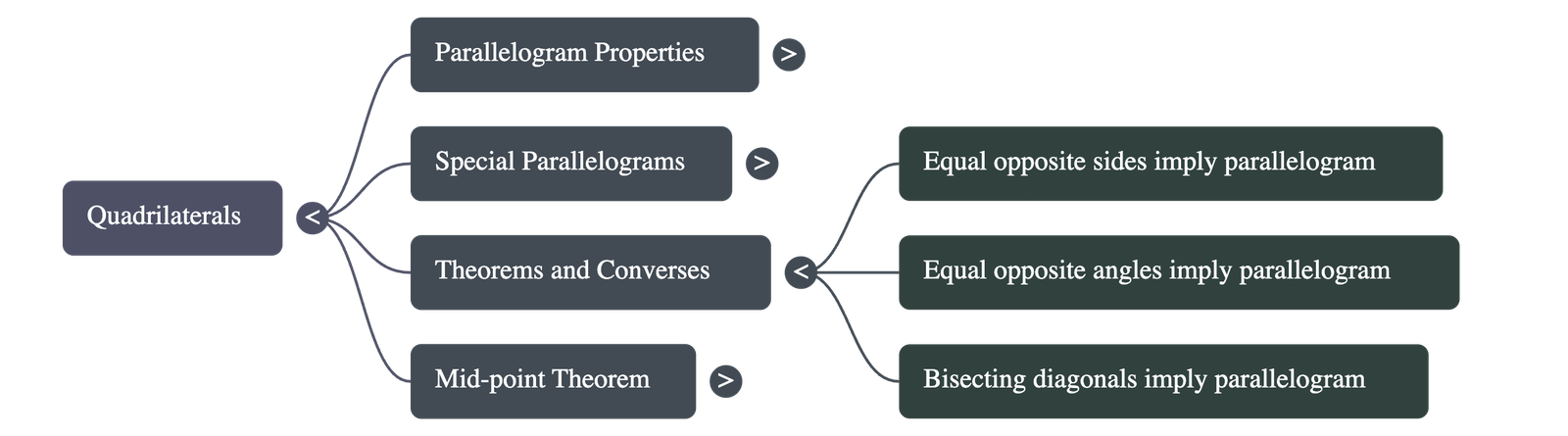
• Opposite Sides: In any parallelogram, the opposite sides are equal in length. Conversely, if each pair of opposite sides of a quadrilateral is equal, it is a parallelogram.
• Opposite Angles: The opposite angles in a parallelogram are equal. Conversely, if each pair of opposite angles in a quadrilateral is equal, it is a parallelogram.
• Diagonal Bisectors: The diagonals of a parallelogram bisect each other. Conversely, if the diagonals of a quadrilateral bisect each other, the shape is a parallelogram.

Special Quadrilaterals

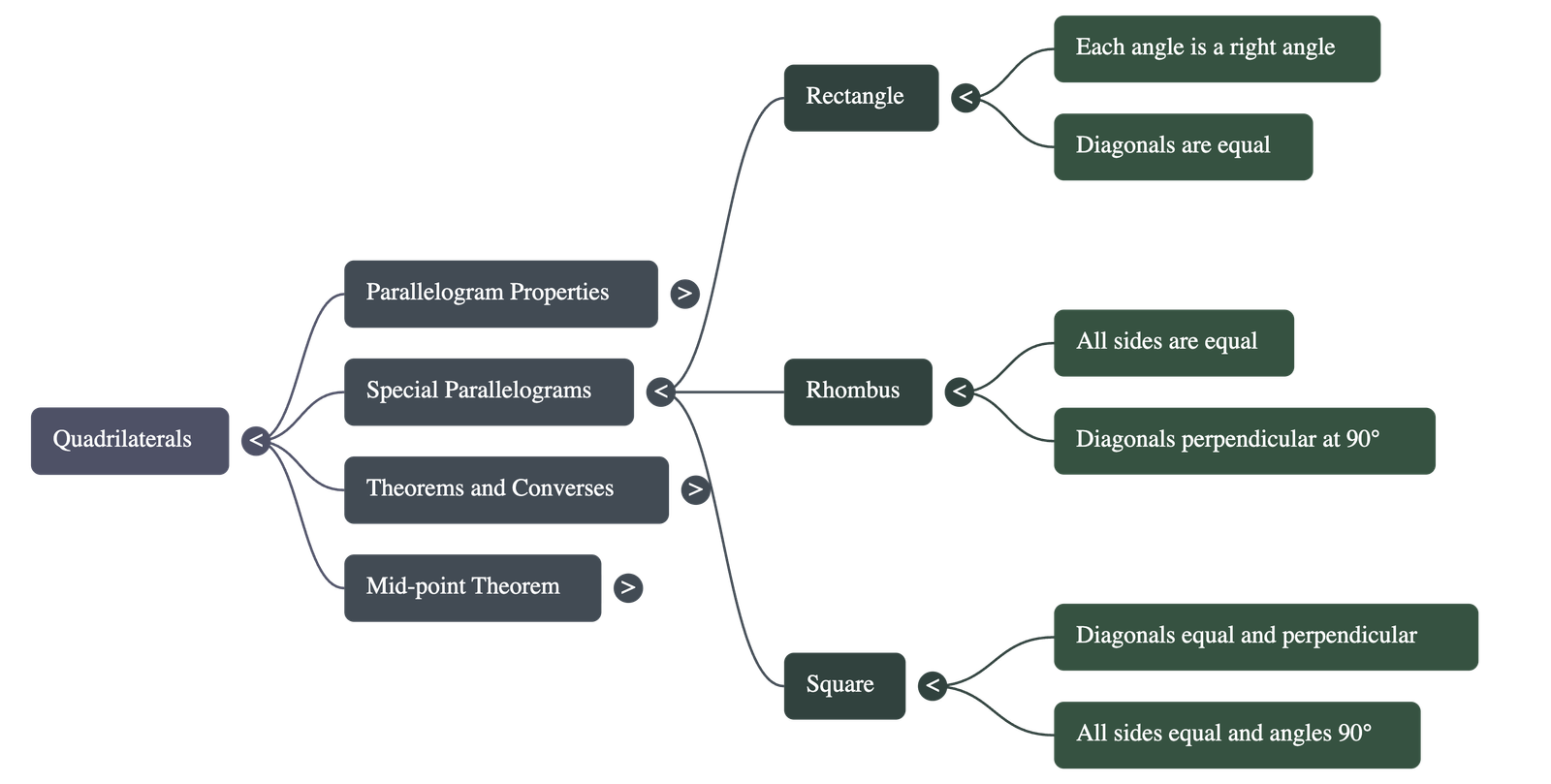
• Rectangle: A rectangle is a parallelogram where one angle is a right angle. Consequently, all angles in a rectangle are right angles. Its diagonals bisect each other and are equal in length.
• Rhombus: A rhombus is a quadrilateral with all sides of equal length. Its diagonals are perpendicular to each other and bisect each other at right angles.
• Square: A square is a parallelogram with all sides equal and all angles equal to 90 degrees. Its diagonals are equal and bisect each other at right angles.

The Mid-point Theorem

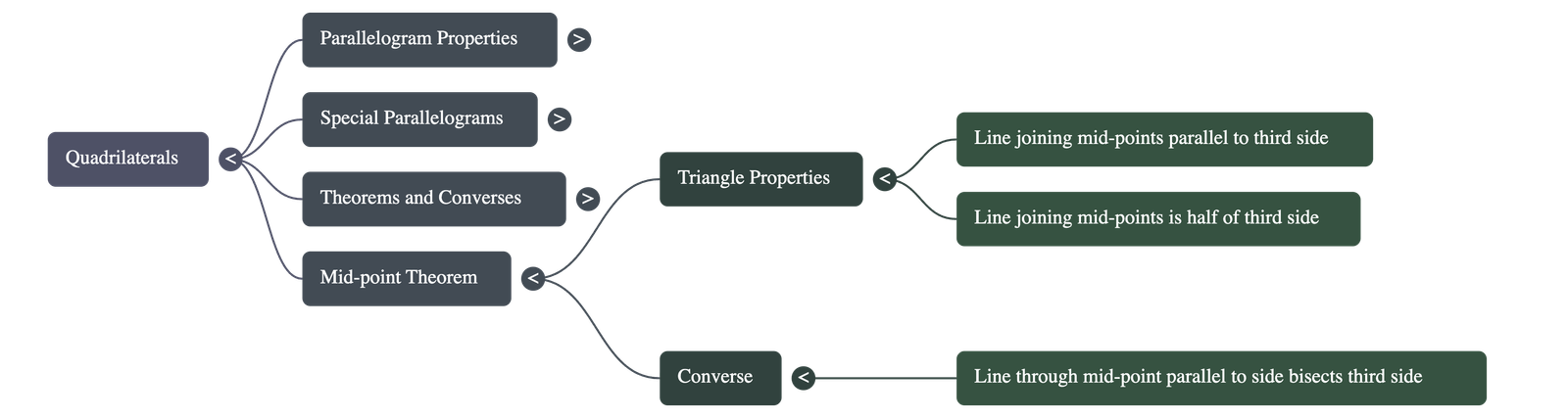
• Theorem: The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.
• Converse: A line drawn through the mid-point of one side of a triangle, parallel to another side, will bisect the third side.

Key Summary Points