LINES AND ANGLES

1. Introduction and Practical Applications

• The study of lines and angles is fundamental to geometry and is used to prove statements using deductive reasoning.
• Knowledge of these properties is essential in daily life and professional fields, such as architecture for building layouts, science for drawing light ray diagrams (refraction), and engineering to study the effect of forces acting on a body.

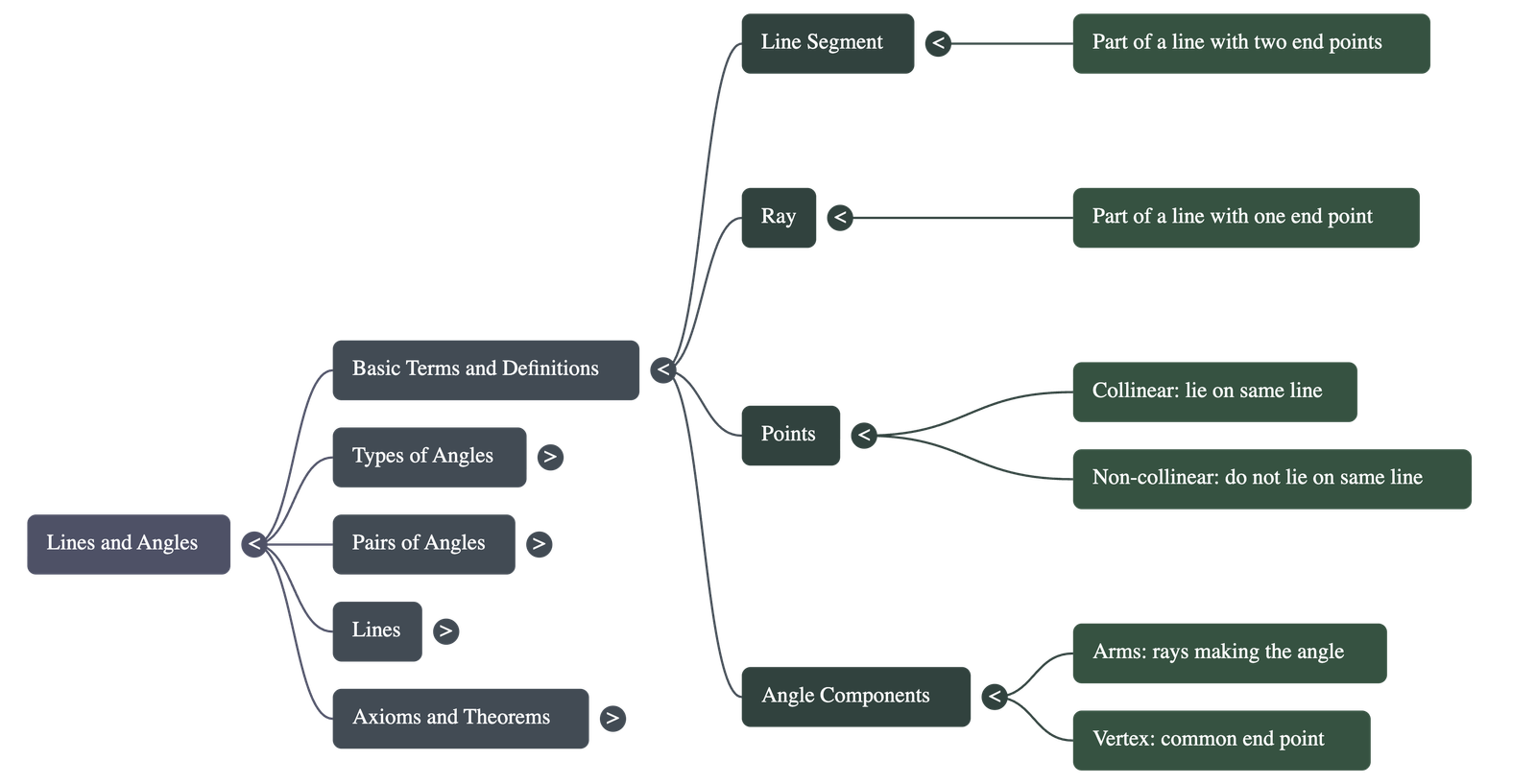
2. Basic Terms and Definitions

• Line Segment: A part of a line that has two end points.
• Ray: A part of a line with only one end point.
• Collinear Points: Three or more points that lie on the same straight line; otherwise, they are called non-collinear points.
• Angle Formation: An angle is created when two rays (called arms) originate from the same end point (called the vertex).

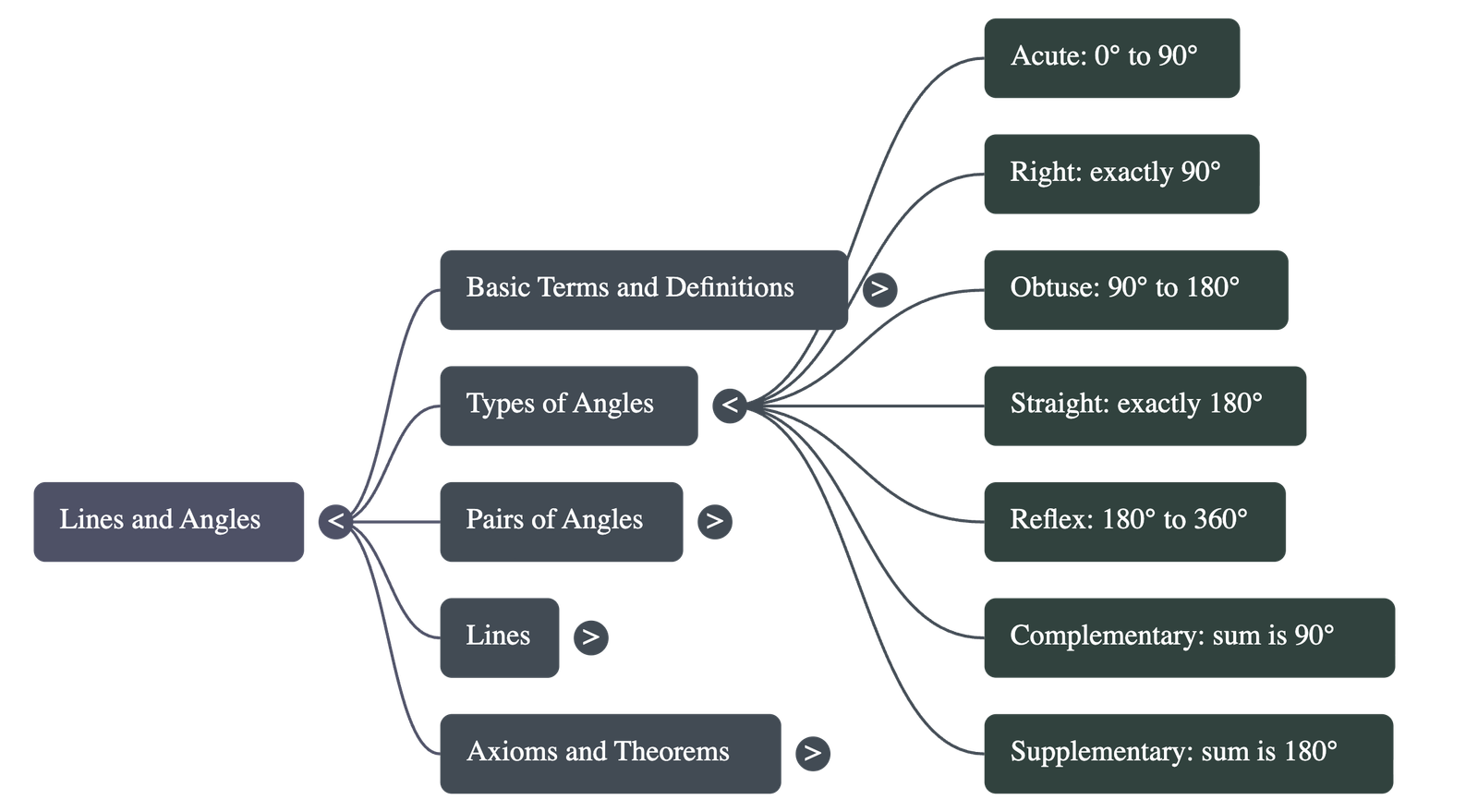
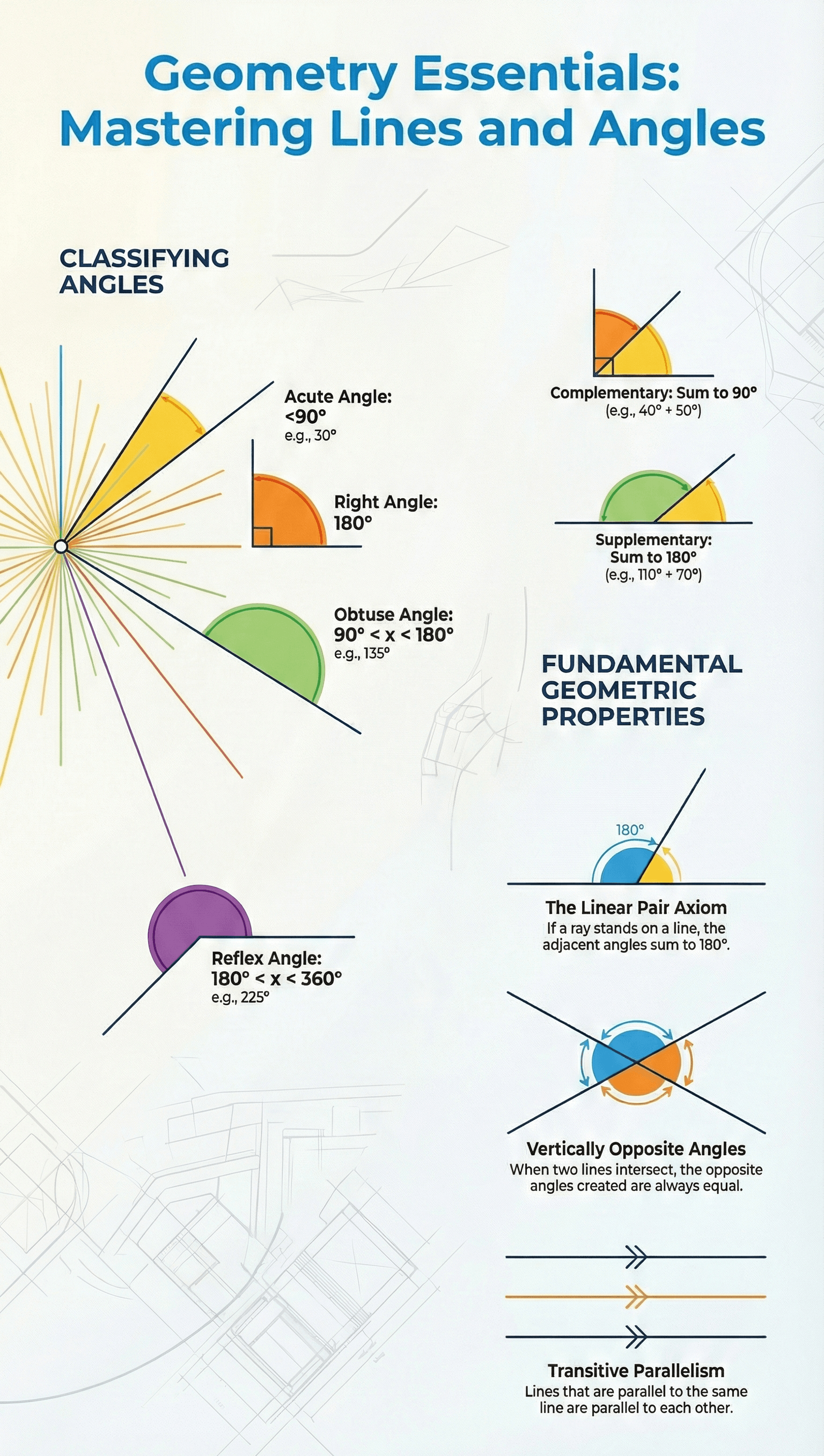
3. Types of Angles

• Acute Angle: Measures between 0° and 90°.
• Right Angle: Exactly equal to 90°.
• Obtuse Angle: Greater than 90° but less than 180°.
• Straight Angle: Exactly equal to 180°.
• Reflex Angle: Greater than 180° but less than 360°.
• Complementary Angles: Two angles whose sum is 90°.
• Supplementary Angles: Two angles whose sum is 180°.

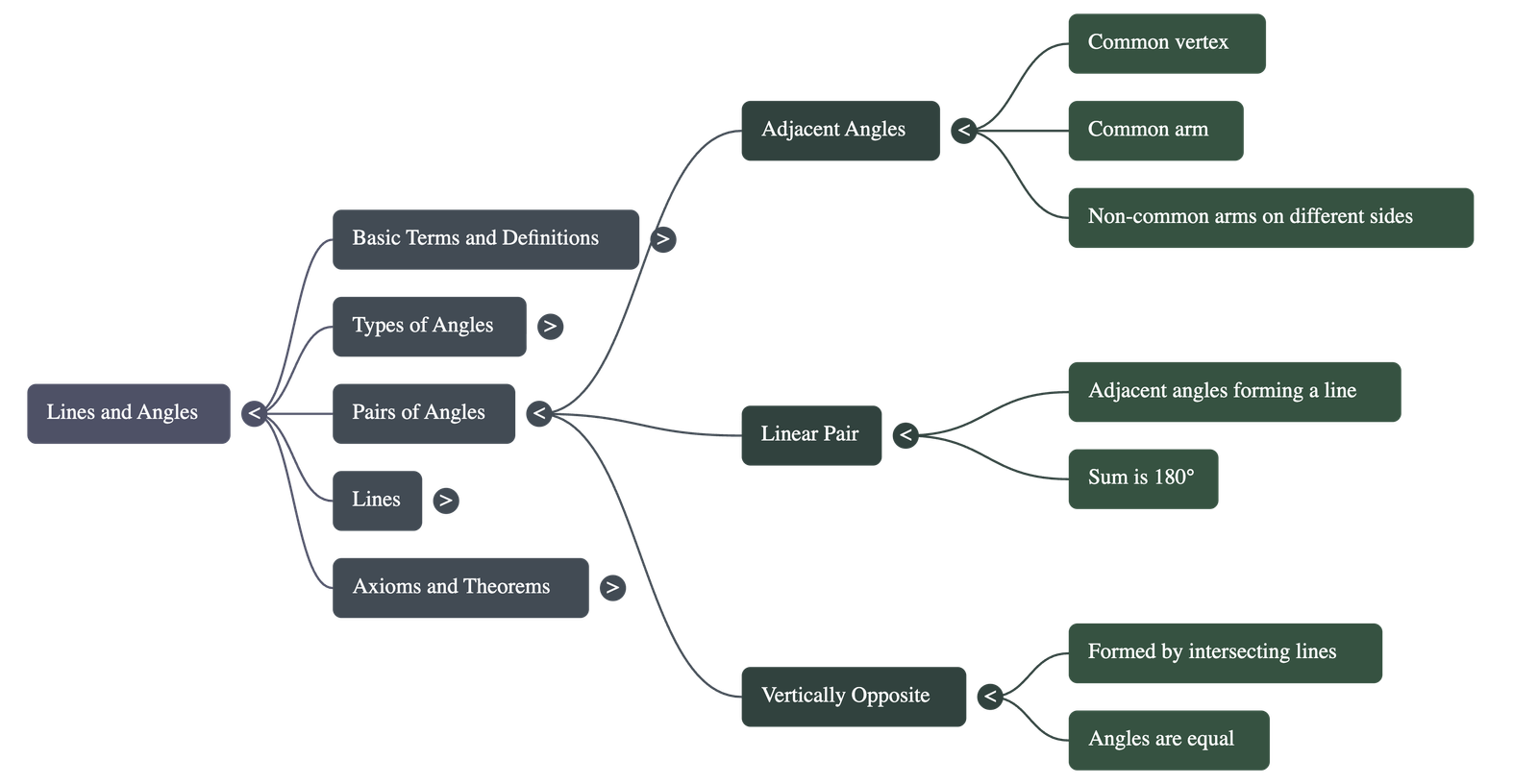
4. Angle Relations and Pairs

• Adjacent Angles: Two angles that share a common vertex, a common arm, and have their non-common arms on opposite sides of the common arm. The sum of adjacent angles equals the angle formed by the non-common arms.
• Linear Pair of Angles: Formed when the non-common arms of two adjacent angles form a straight line.
• Vertically Opposite Angles: Formed when two lines intersect at a point. There are two pairs of such angles, and they are always equal.

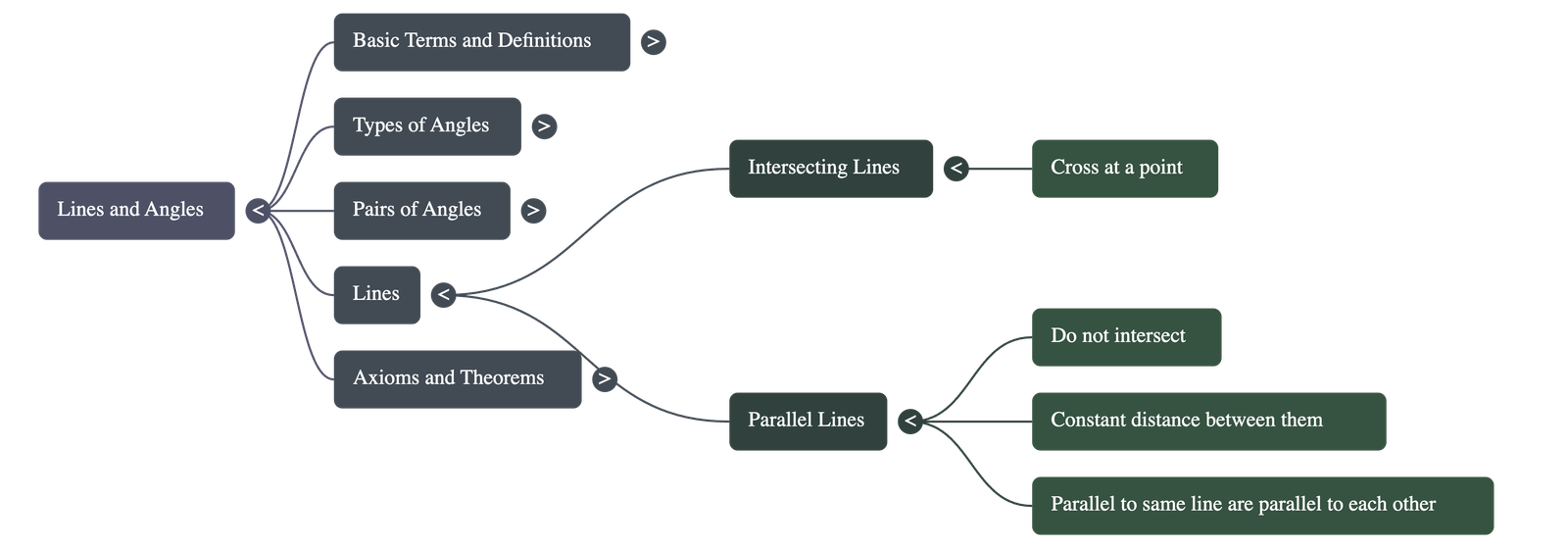
5. Intersecting and Parallel Lines

• Intersecting Lines: Lines that cross each other at a single point.
• Parallel (Non-intersecting) Lines: Lines that never meet, even when extended indefinitely. The distance between them, measured by a common perpendicular, is constant at all points.

6. Key Axioms and Theorems

• Linear Pair Axiom: If a ray stands on a line, the sum of the two adjacent angles is 180°. Conversely, if the sum of two adjacent angles is 180°, the non-common arms form a line.
• Theorem on Intersecting Lines: If two lines intersect each other, then the vertically opposite angles are equal.
• Lines Parallel to the Same Line: Lines which are parallel to the same line are parallel to each other. This property can be extended to more than two lines.