Quick Navigation:
| | |
TRIANGLES
1. Introduction to Triangles
- Definition: A triangle is a closed figure formed by three intersecting lines.
- Components: Every triangle consists of three sides, three angles, and three vertices.
- Notation: A triangle with vertices A, B, and C is denoted as Δ ABC.
2. Understanding Congruence
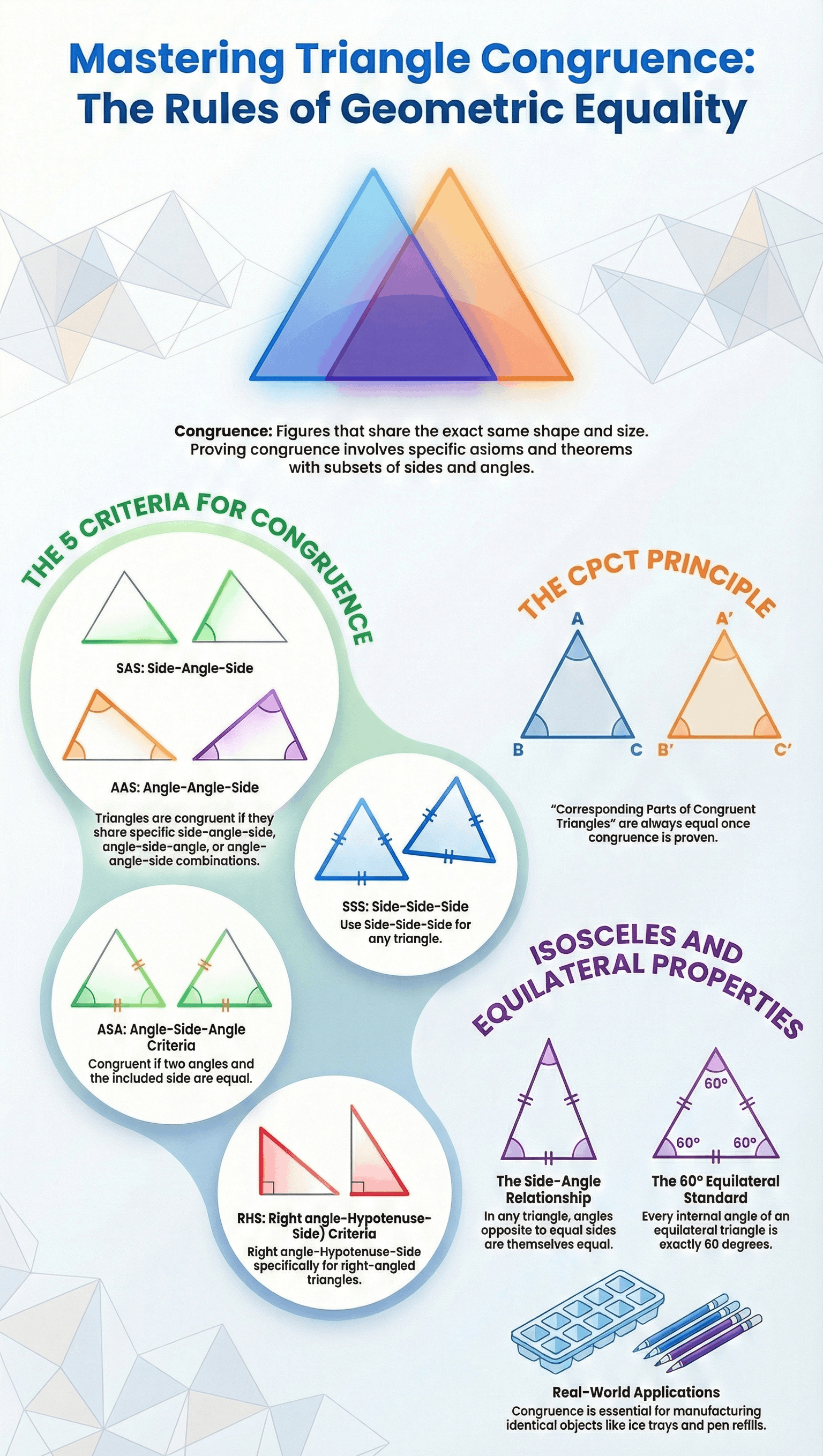
- Concept: Congruent figures are equal in all respects, meaning they have the exact same shape and size.
- Congruent Triangles: Two triangles are congruent if the sides and angles of one are equal to the corresponding sides and angles of the other.
- CPCT: This stands for "Corresponding Parts of Congruent Triangles." When two triangles are proven congruent, their remaining corresponding parts are automatically equal.
- Symbolic Form: Congruence is written using the symbol ≅ (e.g., Δ ABC ≅ Δ PQR). It is essential to write the vertices in the correct corresponding order.
3. Criteria for Congruence of Triangles
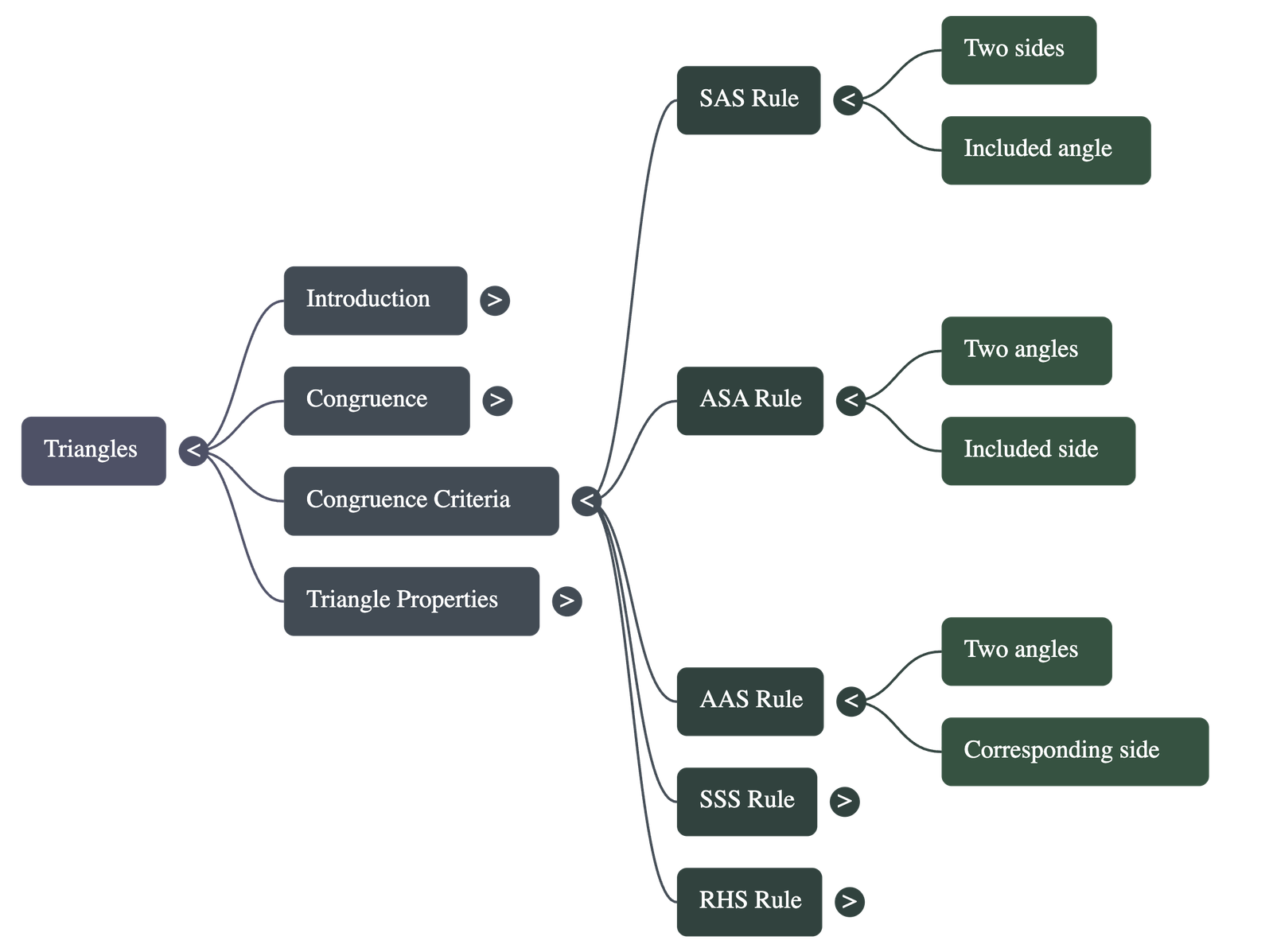
The sources outline five main rules to determine if two triangles are congruent:
SAS (Side-Angle-Side): Two triangles are congruent if two sides and the included angle of one are equal to two sides and the included angle of the other.
ASA (Angle-Side-Angle): Two triangles are congruent if two angles and the included side of one are equal to two angles and the included side of the other.
AAS (Angle-Angle-Side): Two triangles are congruent if two angles and one corresponding side are equal. This is valid even if the side is not included between the angles.
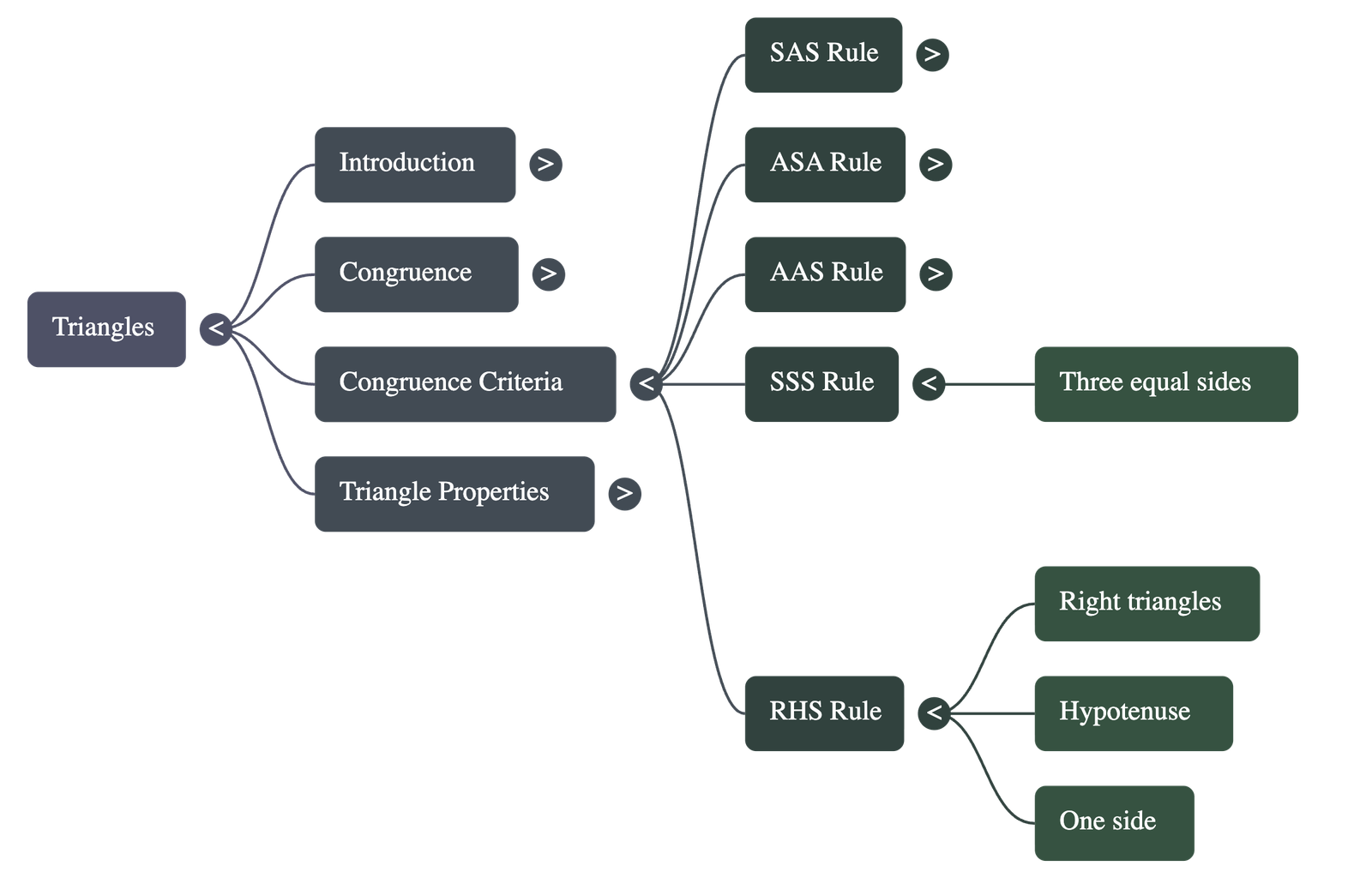
SSS (Side-Side-Side): If all three sides of one triangle are equal to the three sides of another triangle, the triangles are congruent.
RHS (Right angle-Hypotenuse-Side): In two right-angled triangles, if the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other, they are congruent.
4. Properties of Isosceles and Equilateral Triangles
- Equal Angles: In an isosceles triangle (a triangle with two equal sides), the angles opposite to the equal sides are also equal.
- Equal Sides (Converse): Conversely, the sides opposite to equal angles of a triangle are equal.
- Equilateral Triangles: In an equilateral triangle, all three sides are equal, and each internal angle measures exactly 60°.
Key Summary Points
In summary, congruence requires more than just equal angles; at least one side must be equal for two triangles to be identical. The study of triangle properties and congruence criteria allows for solving complex geometric problems by identifying corresponding equal parts and using logic to prove relationships between different line segments and angles.
Quick Navigation:
| | |
1 / 1
Quick Navigation:
| | |