Chapter 1: Number Systems
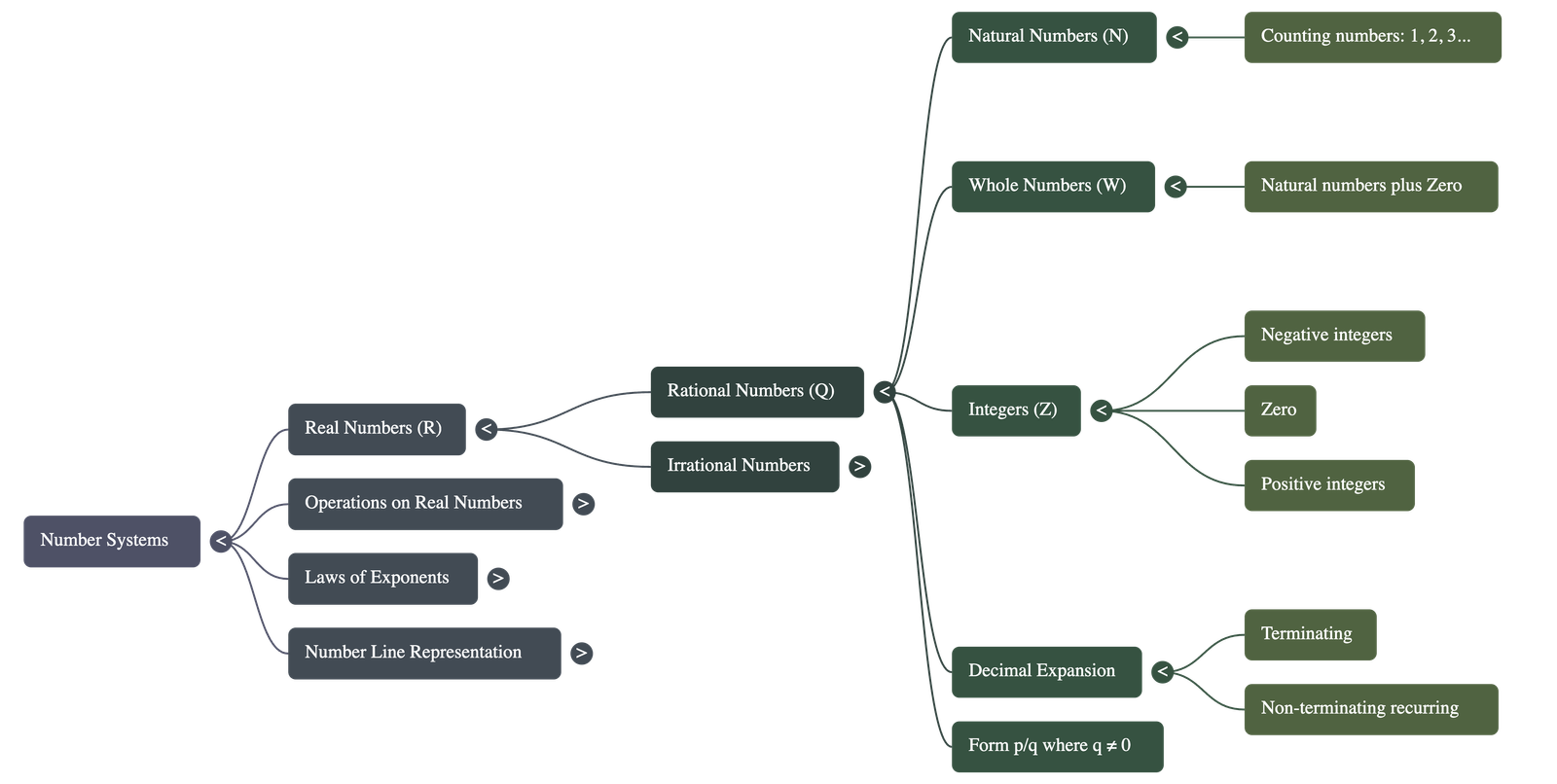
1. Classification of Numbers
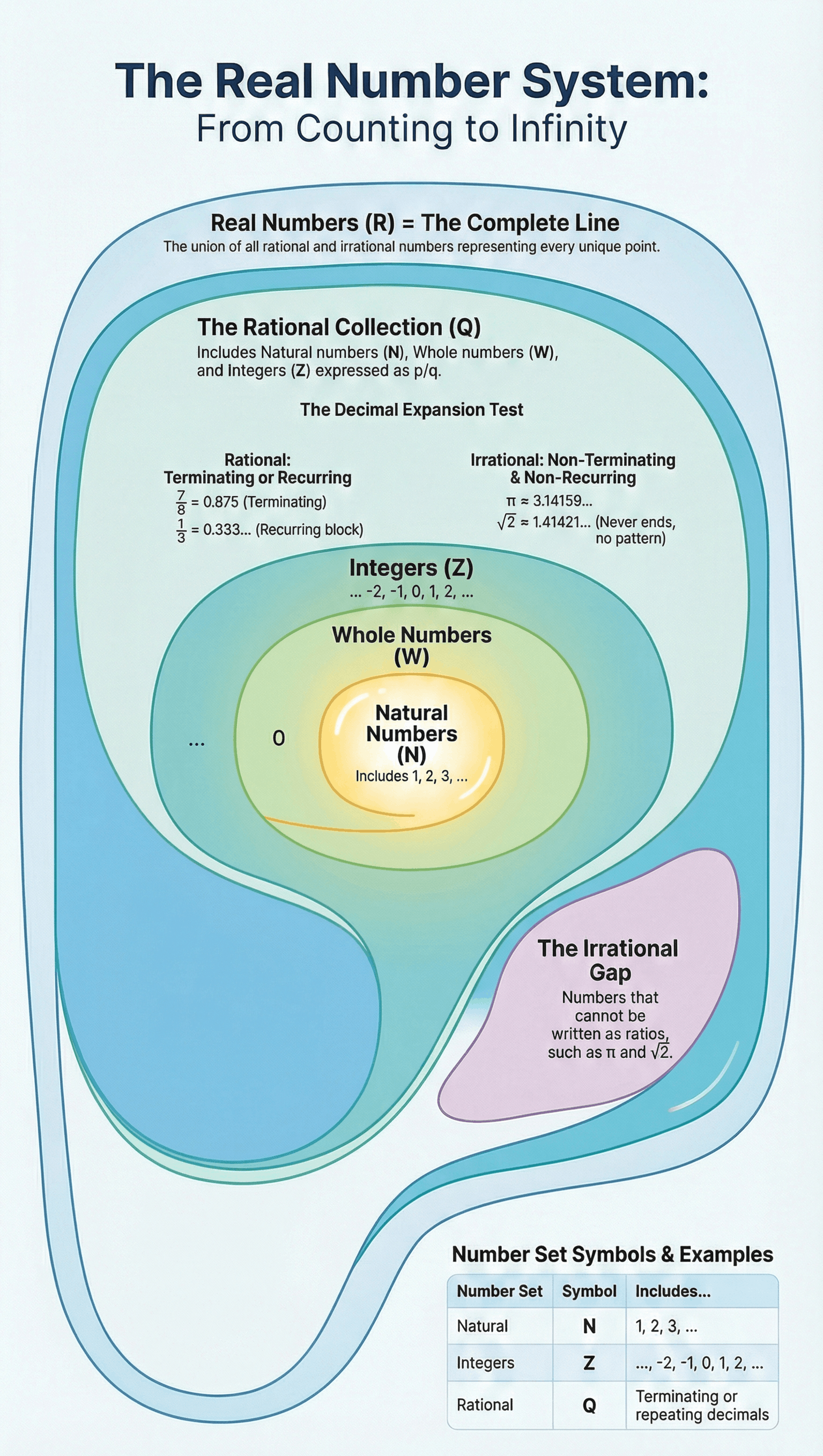
- Natural Numbers (N): The counting numbers starting from 1 (1, 2, 3, ...).
- Whole Numbers (W): The collection of natural numbers including zero (0, 1, 2, 3, ...).
- Integers (Z): The collection of all whole numbers and the negative of natural numbers (..., -3, -2, -1, 0, 1, 2, 3, ...). The symbol 'Z' comes from the German word zahlen (to count).
- Rational Numbers (Q): A number 'r' is rational if it can be written in the form p/q, where 'p' and 'q' are integers and q ≠ 0.
- The rational numbers include natural numbers, whole numbers, and integers.
- There are infinitely many rational numbers between any two given rational numbers.
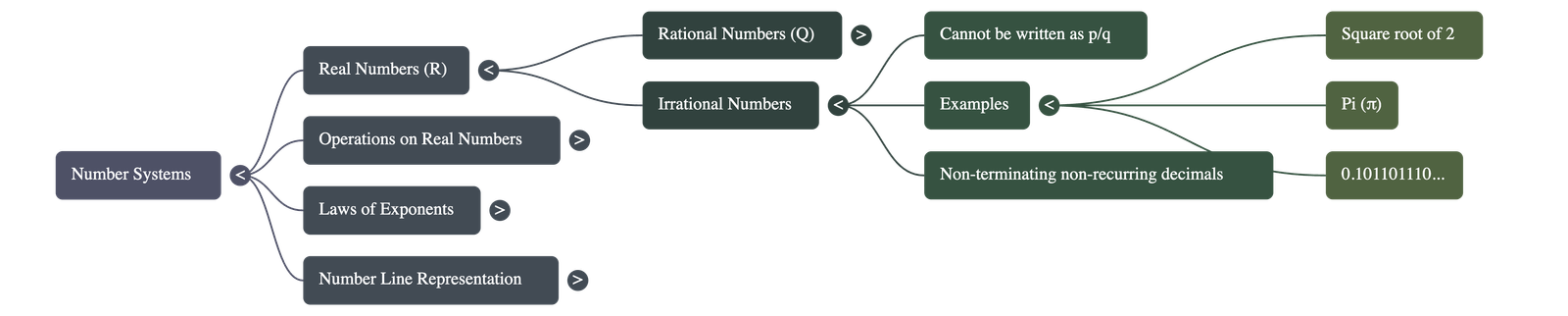
2. Irrational Numbers
A number 's' is called irrational if it cannot be written in the form p/q, where p and q are integers and q ≠ 0.
- Discovery: Discovered by the Pythagoreans in Greece (around 400 BC).
- Examples: √2, √3, √5, √15, π, and numbers like 0.101101110...
- Square Roots: The square roots of positive integers which are not perfect squares are irrational (e.g., √2 is irrational, but √4 is rational because it equals 2).
3. Real Numbers and the Number Line
The collection of all rational numbers and irrational numbers together forms the collection of Real Numbers (R).
- Every real number is represented by a unique point on the number line.
- Conversely, every point on the number line represents a unique real number. Therefore, the number line is often called the real number line.
- Irrational numbers like √n (where n is a positive integer) can be located geometrically on the number line using the Pythagoras theorem.
4. Decimal Expansions
Real numbers can be distinguished by the nature of their decimal expansions:
Rational Numbers
The decimal expansion of a rational number is either:
- Terminating: The remainder becomes zero after some steps (e.g., 7/8 = 0.875).
- Non-terminating Recurring (Repeating): The remainder never becomes zero, and a block of digits repeats periodically (e.g., 10/3 = 3.333...).
Irrational Numbers
The decimal expansion of an irrational number is Non-terminating Non-recurring. (e.g., π = 3.141592... with no repeating pattern).
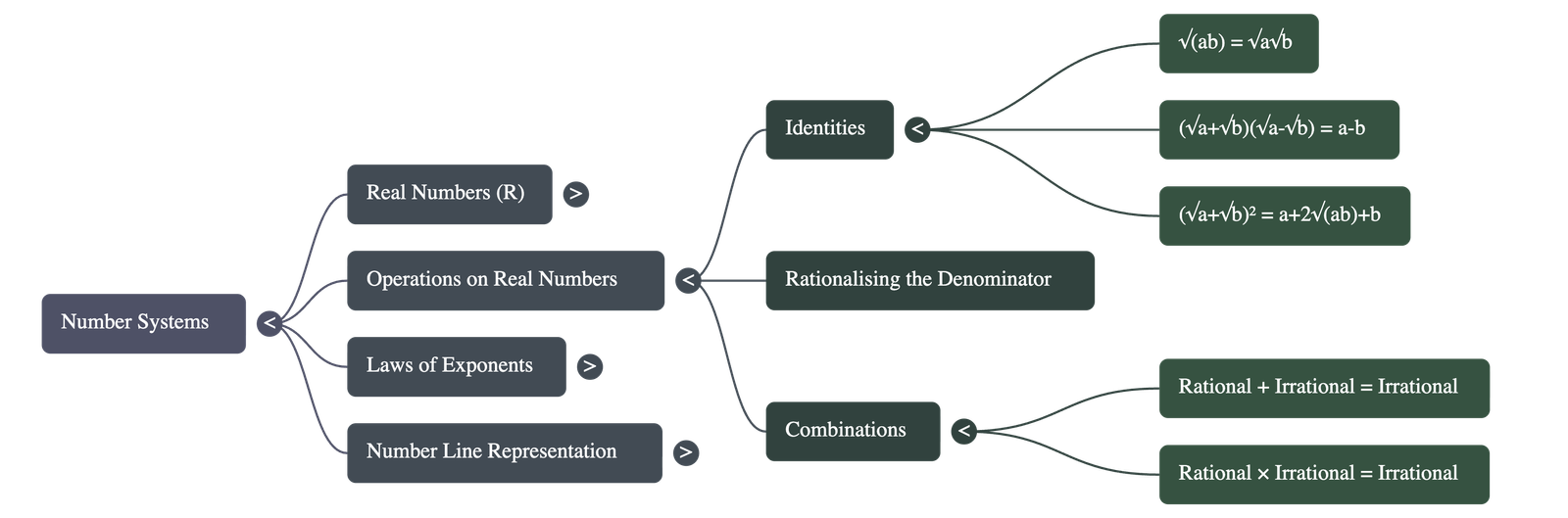
5. Operations on Real Numbers
Rational and irrational numbers satisfy the commutative, associative, and distributive laws, but specific rules apply to their combinations:
- Addition/Subtraction: The sum or difference of a rational number and an irrational number is irrational.
- Multiplication/Division: The product or quotient of a non-zero rational number with an irrational number is irrational.
- Two Irrationals: If you add, subtract, multiply, or divide two irrational numbers, the result may be rational or irrational.
6. Identities Involving Square Roots
For positive real numbers a and b:
- √(ab) = √a × √b
- √(a/b) = √a / √b
- (√a + √b)(√a - √b) = a - b
- (a + √b)(a - √b) = a² - b
- (√a + √b)² = a + 2√(ab) + b
7. Rationalising the Denominator
When the denominator of an expression contains a square root, the process of converting it into an equivalent expression with a rational denominator is called rationalising the denominator.
Method: Use the identity (x + y)(x - y) = x² - y².
Example: To rationalise 1 / (√a + b), multiply the numerator and denominator by the conjugate (√a - b).
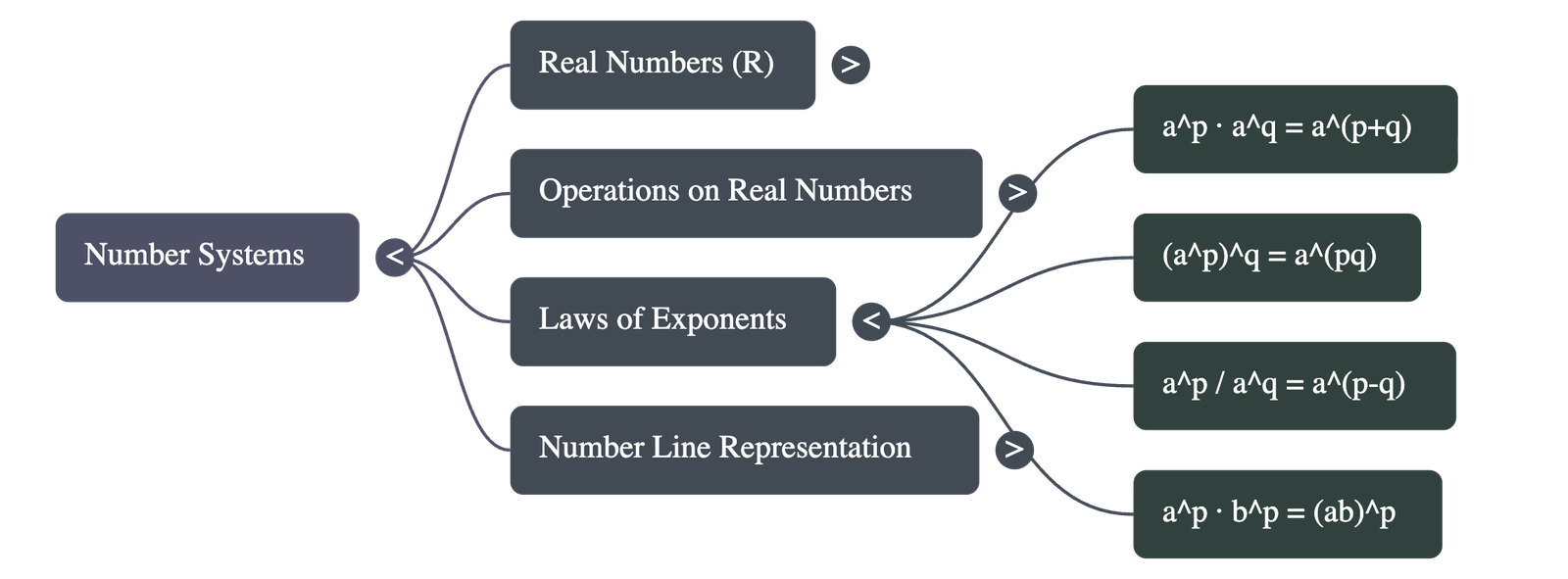
8. Laws of Exponents for Real Numbers
Let a > 0 be a real number and p and q be rational numbers. The following laws hold:
- Multiplication: ap · aq = ap + q
- Power of a Power: (ap)q = apq
- Division: ap / aq = ap - q
- Different Bases: apbp = (ab)p
- Negative Exponents: a-n = 1 / an
- Fractional Exponents: am/n = n√(am)
- Zero Exponent: a0 = 1