Chapter 10: Work and Energy

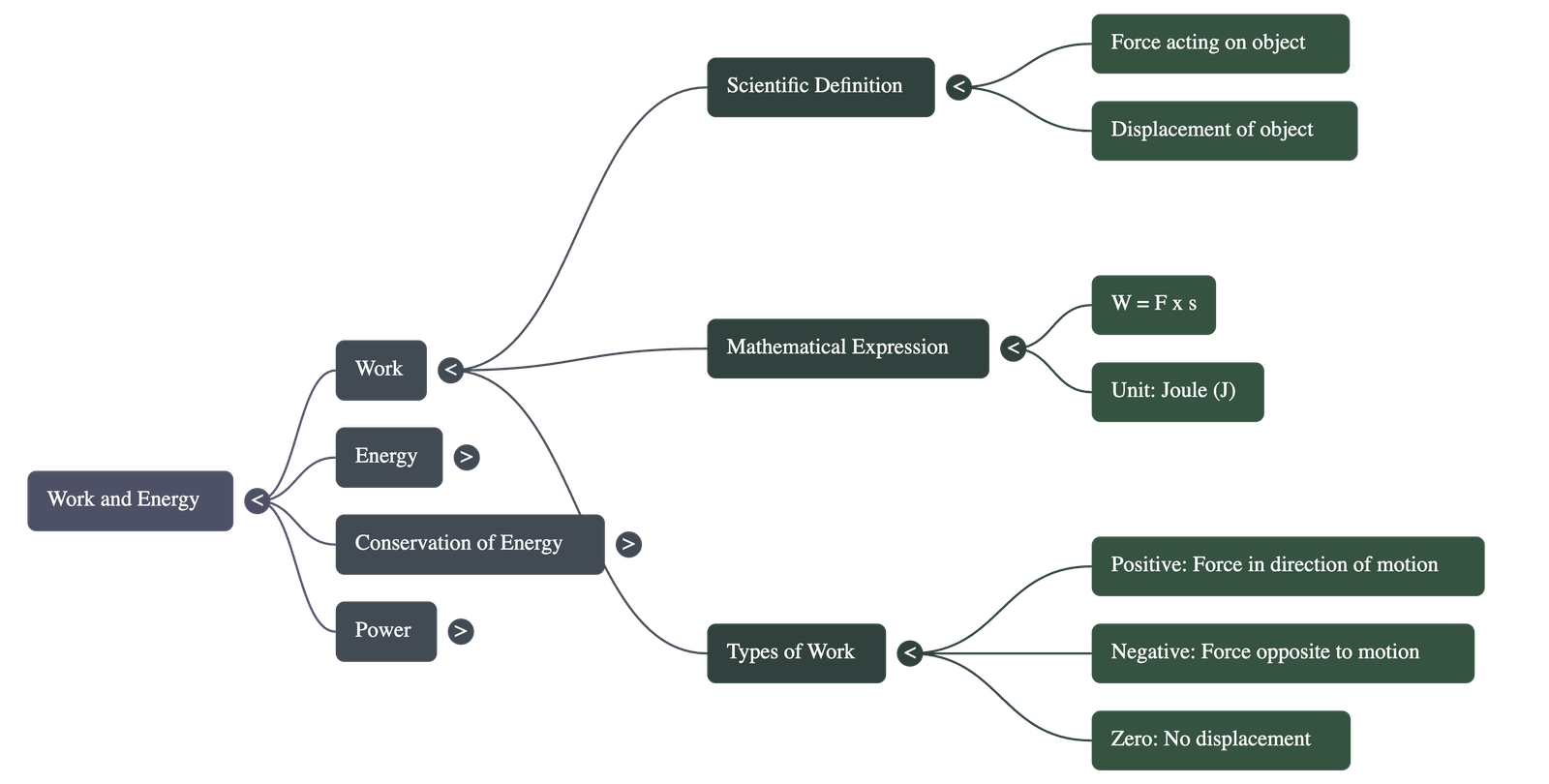
10.1 Work

The Scientific Conception of Work

• Difference from Daily Life: Common activities like reading, thinking hard, holding a heavy load on one's head without moving, or pushing a rock that doesn't move are considered "hard work" in everyday language but constitute no work in science.
• Two Conditions for Work:
  1. A force must act on an object.
  2. The object must be displaced.
• If either condition is not met (e.g., displacement is zero), no work is done.

Work Done by a Constant Force

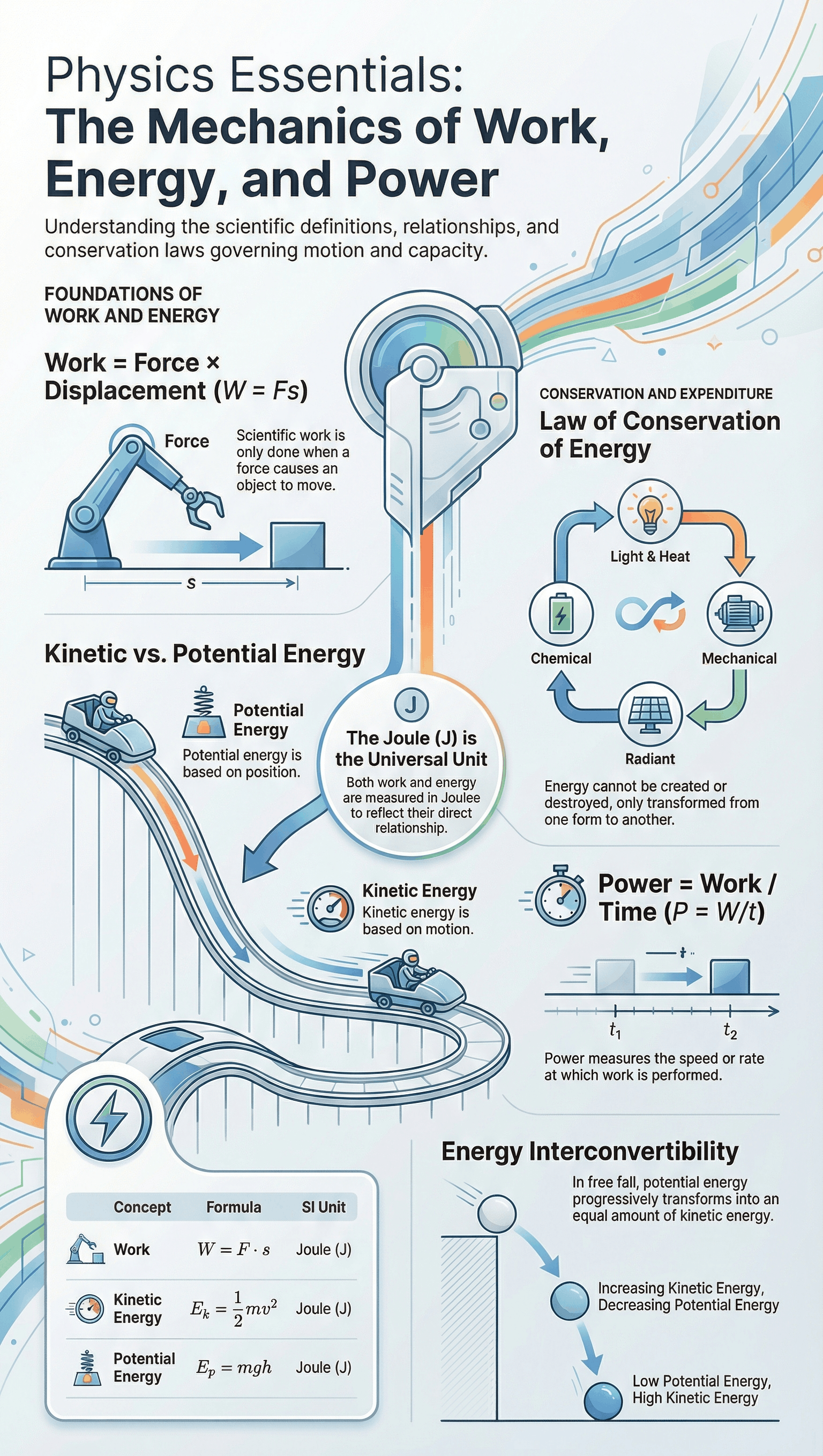
• Definition: Work done is the product of the force and the displacement in the direction of the force.
• Formula: W = F × s (where F is Force and s is displacement).
• Quantity: Work is a scalar quantity; it has only magnitude and no direction.
• Unit: The SI unit is the Joule (J) or newton metre (N m).
  Definition of 1 Joule: The amount of work done on an object when a force of 1 N displaces it by 1 m along the line of action of the force.

Positive and Negative Work

• Positive Work: Work is positive when the force acts in the direction of displacement (e.g., a baby pulling a toy car, lifting an object up).
• Negative Work: Work is negative when the force acts opposite to the direction of displacement (e.g., friction acting against a moving object, or gravity acting on an object being lifted). The formula becomes W = F × (-s).

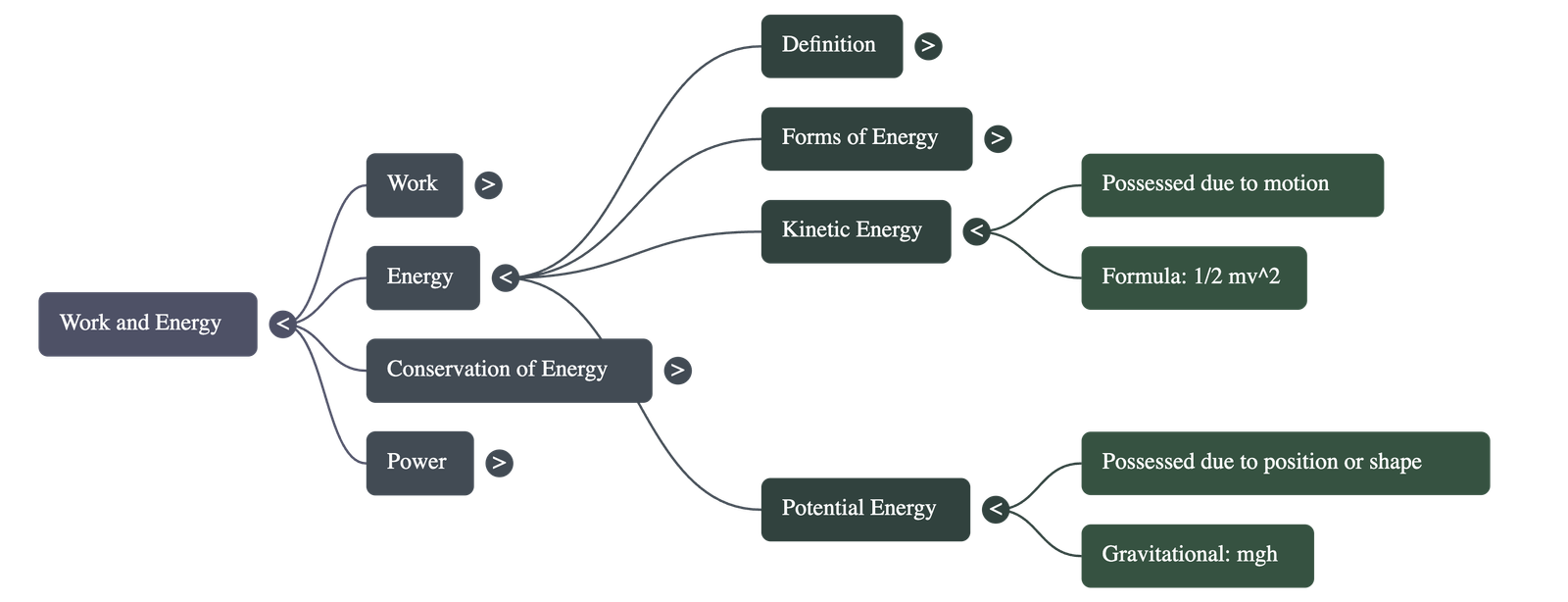
10.2 Energy

• Definition: Energy is the capability to do work. An object possessing energy can exert a force on another object to transfer energy.
• Transfer: The object doing the work loses energy, and the object on which work is done gains energy.
• Unit: Same as work: Joule (J). Larger unit: kilojoule (kJ), where 1 kJ = 1000 J.
• Forms of Energy: Mechanical energy (Kinetic + Potential), heat, chemical, electrical, and light energy. The Sun is the ultimate source for many energy forms.

Kinetic Energy

• Definition: The energy possessed by an object due to its motion. Moving objects like a bullet, blowing wind, or a running athlete possess kinetic energy.
• Factors: Kinetic energy increases with the speed of the object. A faster-moving object can do more work than a slower one of the same mass.
• Formula: For an object of mass m moving with uniform velocity v:
  
  E_k = ½ m v²
• Relation to Work: The work done on an object to change its velocity is equal to the change in its kinetic energy.

Potential Energy

• Definition: The energy present in an object by virtue of its position or configuration (shape).
• Examples: Stretched rubber band, a wound-up spring in a toy car, or a bent bow (elastic potential energy).
• Gravitational Potential Energy:
  • Energy gained by an object when raised to a height against gravity.
  • Formula: E_p = mgh (where m is mass, g is acceleration due to gravity, and h is height).
  • Path Independence: The work done by gravity depends only on the difference in vertical height between the initial and final positions, not on the path taken.

Law of Conservation of Energy

• The Law: Energy can neither be created nor destroyed; it can only be converted from one form to another. The total energy before and after the transformation remains the same.
• Mechanical Energy: The sum of kinetic energy and potential energy of an object is constant (assuming no friction).
  Potential Energy + Kinetic Energy = Constant
• Example (Free Fall): As an object falls, its potential energy decreases while its kinetic energy increases by an equal amount. At any point, mgh + ½mv² is constant.

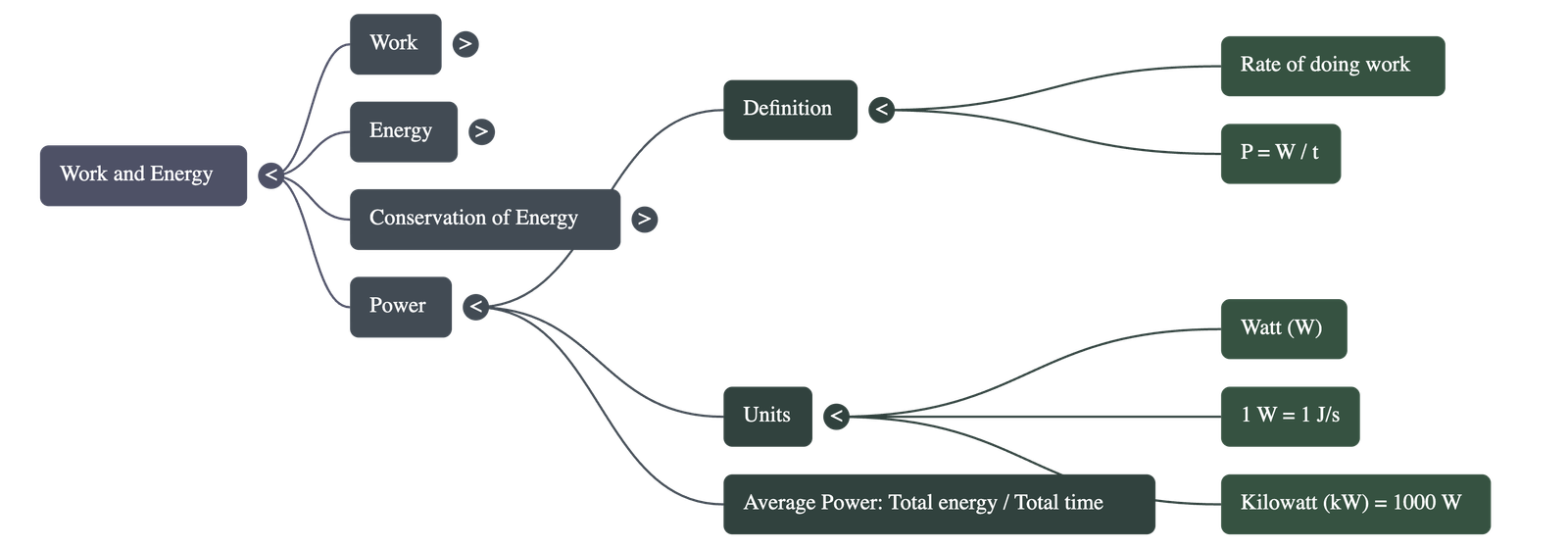
10.3 Rate of Doing Work (Power)

• Definition: Power measures the speed of work done, or the rate of transfer of energy. It determines how fast or slow work is done.
• Formula:
  
  Power = Work / Time (P = W / t)
• Unit: The SI unit is the Watt (W).
  1 Watt = 1 Joule per second (1 J s^-1).
• Larger Units: Kilowatt (kW).
  1 kW = 1000 W = 1000 J s^-1.
• Average Power: When an agent does work at different rates at different intervals, average power is calculated by dividing total energy consumed by total time taken.